Розглянемо деяку ЛДС (див. рис. 4.1), на вході якої діє дискретний випадковий процес 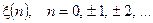 , де
, де 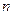 - нормований відносно інтервалу дискретизації час. Відомі розподіли ймовірностей вхідного процесу
- нормований відносно інтервалу дискретизації час. Відомі розподіли ймовірностей вхідного процесу 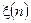 та імпульсна характеристика
та імпульсна характеристика

Рис. 4.1. Лінійна дискретна система
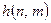 ЛДС. Потрібно знайти моментні функції (математичне сподівання, дисперсію, кореляційну функцію) процесу на виході
ЛДС. Потрібно знайти моментні функції (математичне сподівання, дисперсію, кореляційну функцію) процесу на виході 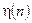 . Таке дослідження процесу на виході ЛДС називають аналізом в рамках кореляційної теорії.
. Таке дослідження процесу на виході ЛДС називають аналізом в рамках кореляційної теорії.
Математичне сподівання відгуку. Спочатку розглянемо знаходження математичного сподівання процесу на виході ЛДС. Скориставшись результатами підрозділу 3.2, формально можемо записати для відгуку ЛДС
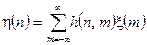 . (4.1)
. (4.1)
Візьмемо тепер математичне сподівання лівої і правої частин співвідношення (4.1). Маємо
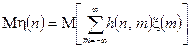 .
.
Враховуючи властивості математичного сподівання, зокрема, його адитивність, можемо поміняти місцями знак суми і математичного сподівання. Тоді
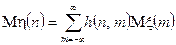 .
.
Введемо позначення для математичних сподівань: 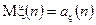 і
і 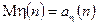 . Тепер остаточно запишемо
. Тепер остаточно запишемо
 (4.2)
(4.2)
|
|
|
Отже, згідно зі співвідношенням (4.2), математичне сподівання відгуку ЛДС у певний момент часу 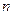 дорівнює зваженій сумі значень математичного сподівання вхідного процесу. Роль вагових коефіцієнтів відіграють відповідні значення імпульсної характеристики ЛДС.
дорівнює зваженій сумі значень математичного сподівання вхідного процесу. Роль вагових коефіцієнтів відіграють відповідні значення імпульсної характеристики ЛДС.
Зазначимо, що згідно з умовою фізичної можливості (див. п. 3.2) 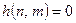 коли
коли 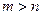 . Тому в (4.2) всі доданки з
. Тому в (4.2) всі доданки з 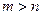 дорівнюють нулеві, тобто можна записати
дорівнюють нулеві, тобто можна записати
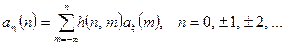 (4.3)
(4.3)
Приклад 4.1. На нерекурсивну ЛДС з імпульсною характеристикою
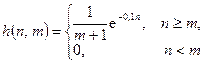
діє дискретній випадковий сигнал 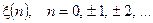 математичне сподівання якого
математичне сподівання якого 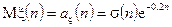 , де
, де 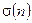 - дискретний одиничний стрибок (див. формулу (3.11)). Знайти математичне сподівання
- дискретний одиничний стрибок (див. формулу (3.11)). Знайти математичне сподівання 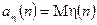 , де
, де 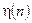 - процес на виході ЛДС.
- процес на виході ЛДС.
Згідно з умовою задачі та формулою (4.3) можемо записати
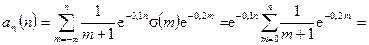
Якщо ЛДС є стаціонарною, тобто коефіцієнти різницевого рівняння не залежать від часу, то її імпульсна характеристика залежить лише від одного дискретного часового аргументу 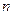 (див. рис. 4.2) і тоді співвідношення (4.1) запишеться у такому вигляді:
(див. рис. 4.2) і тоді співвідношення (4.1) запишеться у такому вигляді:
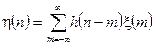 . (4.4)
. (4.4)
Тоді, розмірковуючи аналогічно, для математичного сподівання запишемо
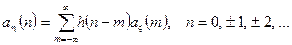 (4.5)
(4.5)
Таким чином, для стаціонарної ЛДС математичне сподівання відгуку на її виході при дії на вході випадкового процесу представляє собою дискретну згортку імпульсної характеристики системи і математичного сподівання впливу.

Рис. 4.2. Стаціонарна лінійна дискретна система
Для фізично існуючих стаціонарних ЛДС імпульсна характеристика 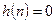 коли
коли 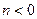 , тому (4.5) можна записати так:
, тому (4.5) можна записати так:
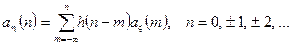 (4.6)
(4.6)
Приклад 4.2.
Для випадкових дискретних сигналів, що існують лише на додатній вісі, тобто мають вигляд 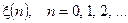 співвідношення (4.3) і (4.6) можна записати так:
співвідношення (4.3) і (4.6) можна записати так:
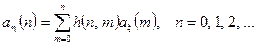
і
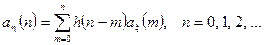
Кореляційна функція відгуку ЛДС. Перейдемо тепер безпосередньо до розгляду кореляційної функції процесу на виході ЛДС. При цьому дисперсію зможемо знайти як частинний випадок кореляційної функції коли зсув між значеннями відгуку дорівнює нулеві.
|
|
|
Оскільки при знаходженні кореляційної функції випадкового процесу використовується процедура центрування останнього, то спершу розглянемо представлення центрованого процесу на виході ЛДС. Центрований дискретний процес на виході ЛДС позначимо так:
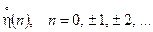 ,
,
де 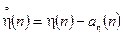 . Тепер, використовуючи співвідношення (4.1) і (4.2), можемо записати
. Тепер, використовуючи співвідношення (4.1) і (4.2), можемо записати
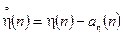 =
=
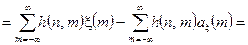
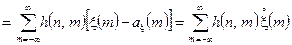 , (4.7)
, (4.7)
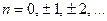 ,
,
де позначено центрований вхідний процес 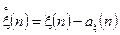 .
.
Отже при проходженні через ЛДС центрованого процесу на виході також отримаємо центрований випадковий процес. Іншими словами, якщо на вході ЛДС діє випадковий процес з нульовим математичним сподіванням, то і на виході отримаємо процес з нульовим математичним сподіванням.
Тоді, враховуючи означення, наведені в п. 2 і співвідношення (4.7), можемо записати для кореляційної функції відгуку ЛДС
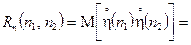
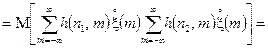
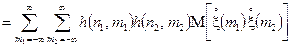 .
.
Зазначимо тепер, що
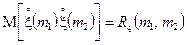
є кореляційна функція процесу на вході ЛДС. Враховуючи це, остаточно отримаємо
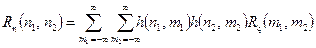 , (4.8)
, (4.8)
Таким чином, кореляційна функція процесу на виході ЛДС повністю визначається кореляційною функцією процесу на вході та імпульсною характеристикою системи.
Приклад 4.3.
Розглянемо тепер стаціонарну ЛДС. Тоді, оскільки для такої системи імпульсна характеристика не залежить від моменту подачі тестую чого одиничного імпульсу (див. п. 3), для кореляційної функції отримаємо
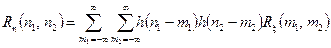 , (4.9)
, (4.9)
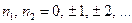
Аналогічно, як і для математичного сподівання, з урахуванням умов фізичної можливості ЛДС в термінах імпульсної характеристики, нескінченні верхні межі підсумовування в правих частинах співвідношень (4.8) і (4.9) можуть бути замінені на поточні значення нормованих часових аргументів кореляційних функцій, тобто
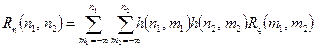 , (4.10)
, (4.10)
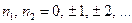 ,
,
для нестаціонарних ЛДС, і
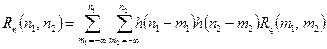 , (4.11)
, (4.11)
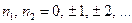 ,
,
для стаціонарних ЛДС.
Приклад 4.4.
Для дискретного випадкового сигналу, що починається у момент часу 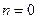 , тобто відмінний від нуля лише на додатній вісі, обчислення кореляційних функцій відгуків фізично існуючих ЛДС (нестаціонарних і стаціонарних відповідно) виконується за наступними виразами:
, тобто відмінний від нуля лише на додатній вісі, обчислення кореляційних функцій відгуків фізично існуючих ЛДС (нестаціонарних і стаціонарних відповідно) виконується за наступними виразами:
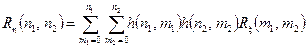 , (4.12)
, (4.12)
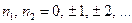 ,
,
і
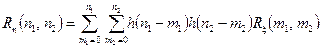 , (4.13)
, (4.13)
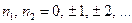 ,
,
Нагадаємо тепер, що коли для кореляційної функції 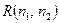 деякого дискретного процесу покласти
деякого дискретного процесу покласти 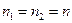 , то отримуємо дисперсію цього процесу
, то отримуємо дисперсію цього процесу 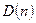 . Таким чином, використовуючи отримані вище вирази (4.8) – (4.13) для кореляційної функції, можемо записати співвідношення для дисперсії відгуку ЛДС. Так, для нестаціонарної ЛДС дисперсія процесу на виході
. Таким чином, використовуючи отримані вище вирази (4.8) – (4.13) для кореляційної функції, можемо записати співвідношення для дисперсії відгуку ЛДС. Так, для нестаціонарної ЛДС дисперсія процесу на виході
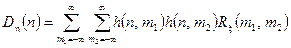 , (4.14)
, (4.14)
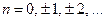
Співвідношення (4.14) вказує на те, що значення дисперсії 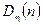 відгуку ЛДС у будь-який момент часу
відгуку ЛДС у будь-який момент часу 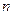 є зваженою сумою не лише значень дисперсії вхідного процесу
є зваженою сумою не лише значень дисперсії вхідного процесу 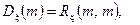
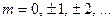 , а і значень кореляційної функції впливу
, а і значень кореляційної функції впливу 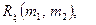 коли
коли 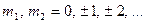 але
але 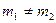 . При цьому роль вагових коефіцієнтів відіграють відповідні значення імпульсної характеристики ЛДС.
. При цьому роль вагових коефіцієнтів відіграють відповідні значення імпульсної характеристики ЛДС.
Приклад 4.5.
У разі стаціонарності ЛДС співвідношення для дисперсії відгуку отримаємо із формули (4.9)
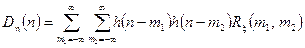 , (4.15)
, (4.15)
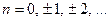
З урахуванням умов фізичної можливості, тобто, коли ЛДС при формуванні сигналу на виході «враховує» лише нинішні та минулі значення вхідного процесу і «не враховує» майбутні значення, формули (4.14) і (4.15) запишуться відповідно так:
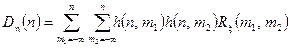 ,
, 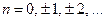
і
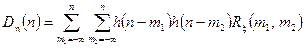 ,
, 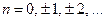
Приклад 4.6.
Ці ж формули для дискретного випадкового сигналу, що відмінний від нуля лише на додатній вісі набудуть такого вигляду:
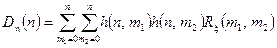 ,
, 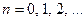
для нестаціонарної ЛДС і
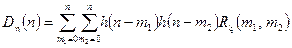 ,
, 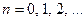
 2015-07-04
2015-07-04 457
457








