Учебно-исследовательское задание

1. Распределения Пирсона [2], их свойства и применения.

2. Броуновское движение в работах А.Эйнштейна и П.Ланжевена [4].

Литература

1. Боровков А.А. Курс теории вероятностей. М: Наука, 1972.

2. В.И.Тихонов. Статистическая радиотехника. М.: Радио и Связь, 1982.

3. В.Т.Горяинов, А.Г.Журавлев, В.И.Тихонов. Статистическая радиотехника. Примеры и задачи. М.: Сов.Радио, 1980.

4. К.В.Гардинер. Стохастические методы в естественных науках. М.:Мир, 1986.

Практическое занятие 5.

Тема: КОНТРОЛЬНАЯ РАБОТА

Практическое занятие 6.

Тема 5: Многомерные случайные величины и условные функции распределения.

Определения и глоссарий

Совместная функция распределения, Многомерные плотности распределения, Условия согласованности для плотностей распределения, Коэффициент корреляции, Моменты распределения, Независимость, некоррелированность, ортогональность случайных величин, Условные плотности и правила исключения лишних переменных в них, Многомерные характеристические функции.

Задания для предварительной самостоятельной подготовки

1. Уяснить взаимоотношение понятий независимости, некоррелированности и ортогональности случайных величин.

2. Уяснить свойства многомерных функций распределения, плотностей распределения и характеристических функций.

Задачи

1. Дискретная двумерная случайная величина (Х,Y) описывается законом распределения вероятностей, заданного таблицей.

уj	xi
	x1	x2
у1 у2 у3	0,10 0,15 0,20	0,15 0,25 0,15

Определить: 1) законы распределения составляющих Х и Y; 2) условный закон распределения случайной величины Х при условии, что Y приняла значение у₁, и случайной величины Y при условии, что Х приняла значение х₂.

2. Вычислить и построить двумерную функцию распределения F₂(х, у) независимых дискретных случайных величин Х и Y, если случайная величина Х принимает три возможных значения 0, 1, 3 с вероятностями 1/2, 2/8 и 1/8, а Y - два возможных значения 0 и 1 с вероятностями 1/3 и 2/3.

3. Случайная точка на плоскости распределена по закону, приведенному в таблице

yj	xi
	x1=0	x2=1
y1=-1	0,10	0,15
y2=0	0,15	0,25
y3=1	0,20	0,15

Найти: 1) математические ожидания случайных величин Х и Y; 2) дисперсии величин Х и Y; 3)условное математическое ожидание величины Х при Y=у₃; 4) корреляционный момент К_ху и коэффициент корреляции R_xy.

4. Производится N независимых измерений некоторой случайной величины. Считая результат каждого измерения случайной величиной с математическим ожиданием m и дисперсией s², вычислить математическое ожидание M и дисперсию D среднего арифметического N измерений.

5. Доказать соотношения: для любых случайных величин X и Y

a. M(X±Y)=M(X)±M(Y)

b. M(XY)=M(X)*M(Y)+K_XY

c. D(X±Y)=D(X)+D(Y)±2K_XY

6. Совместная плотность вероятности р₂(х,y) гауссовского распределения двумерной случайной величины (Х,Y) имеет вид:

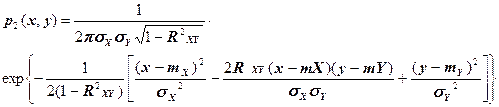
Определить одномерные плотности вероятности случайных величин X и Y и условные плотности p(x|y), p(y|x).

7. Пользуясь понятием условной плотности распределения и одномерной плотностью распределения гармонического процесса 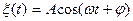с постоянной амплитудой и угловой частотой 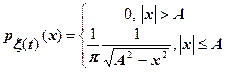, найти двумерную плотность распределения этого процесса.

8. Два гауссовских некоррелированных случайных процесса имеют заданные постоянные математические ожидания и дисперсии. Записать совместную плотность распределения вероятностей этих процессов.

9. Имеется два случайных процесса 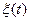и 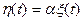, где α - постоянный коэффициент. Считая 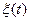гауссовским с нулевым математическим ожиданием и дисперсией 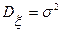, и используя определение условной вероятности, записать совместную плотность распределения 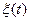и .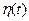

10. Совместная плотность вероятности p₂(x,y) двумерной случайной величины (Х,Y) имеет вид 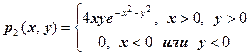. Найти математические ожидания и дисперсии случайных величин Х и Y.