Определение 8.4

Случайная величина X называется непрерывной, если ее функция распределения F(х) = Р(Х < х) непрерывна.

Плотность распределения f(x) должна удовлетворять двум условиям:

а) плотность распределения любой случайной величины неотрицательна:

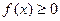(8.3)

Это свойство вытекает из того, что производная неубывающей функции f(х) = F'(х) неотрицательна, а функция распределения F(х) — функция, не убывающая по определению;

б) интеграл от плотности f(х) по всему интервалу (a, b) равен 1:

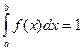(8.4)

Функция распределения F(х) и плотность распределения f(x) обладают следующими свойствами:

1. Функция распределения случайной величины Х равна вероятности (по определению), значит, ее значения заключены в интервале от 0 до 1:

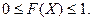(8.5)

2. F(х) — неубывающая функция по ее определению, т.е. F(х₂) > F(х₁), если х₂ > х₁.

3. Если функция распределения непрерывна, то вероятность любого отдельного значения х_i случайной величины равна нулю при этом значении:

Р(Х = х₁) = 0,

если F(Х) непрерывна в точке X = х_i.

4. Вероятность попадания случайной величины X в интервал от α до β равна приращению функции распределения на концах этого интервала:

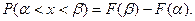(8.6)

Учитывая свойство 3, можем записать следующее равенство:

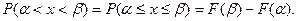(8.7)

То есть вероятность попадания непрерывной случайной величины в открытый интервал равна вероятности ее попадания в замкнутый интервал.

5. Вероятность попадания случайной величины X в интервал от α до β может определяться плотностью вероятностей:

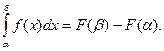(8.8)

6. Функция распределения удовлетворяет условиям:

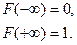(8.9)

7. Несобственный интеграл от дифференциальной функции в пределах от 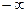до 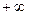равен 1:

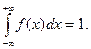(8.10)

8. Функция распределения F(х) выражается через плотность f(x) формулой:

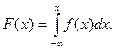(8.11)

Непрерывная случайная величина X опредсляется заданием интервала (a, b), содержащего возможные значения этой величины, и функции f(х). Множество значений X может быть любым интервалом. Возможен даже случай а = 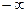_; а также b= .

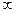Физический смысл плотности распределения f(х) следующий:

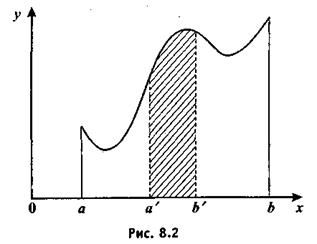
пусть (a’, b’) — произвольный интервал, содержащийся в (a, b) (то есть а<а', b<b'). Тогда вероятность того, что непрерывно распределенная случайная величина Х окажется в интервале (a’, b’), равна определенному интегралу

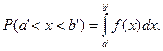(8.12)

или площади криволинейной трапеции, ограниченной сверху графиком функции у =f(х), снизу — осью Ох, а с боковых сторон — прямыми х = а и х = b (рис. 8.2).

График функции y = f(х) называется кривой распределения, или графиком плотности распределения. Кривая y = f(х) располагается над осью абсцисс.