Транспортная задача
1 Понятие транспортной задачи
2 Определение открытой и сбалансированной задачи
3 Причины неэффективности симплекс-метода при решении транспортной задачи
4 Алгоритм приведения открытой транспортной задачи к сбалансированной
5 для любой транспортной задачи существует план
6 транспортная задача всегда имеет оптимальный план
7 любой опорный план транспортной задачи имеет не более n+m-1 положительных компонент
8 оптимальный план содержит не более n+m-1 компонент
Постановка задачи
Имеется целый набор специфических задач, для которых разработаны особые методы решения задач линейного программирования. В качестве примера таких задач мы рассмотрим так называемую транспортную задачу.
Начнем с её содержательной формулировки.
Пусть имеется некоторый однородный продукт, сосредоточенный на m пунктах отправления (складах), так что на i-м складе находится 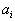 единиц этого продукта.
единиц этого продукта.
Этот продукт необходимо доставить в n пунктов назначения (потребления), причем на j -й пункт необходимо доставить 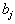 единиц продукта. Запасы и потребности сбалансированы, то есть
единиц продукта. Запасы и потребности сбалансированы, то есть
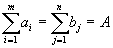 ,
,
то есть наличие продукта равно потребности в нем.
Пусть стоимость перевозки единицы продукта из i -го склада в j- й пункт назначения равна 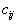 . Пусть
. Пусть 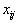 есть то количество продукта, которое перевозится из i -го склада в j -й пункт потребления.
есть то количество продукта, которое перевозится из i -го склада в j -й пункт потребления.
Тогда общие транспортные расходы составят величину
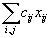 .
.
Из каждого склада весь продукт должен быть вывезен. Это значит, что должно быть выполнено условие
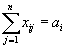 .
.
С другой стороны, потребности j- го пункта назначения должны быть полностью удовлетворены. Это означает, что
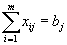 .
.
Желание минимизировать транспортные расходы приводит нас к следующей задаче:
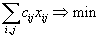
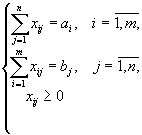
являющейся типичной задачей линейного программирования.
Определение 3.1. Транспортная задача называется открытой транспортной задачей, если условие баланса нарушаются; в случае выполнения условия баланса она называется сбалансированной транспортной задачей.
У этой задачи есть одна очень существенная особенность: в ограничениях перед неизвестными 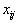 всегда стоит 1. И именно это позволяет разработать гораздо более эффективные и простые алгоритмы решения транспортной задачи, чем симплекс-метод.
всегда стоит 1. И именно это позволяет разработать гораздо более эффективные и простые алгоритмы решения транспортной задачи, чем симплекс-метод.
Сам же симплекс-метод был бы не эффективен по двум причинам:
- Большая размерность решаемой задачи. Общее число неизвестных величин
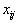 равно mn, и даже при n =m = 10 размерность решаемой задачи уже будет равна 100. Даже ЭВМ будет решать такую задачу симплекс-методом достаточно долго.
равно mn, и даже при n =m = 10 размерность решаемой задачи уже будет равна 100. Даже ЭВМ будет решать такую задачу симплекс-методом достаточно долго. - Опорные планы в транспортной задаче очень часто бывают вырожденными, а наличие вырождения приводит к необходимости несколько модифицировать симплекс-метод.
Приведение открытой транспортной задачи к сбалансированной
- Превышение запасов над потребностями.
В этом случае вводится “фиктивный” 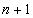 потребитель с потребностями равными абсолютной величине разности между общим количеством запасов и общим количеством требуемых единиц. Стоимость по доставке будет для
потребитель с потребностями равными абсолютной величине разности между общим количеством запасов и общим количеством требуемых единиц. Стоимость по доставке будет для 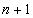 потребителя равна 0, т.к. поставки фактически нет.
потребителя равна 0, т.к. поставки фактически нет.
- Превышение потребностей над запасами.
Вводим “фиктивного” 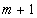 производителя (склад) с потребностями равными абсолютной величине разности между общим количеством запасов и общим количеством требуемых единиц. Стоимость по доставке будет для
производителя (склад) с потребностями равными абсолютной величине разности между общим количеством запасов и общим количеством требуемых единиц. Стоимость по доставке будет для 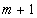 производителя равна 0, т.к. поставки фактически нет.
производителя равна 0, т.к. поставки фактически нет.
2. Простейшие свойства транспортной задачи
Теорема 1. Для любой транспортной задачи существует план (то есть, для любой транспортной задачи допустимая область не пуста).
Доказательство. Действительно, по смыслу задачи, 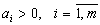
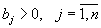 . Так как
. Так как 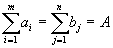 , то возьмем план в виде
, то возьмем план в виде 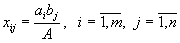 .
.
Величины 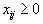 . Далее
. Далее
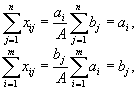
то есть ограничения выполняются. Поэтому 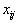 составляют план.
составляют план.
Теорема 2. Транспортная задача всегда имеет оптимальный план.
Доказательство. Действительно, допустимая область не пуста. Далее, так как по смыслу 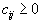 , то для любого плана перевозок
, то для любого плана перевозок
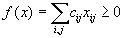 .
.
В силу того, что значения целевой функции ограничены снизу, транспортная задача всегда имеет решение.
Теорема 3. Любой опорный план имеет не более 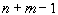 положительных компонент. (Ранг матрицы ограничений равен n+m-1)
положительных компонент. (Ранг матрицы ограничений равен n+m-1)
Доказательство Действительно, исходная система содержит всего 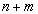 ограничений типа равенств:
ограничений типа равенств:
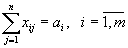 , то есть m ограничений;
, то есть m ограничений;
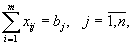 то есть n ограничений.
то есть n ограничений.
Однако в силу соотношения 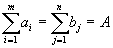 одно из этих ограничений является следствием всех остальных. Действительно, сложим все первые m ограничений
одно из этих ограничений является следствием всех остальных. Действительно, сложим все первые m ограничений
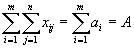
| (1) |
а из второй группы сложим первые n- 1 ограничение
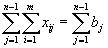
| (2) |
Вычитая теперь (2) из (1), получим:
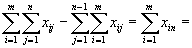
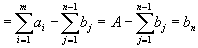 ,
,
и мы получили последнее, n -ое ограничение второй группы.
Таким образом, независимых ограничений всего не более 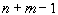 . Поэтому каждый опорный план имеет не более
. Поэтому каждый опорный план имеет не более 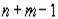 компонент.
компонент.
Следствие. Оптимальный план содержит не более, чем 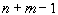 перевозку.
перевозку.
3. Методы определения первоначального опорного плана
3.1. Построение исходного опорного плана (метод северо-западного угла)
Для начала решения транспортной задачи необходимо иметь какой-то исходный опорный план, то есть оказаться в какой-то вершине допустимой области. Приведем конструктивный прием построения такого опорного плана, получивший название "метод северо-западного угла".
Итак, пусть имеется m складов с запасами 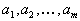 и n пунктов потребления с потребностями
и n пунктов потребления с потребностями 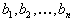 . Пусть запасы и потребности сбалансированы, то есть
. Пусть запасы и потребности сбалансированы, то есть 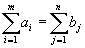 .
.
Представим это в виде таблицы,
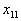
| 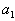
| ||||
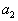
| |||||
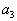
| |||||
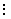
| |||||
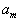
| |||||
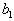
| 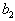
| 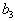
| ... | 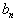
|
где в столбце справа указаны запасы, в строке снизу - потребности, а пустые клетки оставлены для будущего плана перевозок.
Начнем заполнение с клетки, расположенной вверху слева, то есть с "северо-западного угла". Вместо 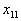 впишем число
впишем число 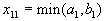 . Возможны два варианта.
. Возможны два варианта.
-
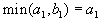 , то есть
, то есть 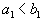 . Тогда, запланировав перевозку из первого склада в первый пункт потребления в объеме
. Тогда, запланировав перевозку из первого склада в первый пункт потребления в объеме 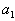 мы полностью опустошим первый склад и там ничего не останется. Поэтому все остальные перевозки из первого склада могут быть только нулевые.
мы полностью опустошим первый склад и там ничего не останется. Поэтому все остальные перевозки из первого склада могут быть только нулевые.
Ну, а потребность в первом пункте потребления останется в объеме 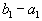 . Наша таблица примет вид:
. Наша таблица примет вид:
| ... | ||||
| |||||
| |||||
| |||||
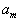
| |||||
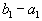
| 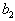
| 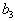
| ... | 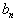
|
Обратите внимание на то, что оставшаяся незаполненной часть таблицы вновь по структуре та же, что и исходная таблица, только в ней на одну строку меньше.
-
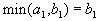 , то есть
, то есть 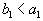 . Тогда, запланировав перевозку из первого склада в первый пункт потребления в объеме
. Тогда, запланировав перевозку из первого склада в первый пункт потребления в объеме 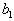 , мы полностью удовлетворим его потребности. Перевозить туда больше будет ничего не надо, поэтому остальные перевозки туда будут равны нулю. Ну, а в первом складе еще останется
, мы полностью удовлетворим его потребности. Перевозить туда больше будет ничего не надо, поэтому остальные перевозки туда будут равны нулю. Ну, а в первом складе еще останется 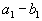 запасов продукта. Наша таблица примет вид:
запасов продукта. Наша таблица примет вид:
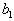
| 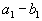
| ||||
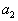
| |||||
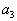
| |||||
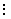
| 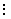
| ||||
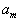
| |||||
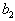
| 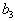
| ... | 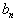
|
Обратите внимание на то, что оставшаяся незаполненной часть таблицы вновь по структуре та же, что и исходная таблица, только в ней на один столбец меньше.
Ну, а дальше все можно повторить, продолжая заполнять оставшуюся часть таблицы перевозок начиная с левого верхнего, "северо-западного" угла, пока не будут исчерпаны запасы всех складов и не удовлетворены потребности всех пунктов потребления.
У нас всего в таблице m строк и n столбцов. Каждый раз исчезает, как минимум, либо строка, либо столбец (могут исчезнуть сразу и строка, и столбец, если запасы какого-то подмножества складов полностью удовлетворят потребности какого-то подмножества пунктов потребления). Однако при последней перевозке исчезает сразу и последняя строка, и последний столбец. Поэтому получающийся план перевозок содержит не более 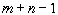 компонент.
компонент.
Мы не будем доказывать, что план, полученный методом северо-западного угла, является опорным. Заметим лишь, что если получающийся план содержит ровно 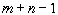 компоненту, то он называется невырожденным. Если число положительных компонент плана перевозок меньше
компоненту, то он называется невырожденным. Если число положительных компонент плана перевозок меньше 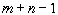 , то он называется вырожденным.
, то он называется вырожденным.
Рассмотрим два примера. С целью экономии места, вся таблица не переписывается, а лишь приписываются последние строки и столбцы.
Пример 1
Пусть 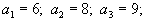
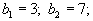
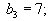
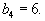
| В данном случае число | ||||||||||
| складов m =3, число пунктов | ||||||||||
| потребления n =4, так что | ||||||||||
| m+n-1=6. Получившийся | ||||||||||
| опорный план содержит ровно | ||||||||||
| 6 компонент, и поэтому являет- | ||||||||||
| ся невырожденным. |
Пример 2
Пусть 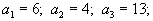
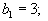
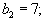
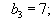
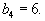 Аналогичная процедура приводит к таблице, изображенной ниже.
Аналогичная процедура приводит к таблице, изображенной ниже.
В этом случае получившийся опорный план имеет всего 5 компонент, то есть является вырожденным. Это
| В данном случае число скла- | ||||||||||
| дов m =3, число пунктов потре- | ||||||||||
| бления n =4, так что m+n-1=6. | ||||||||||
| Получившийся опорный план | ||||||||||
| содержит 5 компонент, и поэтому | ||||||||||
| является вырожденным. |
произошло потому, что запасы складов 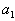 и
и 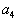 полностью удовлетворили потребности пунктов потребления
полностью удовлетворили потребности пунктов потребления 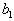 и
и 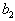 и поэтому в тот момент, когда эти сбалансированные потребности удовлетворились (
и поэтому в тот момент, когда эти сбалансированные потребности удовлетворились (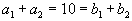 ), обнулились сразу и строка, и столбец.
), обнулились сразу и строка, и столбец.
Ниже вся теория будет строится для случая, когда все опорные планы невырожденные, то есть все они имеют 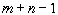 компоненту. Как бороться с явлением вырождения, которое в транспортных задачах встречается достаточно часто - будет рассказано в самом конце.
компоненту. Как бороться с явлением вырождения, которое в транспортных задачах встречается достаточно часто - будет рассказано в самом конце.
3.2. Метод минимального (максимального) элемента
Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел 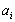 и
и 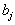 . Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
. Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
Пример № 2
Составить первоначальный опорный план методом минимального элемента для транспортной задачи вида:
Решение:
Задача сбалансирована.
Строим первоначальный опорный план методом минимального элемента.
- Выясним минимальную стоимость перевозок.
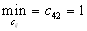 Первая перевозка будет осуществляться с пункта производства
Первая перевозка будет осуществляться с пункта производства 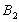 в пункт потребления
в пункт потребления 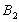 и она составит максимально возможное число единиц продукта
и она составит максимально возможное число единиц продукта 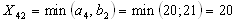 :. В этом случае, потребности пункта потребления
:. В этом случае, потребности пункта потребления 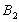 будут удовлетворены полностью. Значит, стоимости столбца 2 можно больше не рассматривать, так как перевозки
будут удовлетворены полностью. Значит, стоимости столбца 2 можно больше не рассматривать, так как перевозки 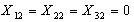 .Выясним минимальную стоимость перевозок (без учета столбца № 2).
.Выясним минимальную стоимость перевозок (без учета столбца № 2).
-
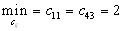 Вторая и третья перевозки будут осуществляться с пункта производства
Вторая и третья перевозки будут осуществляться с пункта производства 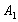 и
и 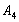 в пункт потребления
в пункт потребления 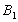 и
и 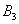 соответственно и составят максимально возможное число единиц продукта:
соответственно и составят максимально возможное число единиц продукта: 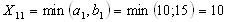 ,
, 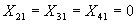 ;
; -
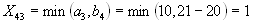
- Четвертая перевозка осуществляется с пункта
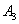 в пункт потребления
в пункт потребления 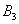 , т.к.
, т.к. 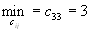 (без учета первого, второго столбца и четвертой строки).
(без учета первого, второго столбца и четвертой строки). 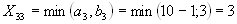 .
. - Пятая перевозка осуществляется с пункта
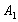 в пункт потребления
в пункт потребления 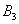 , т.к.
, т.к. 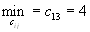 (без учета первого, второго столбца, третьей и четвертой строки).
(без учета первого, второго столбца, третьей и четвертой строки). 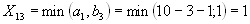 .
.
- Шестая перевозка осуществляется с пункта
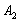 в пункт потребления
в пункт потребления 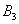 т.к.
т.к. 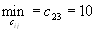 (без учета первого, второго столбца, первой, третьей и четвертой строки).
(без учета первого, второго столбца, первой, третьей и четвертой строки).
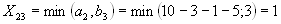
Опорный план имеет вид;
3.3. Метод аппроксимации Фогеля
При определении опорного плана транспортной задачи методом аппроксимации Фогеля находят разность по всем столбцам и по всем строкам между двумя записанными в них минимальными тарифами. Эти разности записывают в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают минимальную. В строке (или в столбце), которой данная разность соответствует, определяют минимальная стоимость.
Если минимальная стоимость одинакова для нескольких клеток столбца (строки), то для заполнения выбирают ту клетку, которая расположена в столбце (строке, соответсующем наибольшей разности между двумя минимальными стоимостями, находящимися в данном столбце (строке).
Пример
Найти методом аппроксимации Фогеля первоначальный опорный план транспортной задачи:
(Здесь мы перенесли потребности в верхнюю строку для удобства построения плана). Рассмотрим задачу, приведенную для методов северо-западного угла и минимального элемента
Решение:
| - | ||||||
| - | - | |||||
| - | ||||||
| - | ||||||
| - | - | |||||
| - | - | - |
Опорный план имеет вид:
.3.4. Метод двойного предпочтения
В случае больших размерностей, эффективен способ определения первоначального опорного плана с помощью метода двойного предпочтения.
В каждом столбце отмечают знаком клетку с наименьшей стоимостью. Затем тоже проделывают в каждой строке. В результате некоторые клетки имеют двойную отметку. В них находится минимальная стоимость как по столбцу, так и по строке. В эти клетки помещают максимально возможные объемы перевозок, каждый раз исключая и рассмотрения соответствующие столбцы или строки. Затем распределяют перевозки по клеткам с единичной отметкой. Остальные перевозки распределяют по наименьшей стоимости.
Пример
| 2** | |||
| 6* | |||
| 3* | |||
| 1* | 2* |
- Заполняем клетки с двойным предпочтением:
- Заполняем клетки с простым предпочтением, начиная с наименьшей стоимости.
3. Заполняем оставшиеся пустыми клетки.
Это опорный план составленный методом двойного предпочтения.
4. Методы проверки опорного плана на оптимальность
4.1. Потенциалы. Критерий оптимальности плана
Итак, наша транспортная задача имеет вид:
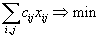
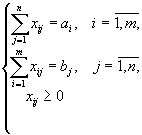
Распишем нашу задачу в векторной форме. Для этого введем векторы
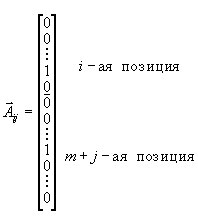
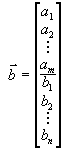
Тогда ограничения задачи (3) могут быть записаны в виде
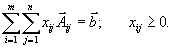
Как уже говорилось выше, одно из этих ограничений является лишним, и оно может быть вычеркнуто.
Рассмотрим теперь двойственную задачу. Так как ограничений всего m + n, то и соответствующие переменные двойственной задачи обозначим так: 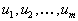 (переменные, соответствующие первым m ограничениям) и
(переменные, соответствующие первым m ограничениям) и 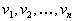 (переменные, соответствующие последним n ограничениям). Тогда, учитывая вид векторов
(переменные, соответствующие последним n ограничениям). Тогда, учитывая вид векторов 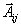 и вид вектора
и вид вектора 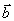 , запишем двойственную задачу в следующем виде:
, запишем двойственную задачу в следующем виде:
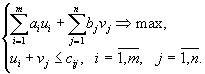
Величины 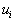 называются потенциалами складов, а величины
называются потенциалами складов, а величины 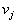 - потенциалами пунктов потребления.
- потенциалами пунктов потребления.
Так как одно из ограничений является лишним, то на самом деле одного из потенциалов нет. Для сохранения симметрии всех формул и обозначений можно просто полагать, скажем, 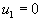 .
.
Пусть теперь 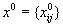 - оптимальный опорный план транспортной задачи. Тогда, согласно теореме двойственности, должно выполняться условие
- оптимальный опорный план транспортной задачи. Тогда, согласно теореме двойственности, должно выполняться условие
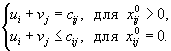
Это и позволяет проверить оптимальность любого опорного плана.
Сам алгоритм выглядит следующим образом:
- Один из потенциалов задается произвольно, скажем, полагается
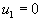 .
. - Рассматривается система линейных уравнений вида
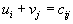 для тех наборов индексов i, j, для которых
для тех наборов индексов i, j, для которых 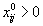 , и находятся потенциалы
, и находятся потенциалы 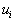 и
и 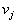 всех складов и всех пунктов потребления.
всех складов и всех пунктов потребления. - Для всех остальных наборов индексов i, j (для которых
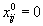 ) проверяется условие
) проверяется условие 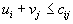 .
.
Если это условие выполняется для всех наборов индексов i, j, для которых 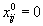 , то рассматриваемый план является оптимальным. Если же, хотя бы для одной пары
, то рассматриваемый план является оптимальным. Если же, хотя бы для одной пары 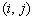
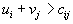 , то план не оптимален.
, то план не оптимален.
Прежде, чем приводить пример, расскажем о том, как реализуется пункт 2 этого алгоритма, когда находятся потенциалы 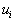 и
и 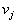 . Обычно он реализуется следующим образом:
. Обычно он реализуется следующим образом:
- Одна из величин
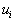 или
или 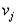 задается произвольно, например, полагается
задается произвольно, например, полагается 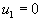 .
. - Затем рассматриваются уравнения вида
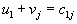 для тех j, для которых
для тех j, для которых 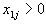 . Так как
. Так как 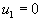 известно, то находятся
известно, то находятся 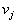 для некоторого множества индексов
для некоторого множества индексов 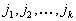 .
. - Для этих индексов
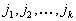 рассматриваются уравнения вида:
рассматриваются уравнения вида: 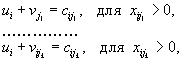
для тех 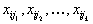 , которые больше нуля. Так как
, которые больше нуля. Так как 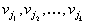 известны, тот находятся величины
известны, тот находятся величины 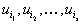 для некоторого множества индексов
для некоторого множества индексов 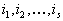 .
.
4. Далее повторяются пункты 2 (движение по строкам) и 3 (движение по столбцам), пока не определятся все потенциалы.
Проиллюстрируем этот процесс примером, а заодно покажем форму записи результатов при ручном счете.
Пример
Пусть имеется три склада с запасами 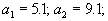
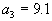 и четыре пункта потребления с потребностями
и четыре пункта потребления с потребностями 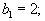
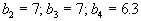 . Коэффициенты
. Коэффициенты 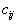 , определяющие стоимость перевозок, заданы матрицей:
, определяющие стоимость перевозок, заданы матрицей:
Таблица стоимостей перевозок
| Пункты потребления | ||||
| Ск | ||||
| ла | ||||
| ды |
Построим исходный опорный план методом северо-западного угла. Он имеет вид
| 3.1 | |||
| 3.9 | 4.2 | ||
| 2.8 | 6.3 |
План имеет 6=3+4-1 компонент, поэтому он является невырожденным. Заметим, что для него транспортные расходы равны 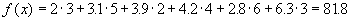 .
.
Заготовим матрицу размером 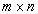 (в нашем случае размером 3´ 4), в которую впишем те коэффициенты
(в нашем случае размером 3´ 4), в которую впишем те коэффициенты 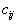 , которые соответствуют ненулевым перевозкам нашего плана (смотрите следующую страницу).
, которые соответствуют ненулевым перевозкам нашего плана (смотрите следующую страницу).
Далее действуем следующим образом:
- Полагаем
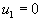
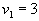
| 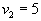
| 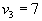
| 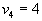
| |
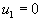
| ||||
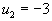
| ||||
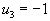
|
2. Идем по строке.
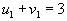 , следовательно , следовательно 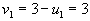 ; ;
|
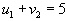 , следовательно , следовательно 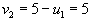 . .
|
- Идем по столбцу.
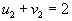 , следовательно , следовательно 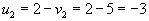 . .
|
- Идем по строке.
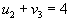 , следовательно , следовательно 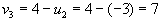 . .
|
- Идем по столбцу.
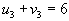 , следовательно , следовательно 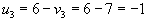 . .
|
- Идем по строке.
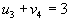 , следовательно , следовательно 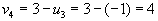 . .
|
Таким образом, определились потенциалы всех пунктов - и складов и пунктов потребления. Теперь можно закончить заполнение этой таблицы, вписав в пустые клетки суммы 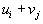 , то есть суммы соответствующих потенциалов. В результате получим:
, то есть суммы соответствующих потенциалов. В результате получим:
| 7 | ||||
| -3 | ||||
| 2 |
В ней жирным шрифтом помечены те 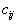 , которые использовались для нахождения потенциалов.
, которые использовались для нахождения потенциалов.
Сравнивая с матрицей величин 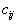 мы видим, что условие оптимальности плана
мы видим, что условие оптимальности плана 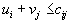 нарушено в двух местах - для
нарушено в двух местах - для 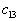 и
и 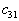 . Следовательно, построенный нами план перевозок не является оптимальным.
. Следовательно, построенный нами план перевозок не является оптимальным.
 2015-07-03
2015-07-03 1159
1159








