Прочность при растяжении КМ, армированных дискретными волокнами

Критическая длина волокон.

Рассмотренные в § 5 формулы для определения прочности КМ справедливы лишь тогда, когда армирующие волокна непрерывны. Если же КМ армирован короткими (дискретными) во­локнами, следует учитывать так называемый «концевой эффект», связанный с концентрацией напряжений у кон­цов волокон, который сказывается на величине проч­ности КМ в целом.

В КМ, армированном параллельно уложенными короткими волокнами длиной l и нагруженном вдоль волокон, нагрузка передается волокнам за счет касатель­ных напряжений на поверхностях раздела между волок­нами и матрицей. В зависимости от длины волокон воз­можны два случая поведения их в КМ. При значениях l, меньших определенной критической длины l _кр, растягивающие напря­жения в волокнах ока­зываются недостаточны­ми для того, чтобы вы­звать их разрушение, волокна вытягиваются из матрицы и прочность их недоиспользуется.

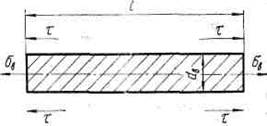
Рис. 12. Силы, действующие на волокно при растяжении армированной композиции

При l > l _кр волокна разрушаются от растягивающих напряжений, при этом, чем больше l, тем большую прочность имеет КМ в целом.

Критической длиной волокна l _кр называют минимальную длину волокон, при которой они разрушаются в КМ. Величина l _кр зависит от прочности связи между матрицей и волокнами и диаметра волокон. Если приближенно принять, что по длине волокна касательные напряжения распределены равномерно (это близко к поведению КМ с идеально пластичными матрицами), то значение l _кр можно найти из условия равновесия касательных и нормальных сил, действующих на волокно (рис. 12):

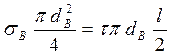(1.55)

Здесь τ – касательные напряжения на границе раздела волокно-матрица;

- нормальные растягивающие напряжения в волокне;

l и 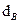- длина и диаметр волокна.

При l=l _кр в момент разрушения КМ касательные напряжения равны сдвиговой прочности границе раздела 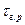, а растягивающие напряжения в волокнах- их пределу прочности 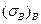, поэтому

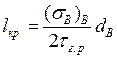(1.56)

Таким образом, критическая длина волокон увеличивается с уменьшением прочности границы раздела и увеличением прочности волокон и их диаметра. В КМ с пластичной матрицей максимальное касательное напряжение на границе раздела может лимитироваться пределом текучести матрицы.

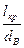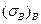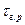Обычно в расчетах используют безразмерную величину , а не абсолютное значение l _кр, поскольку она не зависит от диаметра волокон. Пользуясь формулой (1.56), эту величину можно оценить по известным и . Расчет показывает (табл. 3), что для армированных металлов 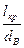лежит в пределах 10-250, для пластиков эта величина может равняться 350 и более.

С повышением температуры величина 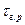уменьшается, поэтому КМ, предназначенные для работы при высоких температурах, должны иметь волокна большей длины, чем низкотемпературные материалы. Точное значение прочности связи между арматурой и матрицей не поддается аналитическому расчету, поэтому его определяют экспериментально.

Таблица 3 Значение 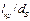для КМ с различной прочностью границы раздела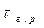 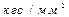и тремя уровнями прочности волокон .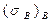

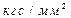Материал матрицы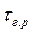
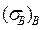
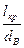
Смола	1,0
Al	1,4
Ag	2,8
Cu, Ni	3,5

Правило смесей для КМ с дискретными волокнами. Расчёт прочности.

Прочность в направлении армирования для КМ, упрочненных параллельными отрезками волокон, можно оценивать по правилу смесей с учетом «концевого эффекта». Рассмотрим, какое влияние оказывает длина волокон на величину среднего растягивающего напряжения 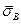в них.

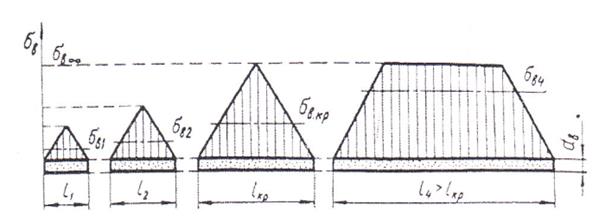
Рис. 13. Эпюры растягивающих напряжений в волокнах различной длины.

1. l < l _кр. В этом случае по мере увеличения длины растет как максимальное растягивающее напряжение (действует посредине волокна), так и среднее растягивающее напряжение 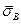в волокнах, которое можно рассчитать по формуле:

.

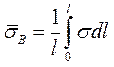Предположим, что нормальные напряжения в волокнах растут к его середине по линейному закону (рис. 13). Тогда при l < l _кр эпюра напряжений имеет вид, изображаемый на волокнах с длинам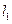и и 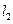. Максимальное напряжение отмечено штриховой линией, среднее- штрих-пунктирной. В этом случае максимальное напряжения в волокнах не достигают их предела прочности и среднее нормальное напряжение

.

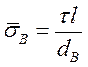Разрушаются такие КМ за счет вытягивания волокон. При этом среднее растягивающее напряжение в волокнах в момент разрушения КМ равно 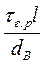и уравнение аддитивности (1.41) принимает вид

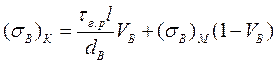(1.57)

Таким образом, если 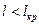, то прочность однонаправленных КМ возрастает пропорционально объемной доле волокон, отношение 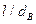, прочности границы раздела и прочности матрицы, оставаясь при этом меньше прочности КМ, армированных непрерывными волокнами.

2. l ≥ l _кр. Когда длина волокна становится равной l _кр, максимальное нормальное напряжение в средней части волокна достигает значения, равного растягивающему напряжению 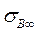в бесконечно длинном волокне. При дальнейшем увеличении l уровень максимального напряжения в волокне остается неизменным (равным 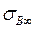), но увеличиваются участки волокон, на которых действует это напряжение. Следовательно, растут и среднее напряжение 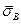, т.е. для волокон длиной 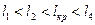имеет место соотношение .

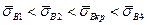Предположим, что величина среднего растягивающего напряжения в волокне на концевых участках длиной 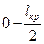равна 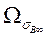, где Ω- коэффициент, меньший 1. Эти участки составляют часть общей доли волокон, равную 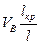. Доля участков, на которых действует напряжение 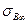, составляет .

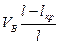Напряжение 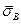, усредненное по всей длине волокон, можно определить следующим образом:

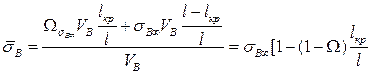] (1.58)

Если растягивающее напряжение от концов волокон растет линейно (рис. 13), то Ω=0,5. Тогда среднее напряжение в волокнах

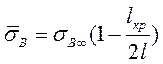. (1.59)

В соответствии с правилом аддитивности общее напряжение, приложенное к КМ, равно сумме средних напряжений в матрице и волокнах. Применительно к КМ с дискретными волокнами, имеющими l > l _кр, можно записать

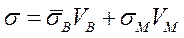. (1.60)

В момент разрушения 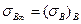, а 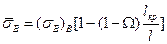. Подставив это значение в уравнение (1.60) и заменив в нем напряжение в матрице 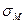напряжением 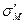,получим формулу для оценки прочности КМ, армированного дискретными волокнами, которая наряду с влиянием объемной доли волокон учитывает и влияние их длины:

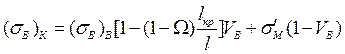(1.61)

Как и при армировании непрерывными волокнами, предел прочности композиции с короткими волокнами растет пропорционально 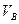, если 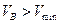. С увеличением отношения 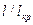прочность КМ возрастает, приближаясь к прочности композиций с непрерывными волокнами ( = ∞).

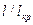Сопоставив между собой уравнения (1.41) и (1.61) и положив в последнем Ω ≈ 0.5, получим соотношение между прочностями КМ, упрочненных дискретными и непрерывными волокнами:

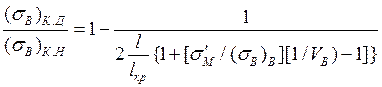(1.62)

Как показывают расчеты, уже при 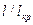= 10 прочность КМ с дискретными волокнами достигает 95 % прочности КМ с непрерывными волокнами. Таким образом, армирование дискретными волокнами позволяет получить практически ту же прочность композиций, что и армирование непрерывными волокнами, если отрезки волокон достаточно длинны.

Минимальную критическую долю дискретных волокон в КМ рассчитывают так же, как и в случае КМ с непрерывными волокнами. Например,

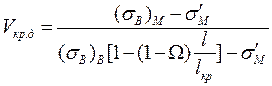(1.63)

Критическая и минимальная доля дискретных волокон всегда больше, чем соответствующее значение для непрерывных волокон. Например, у алюминия, армированного волокнами с , для непрерывных волокон 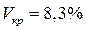, а для дискретных волокон 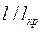= 1 доля .

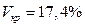ДСП 21.03

2.9. Распределение напряжения по длине волокон..

Анализируя прочность КМ, армированных параллельными дискретными волокнами, мы отметили, что от матрицы к волокну нагрузка передается за счет касательных напряжений τ, действующих на границе раздела. Эти напряжения, как и нормальные напряжения в волокнах, на концах волокна и в средней его части не одинаковы.

Закономерности распределения напряжений вдоль волокон. Разработано несколько моделей, позволяющих установить распределение напряжений. Приводят эти модели к качественно одинаковым результатам, поэтому мы рассмотрим только одну из них, предложенную Б. Розеном.

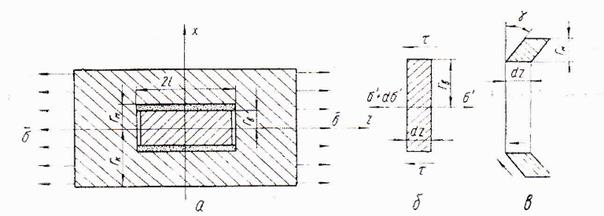
Рис. 14. К расчету распределения напряжений по длине волокна при растяжении однонаправленной композиции с дискретными волокнами: а - модель элемента КМ; б - элементарный отрезок волокна; в -элементарный отрезок матрицы в деформированном состоянии.

Модель (рис. 14,а) представляет собой волокно радиусом 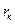и длиной 2 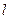, жестко связанное с тонким цилиндрическим слоем матричного материала радиусом 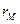, который в свою очередь окружен оболочкой радиусом 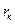из материала с осредненными свойствами композиции. Пусть ось волокна совпадает с осью z, а ось х проходит перпендикулярно к ней через середину волокна. Предполагается, что волокна несут только нормальные напряжения 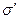, а матричный слой- только касательные напряжения τ, которые в этом слое локализуются, а в оболочке с осредненными свойствами композиции отсутствуют. Нагружена модель внешним напряжением 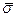, параллельным оси волокон, при этом торцы волокна в передаче напряжений участия не принимают.

Выделим элементарный отрезок волокна длиной dz (рис. 14,б) и запишем условия равновесия сил, действующих на него. Этот отрезок нагружен касательными напряжениями τ по периферии и нормальными 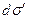по торцам. Суммарная сдвиговая нагрузка, действующая на него, равна 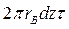, а суммарная нормальная- 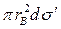. Условие равновесия запишется так:

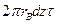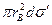+ =0,

или

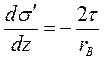. (1.64)

Условие равновесия сил, действующих на всю модель в направлении оси z, при условии, что матрица нормальных нагрузок не несет, можно записать в виде

,

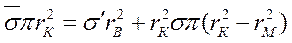или

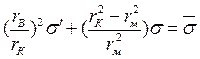, (1.65)

где 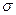-нормальное напряжение в «осредненном» КМ.

Под действием касательных напряжений τ матричный слой вместе с ним «осредненный» КМ сдвигаются по отношению к волокну. Для элементарного отрезка матрицы (рис. 14, в) величину тангенса угла сдвига можно выразить как

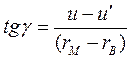, (1.66)

где 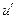- осевое перемещение волокна; u – осевое перемещение «осредненного» материала.

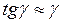Предположим, что волокно, матрица и «осредненный» материал деформируются упруго и, следовательно, подчиняются закону Гука. В силу малости угла γ можно считать, что , и записать

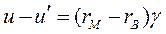. (1.67)

Продифференцируем обе части равенства (1.67) по z, учитывая при этом известные из сопротивления материалов соотношения 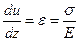и 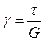, где ε- относительная деформация, Е и G – модули нормальной упругости и сдвига. Тогда получим

,

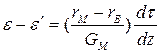или

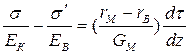. (1.68)

Здесь ε и 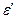- относительные линейные деформации «осредненного» материала и волокна, соответственно; 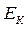и 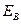- модули Юнга «осредненного» КМ и волокна; 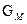- модуль сдвига матрицы.

Продифференцировав еще раз по z уравнение (1.68), получаем

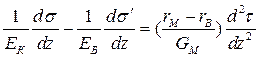. (1.69)

Если продифференцируем по z уравнение (1.65), то получим

,

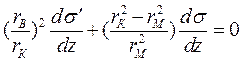или

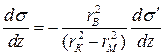. (1.70)

Подставив в уравнение (1.69) вместо 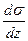выражение (1.70), а вместо выражение (1.64), приходим к дифференциальному уравнению относительно касательных напряжений τ:

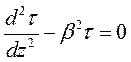, (1.71)

где

. (1.72)

Решение уравнения (1.71) имеет вид

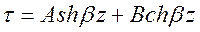. (1.73)

Используя граничные условия: τ =0 при z =0 и 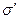=0 при z = l (начало координат находится в середине волокна), приходим к уравнениям, устанавливающим зависимость касательных и нормальных напряжений от координаты z:

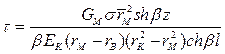; (1.74)

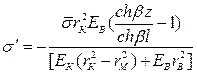. (1.75)

Нормальные напряжения 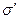в волокне увеличиваются от концов волокна к его середине, достигая при z =0 максимального значения

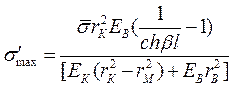. (1.76)

Касательные напряжения имеют наибольшую величину на конце волокна (при z = l) и уменьшаются до нуля в его середине (при z =0). Эпюры нормальных и касательных напряжений представлены на рис. 15.

Если принять, что 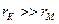, то безразмерный параметр

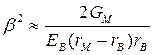(1.77)

и тогда уравнения (1.74) и (1.75) можно привести к виду

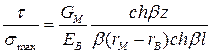(1.78)

и

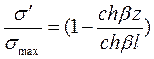, (1.79)

где 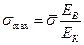- максимальное нормальное напряжение в бесконечно длинном волокне.

Если матрица проявляет пластические свойства, то концентрация касательных напряжений у концов волокна уменьшается, однако характер изменения напряжений по длине волокна остается тем же.

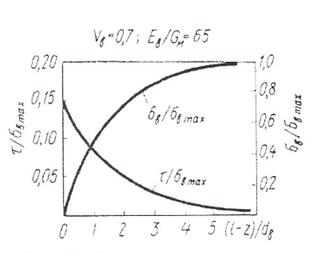
Рис.15.Распределение нормальных и касательных напряжений по длине

волокна при растяжении КМ, содержащего 70% волокон.

Неэффективная длина волокон. Поскольку нормальные напряжения у концов малы, волокна здесь оказываются недогруженными. В результате часть волокна «неэффективна» как элемент, несущий нагрузку. Длина этой части зависит от соотношения упругих свойств матрицы и волокон, от геометрических параметров модели.

Неэффективно нагруженные участки волокон имеются и при растяжении КМ с непрерывной арматурой. Обычно волокна обладают существенным разбросом прочности и часть из них разрушается даже при сравнительно низких напряжениях. У концов разрушившихся волокон напряжения распределяются примерно так же, как у концов дискретных волокон, поэтому концы сломанных волокон не создают упрочнения т.е оказываются неэффективными. Точно определить размер неэффективной части волокна нельзя: это понятие условное полезное при рассмотрении статистической модели прочности КМ.

Условимся называть неэффективной длиной волокна l* такое расстояние от его конца, на котором растягивающее напряжение 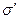в волокне достигает определенной, наперед заданной части напряжения в бесконечно длинном волокне 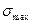. Иными словами, в конце неэффективного отрезка волокна

,

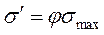где φ – коэффициент, меньший 1;обычно считают разумным φ≈0,9.

Если в уравнение (1.79) положить 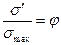; 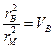и решить его относительно z (при этом z = l*), получим

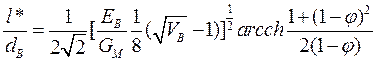. (1.80)

Чтобы волокна были нагружены эффективно (напряжение в их середине превышает 0,9 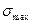), нужно их длину брать большей 2 l*, поскольку неэффективные участки существуют у обоих концов. Эффективный участок в этом случае – отрезок длиной L-2 l*, где L – общая длина волокна. С увеличением L эффективность армирования увеличивается. При упруго- пластическом поведении матрицы неэффективная длина волокна больше, чем при чисто упругом.