2015-07-21
263
При обработке результатов измерений рекомендуется следующая последовательность операций.
5.1. Вычисление среднего арифметического значения из n измерений (n = 2 -- 10).
,
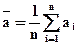где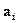 
- результат отдельного измерения.
5.2. Нахождение погрешности отдельных измерений
.
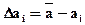5..3. Нахождение среднеквадратической погрешности измерений
.
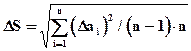5.4. Значение достоверности результата серии измерений задается доверительной вероятностью Рs означающей, что истинное значение измеряемой величины попадает в данный доверительный интервал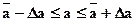 
(например, принимаем Ps = 0,95).
5.5. Определение коэффициента Стьюдента Ts (табл. 4) для принятой доверительной вероятности (Ps = 0,95) и числа проведенных измерений, например, n = 6; Ps = 2,57.
Таблица 4
| Коэффициенты СтьюдентаTs | |||||
| Число измерений | Вероятность Ps | ||||
| n | 0,90 | 0,95 | 0,98 | 0,99 | 0,999 |
| 6,31 | 12,7 | 31,6 | 63,7 | 636,6 | |
| 2,02 | 2,57 | 3,36 | 4,03 | 6,86 | |
| 1,83 | 2,26 | 2,82 | 3,25 | 4,78 | |
| 1,73 | 2,09 | 2,72 | 2,86 | 3,88 |
Нахождение границы доверительного интервала (погрешность результата измерений)
.
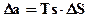5.7. Окончательный результат:
|
|
|
.
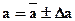5.8. Нахождение относительной погрешности:
.
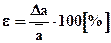5.9 Определение основной погрешности манометра производится по формуле:
,
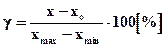где X -измеренное манометром значение;
Xo - действительное значение параметра;
Xmax - максимальное значение шкалы прибора;
Xmin - минимальное значение шкалы прибора.
