Будем теперь рассматривать спин, находящийся во внешнем постоянном однородном магнитном поле. Взаимодействие магнитного момента с полем в соответствии с классическим выражением для энергии (1.5) должно описываться гамильтонианом
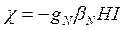 (1.24а)
(1.24а)
для ядерных спинов и
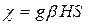 (1.25б)
(1.25б)
для электронных спинов. Гамильтонианы вида (1.24) называются спин-гамильтонианами, так как в них участвуют только спиновые переменные. Взаимодействие спинов с магнитным полем вида (1.24) называется часто зеемановским взаимодействием спинов.
Введем систему координат. Пусть магнитное поле направлено вдоль оси Z этой системы. Тогда вместо (1.21) имеем
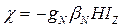 (1.25а)
(1.25а)
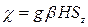 (1.25б)
(1.25б)
Для определенности далее в этом разделе будем рассматривать электронные спины. Гамильтониан (1.25б) имеет два собственных значения (для уровня энергии) и две собственные волновые функции. В отсутствие магнитного поля имелось вырождение по проекции спина. В магнитном поле, как можно увидеть из (1.25), это вырождение снимается: происходит расщепление уровней. Графически это можно изобразить следующим образом (рис. 2)
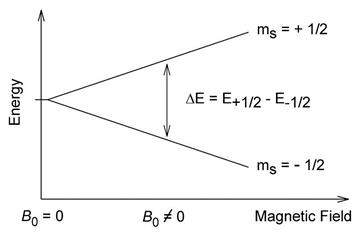
Рис. 2.
При воздействии зависящего от времени возмущения между уровнями могут происходить переходы. Согласно квантовомеханической теории возмущений, вероятность перехода между состояниями а и b при воздействии зависящего от времени гармонического возмущения с гамильтонианом 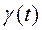 = 2 F
= 2 F 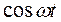 есть
есть
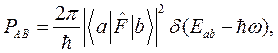 (1.26)
(1.26)
где 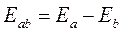 есть разность энергий между двумя состояниями. Из (1.26) следует, что переход возможен только при выполнении условия
есть разность энергий между двумя состояниями. Из (1.26) следует, что переход возможен только при выполнении условия 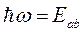 . Такие переходы называются резонансными. Для рассматриваемой спиновой системы это условие выглядит как
. Такие переходы называются резонансными. Для рассматриваемой спиновой системы это условие выглядит как
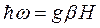 . (1.27)
. (1.27)
Так как магнитный момент взаимодействует с магнитным полем, то зависящее от времени возмущение должно быть переменным магнитным полем. Мы будем обозначать везде создаваемое спектрометром переменное магнитное поле как Н1. Тогда
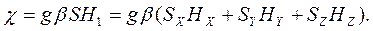 (1.28)
(1.28)
Чтобы матричный элемент этого оператора между состояниями 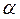 и
и 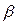 был отличен от нуля, необходимо, чтобы Н1 было перпендикулярно оси Z (так как
был отличен от нуля, необходимо, чтобы Н1 было перпендикулярно оси Z (так как 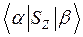 =0). Пусть для определенности Н1 параллельно оси Х. Так как
=0). Пусть для определенности Н1 параллельно оси Х. Так как 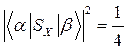 , вероятность перехода (1.26) принимает вид
, вероятность перехода (1.26) принимает вид
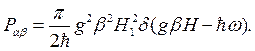 (1.29)
(1.29)
Так как вероятности перехода вверх и вниз одинаковы (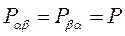 ), то для поглощения необходимо, чтобы населенности двух спиновых состояний были различны. В условиях теплового равновесия это различие обеспечивается за счет больцмановского распределения по уровням с разной энергией (п. 1.5, 1.6). Эффект резонансного поглощения системой электронных спинов называется электронным парамагнитным резонансом (ЭПР). В англоязычной литературе имеет также хождение термин электронный спиновый резонанс. Эффект резонансного поглощения системой ядерных спинов называется ядерным магнитным резонансом (ЯМР).
), то для поглощения необходимо, чтобы населенности двух спиновых состояний были различны. В условиях теплового равновесия это различие обеспечивается за счет больцмановского распределения по уровням с разной энергией (п. 1.5, 1.6). Эффект резонансного поглощения системой электронных спинов называется электронным парамагнитным резонансом (ЭПР). В англоязычной литературе имеет также хождение термин электронный спиновый резонанс. Эффект резонансного поглощения системой ядерных спинов называется ядерным магнитным резонансом (ЯМР).
 2015-07-21
2015-07-21 304
304








