Дифференцирование сложной функции

Пусть функция y=f(x) имеет производную y'=f '(x). Тогда производная от функции y' = f '(x) называется второй производной от функции y = f(x) и обозначается y " = f "(x). Т.е.: y "= f "(x) = [f '(x)]'

Из последней формулы можно вывести метод нахождения производной второго порядка:

1) найти первую производную от исходной функции;

2) продифференцировать полученное выражение второй раз.

Этот способ называется последовательным дифференцированием.

Пример: найти производную второго порядка от функции f(x)=x⁴.

Решение: 1. f'(x)=(x⁴)' =4x³ 2. f''(x)=(f'(x))'=(4x³)'=4=3x²=12x²

Ответ: f ''(x) = 12x²

Производная третьего порядка определяется аналогично - как производная от второй производной, т.е.: f '''(x)=(f ''(x))' =[(f '(x))' ]'

То же последовательное дифференцирование. Например, третья производная от функции из предыдущего примера будет: f '''(x) = (f ''(x))' = (12x²)' = = 12*2x = 24x

Строгое определение производной старшего порядка выглядит так: п роизводной n-ого порядка f ⁽ⁿ⁾ (x) называется производная от производной (n-1)-го порядка:

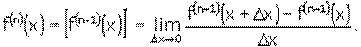
Сложная функция. Пусть у нас дана функция y = f(u). Пусть u является в свою очередь некоторой функцией, например, от переменной x: u = g(x). Т.е. возникает своеобразная "матрешка" - функция от функции: y = f [g (x)]. Такое выражение называется сложной функцией.

Например, если y = u² и u = 1+x³, то у - сложная функция от х, что можно записать следующим образом: y = (1+x³)²

Правило дифференцирования сложной функции дает возможность вычислять ее производную через производные функций, из которых она составлена. Это правило формулируется так: производная сложной функции равна произведению производных от функций, ее составляющих.

Пусть y=f(x), u=g(x). Тогда y'=f'(u)-u'(x)

Пример: пусть дана функция y = (2x²- 1)³. Это сложная функция, составленная из двух простых: кубической функции y = f(u) = u³ и квадратичной u = g(x) = 2x² - 1. Производная исходной функции находится тогда следующим образом: y = f(u) = u³, u = g(x) = 2x² - 1. Значит у '= [(2x²- 1)³] = f '(u) * u'(x) = (u³)' * (2x²- 1)' = 3u² * (2 * 2x - 0) = 3u² * 4x = 12u² x

Однако функция u – промежуточная, введенная для удобства нахождения производной от сложной функции. Поэтому надо вернуться обратно, подставив вместо этой промежуточной функции ее выражение: u=2x²- 1: y'=12u*x=12(2x²-1)=24x³-12x