Достаточные условия существования экстремума

Теорема 1. Если существуют такие а и b, что функция f(х), непре­рывная в точке х₀

(а < х₀ < b), такова, что f(x) > 0 на интервале (а, x₀) и f '(х) < 0 на интервале (х₀, b), то точка x₀ является точкой максимума функции f(х).

Теорема 2. Если функция f (х) непрерывна в точке х ₀, a f ' (x) < 0 на интервале (а, х ₀) и f ′ (x) > 0 на интервале (х ₀, b), то точка х ₀ является точкой минимума функции f (x) .

Таким образом, чтобы найти экстремумы данной функции у = f (х), необходимо:

1. Найти первую производную f ' (х).

2. Приравняв первую производную нулю, отыскать действительные корни х ₁, х ₂ ,... уравнения f ' (х) = 0.

Корни этого уравнения являются критическими точками функции.

3. Для каждой критической точки х_k найти окрестность, не содержа­щую других критических точек, подставить в производную любое число, меньшее х_k из этой окрестности, а затем любое число, большее х_k, из этой окрестности; если при этом знак производной:

а) будет меняться с + на –, то функция при х = х ₁ имеет максимум;

б) будет меняться с – на +, то функция при х = х ₁ имеет минимум;

в) не меняется, то функция при х = х ₁ экстремума не имеет;

4. Найти экстремальные значения функции.

Пример 1. Исследовать функцию 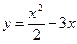, заданную на отрезке [0, 5], на экстремум.

Решение. 1) Находим производную: у' = х – 3.

2) Находим корень производной: х - 3 = 0 <=> х = 3.

3) Находим значение производной в точке х = 2 интервала (0, 3): y' (2) = -1 < 0.

4) Находим значение производной в точке х = 4 интервала (3, 5): y' (4) = 1 > 0.

Производная у' в окрестности точки х = 3 меняет знак с – на +, сле­довательно, в точке

х = 3 находится минимум.

5) находим значение функции в критической точке х = 3: у (3) = 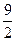- 3∙3 = - 4,5

Таким образом, минимальное значение функции 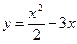равно -4,5.