Исследование функции на выпуклость и точки перегиба

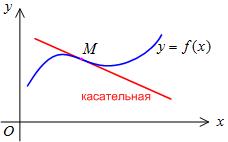
График дифференцируемой функции называется выпуклым вниз на интервале 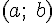, если он расположен выше любой его касательной на этом интервале (рис.13).

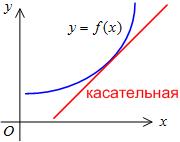
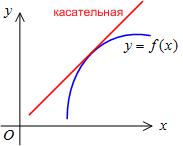
График дифференцируемой функции называется выпуклым вверх на интервале 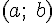, если он расположен ниже любой его касательной на этом интервале (рис.14).

Точка графика непрерывной функции , отделяющая части различной выпуклости, называется точкой перегиба.

Интервалы выпуклости вверх и вниз находятся с помощью следующей теоремы.

Теорема 1. Если функция во всех точках интервала 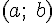имеет отрицательную вторую производную, то есть 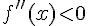, то график функции на этом интервале является выпуклым вверх. Если 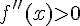во всех точках интервала, то график функции является выпуклым вниз.

Для нахождения точек перегиба функции используется следующая теорема.

Теорема 2. Достаточное условие точки перегиба. Если вторая производная функции при переходе через точку 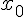, в которой вторая производная равна нулю или не существует, меняет знак, то точка графика с абсциссой 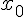является точкой перегиба.

Пример. Исследовать на выпуклость и точки перегиба график функции .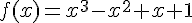

Решение. Находим, что .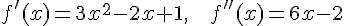

Вторая производная существует на всей числовой оси. Найдем точку, в которой она равна нулю: .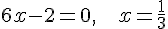

При 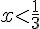получим 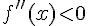, при 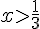имеем 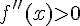, следовательно, на интервале 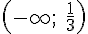график функции является выпуклым вверх,

на интервале 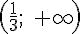график является выпуклым вниз, поэтому точка с абсциссой 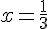является точкой перегиба.

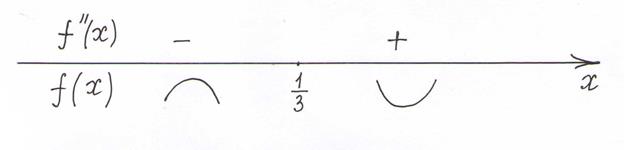
Вопрос. Сколько точек перегиба имеет график функции ?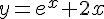

Начало формы

	ни одной