Определение

Определение.

Производной функции 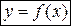в точке 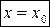называется предел отношения

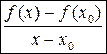при 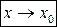, если этот предел существует, и обозначается :

.

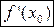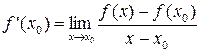Если ввести обозначение 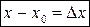(можно назвать эту величину приращением аргумента), то определение запишется в виде:

.

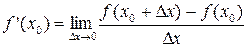Полагая 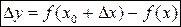(можно назвать эту величину приращением функции), опуская значение аргумента и обозначая производную просто через 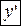, получим еще одну запись:

.

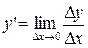Приложения производной.

Пусть функция 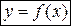имеет в точке 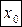производную. Тогда кривая, заданная этой функцией, имеет в точке 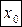касательную и нормаль.

Уравнение касательной:

,

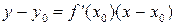где .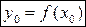

Уравнение нормали:

.

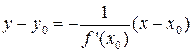2. Односторонние производные функции в точке.

Определение.

Если существует предел 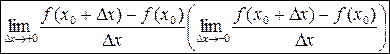, то он называется правой (левой) производной функции 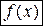в точке 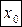и обозначается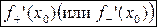

3. Основные правила дифференцирования.

Пусть 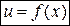и 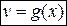имеют производные в точке 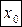. Тогда:

1) их сумма имеет производную в точке :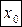

;

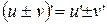2) их произведение имеет производную в точке :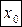

;

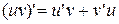3) если в точке 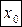, то производную в точке 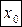имеет частное:

;

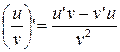4. Производные основных элементарных функций.

1) 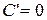( 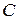- константа);

2) ;

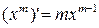3) ;

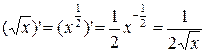4) ;

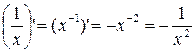5) ;

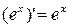6) ;

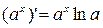7) ;

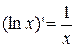8) ;

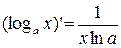9) ;

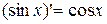10) ;

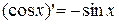11) ;

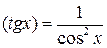12) ;

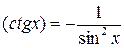13) ;

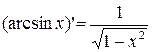14) ;

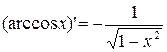15) ;

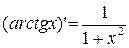16) ;

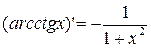17)

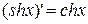
18)

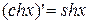
19) 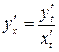(если функция задана параметрически)

5. Дифференциал функции.