Кривина кривої є кількісною мірою відхилення кривої від прямої, а саме: від дотичної прямої.
Скрут – це кількісна міра відхилення кривої від площини, а саме: від стичної площини. Таким чином, скрут вказує наскільки крива відрізняється від форми плоскої кривої.
Положення стичної площини визначається нормальним вектором бінормалі 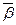 . Швидкість зміни положення
. Швидкість зміни положення 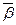 характеризує скрут кривої аналогічно до того, як швидкість зміни вектора дотичної характеризує кривину.
характеризує скрут кривої аналогічно до того, як швидкість зміни вектора дотичної характеризує кривину.
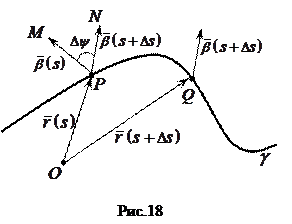 Нехай P – довільна точка кривої
Нехай P – довільна точка кривої 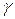 , Q – точка
, Q – точка 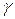 , близька до P. Очевидно, що величина двогранного кута між стичними площинами в точках P і Q дорівнює величині кута між бінормалями в цих точках.
, близька до P. Очевидно, що величина двогранного кута між стичними площинами в точках P і Q дорівнює величині кута між бінормалями в цих точках.
Позначимо:
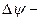 кут між бінормалями в точках P і Q;
кут між бінормалями в точках P і Q;
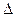 s – довжина дуги PQ кривої
s – довжина дуги PQ кривої 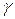 .
.
Абсолютним скрутом 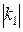 в точці P називається границя відношення кута повороту бінормалі на дузі, що стягується до даної точки, до довжини цієї дуги, тобто в точці P називається границя відношення кута повороту бінормалі на дузі, що стягується до даної точки, до довжини цієї дуги, тобто
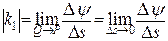 . .
|
Теорема 9. Регулярна крива класу 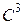 (тричі неперервно диференційовна) в кожній точці з відмінною від нуля кривиною (тричі неперервно диференційовна) в кожній точці з відмінною від нуля кривиною 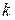 має єдиний абсолютний скрут. Якщо має єдиний абсолютний скрут. Якщо 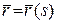 – натуральна параметризація кривої, то абсолютний скрут дорівнює модулю похідної від одиничного вектора бінормалі по s: – натуральна параметризація кривої, то абсолютний скрут дорівнює модулю похідної від одиничного вектора бінормалі по s:
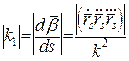 , (18)
де , (18)
де 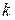 – кривина кривої. – кривина кривої.
|
□ Розглянемо властивості  вектора
вектора 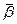 :
:
|
|
|
1) 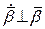 (бо
(бо 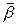 – одиничний вектор, отже
– одиничний вектор, отже 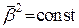 ,
, 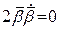 );
);
2) 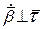 (оскільки
(оскільки 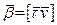 , з першої формули Френе (13):
, з першої формули Френе (13): 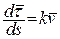 і
і
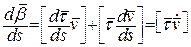 ); (19)
); (19)
3) отже 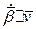 , тому
, тому 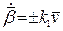 . Візьмемо в цій рівності знак мінус:
. Візьмемо в цій рівності знак мінус: 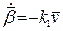 .
.
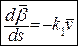 (третя формула Френе). (20)
(третя формула Френе). (20)
Таким чином 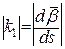 .
.
Знайдемо тепер 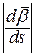 .
. 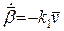 ,
, 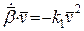 або
або 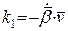 .
.
Враховуючи (19), (13) і розглядаючи кривину k як функцію s, маємо:
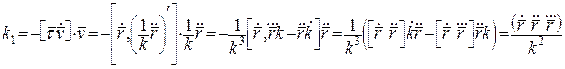 .
.
Отже, 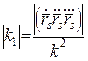 .■
.■
4.6. Скрут кривої в довільній параметризації
Нехай 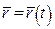 . Будемо вважати, що
. Будемо вважати, що 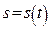 і
і 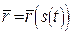 . Як і в знаходженні кривини, похідні вектор-функції по натуральному параметру s будемо позначати з крапкою (
. Як і в знаходженні кривини, похідні вектор-функції по натуральному параметру s будемо позначати з крапкою (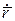 ,
, 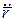 і т.д.), а похідні по довільному параметру t зі штрихом (
і т.д.), а похідні по довільному параметру t зі штрихом (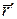 ,
, 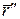 і т.д.).
і т.д.).
Для натуральної параметризації маємо: 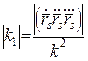 .
.
Виразимо похідні 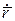 ,
, 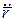 ,
, 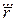 по s через похідні
по s через похідні 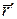 ,
, 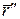 ,
, 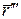 по параметру t.
по параметру t.
Раніше було показано, що 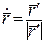 ;
; 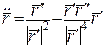 .
.
Для знаходження 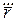 використаємо отриману вище в пункті 4.3 формулу:
використаємо отриману вище в пункті 4.3 формулу: 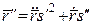 . Тоді
. Тоді 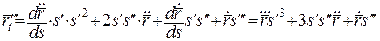 , звідки
, звідки 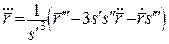 .
.
Нагадаємо, що для довільної параметризації 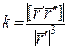 ,
, 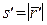 ,
, 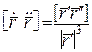 , тому
, тому 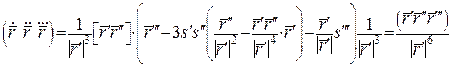 .
.
Таким чином, 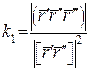 – абсолютний скрут в довільній параметризації.
– абсолютний скрут в довільній параметризації.
Скрутом кривої називається величина 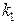 , яка обчислюється за формулою:
, яка обчислюється за формулою: 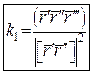 . (21)
. (21)
В скалярній формі: 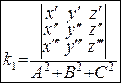 (21')
(21')
Зауваження. Плоскі криві – це криві нульового скруту.
Задача. Знайти скрут гвинтової лінії 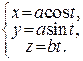
Розв’язання.
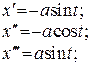
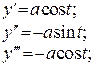
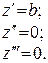
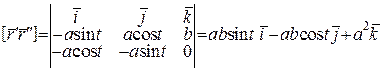 .
.
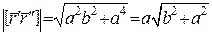 .
.
Мішаний добуток 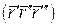 обчислимо як скалярний добуток
обчислимо як скалярний добуток 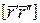 і
і 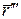 :
:
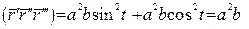 .
.
Тоді 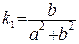 .
.
Таким чином, скрут гвинтової лінії є сталою величиною. Якщо 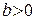 – «правогвинтова нарізка»; якщо
– «правогвинтова нарізка»; якщо 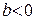 – «лівогвинтова».
– «лівогвинтова».
Відповідь: 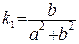 .
.
 2015-07-14
2015-07-14 1066
1066








