Складання і віднімання замість множення

До винаходу таблиць логарифмів для полегшення множення багатозначних чисел застосовувалися так звані простаферичні таблиці (від грецьких слів «прос тезис» - додавання і «афайрезис» - віднімання), що являють собою таблиці значень функції 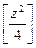при натуральних значеннях z. Оскільки при a і b цілих 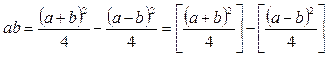(числа a+b і a-b або обидва парні, або обидва непарні; в останньому випадку дробові частини у 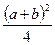і 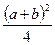однакові), то множення a на b зводиться до визначення a+b і a-b і, накінець, різниці чисел 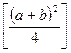і 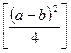, узятих з таблиці.

Для перемноження трьох чисел можна скористатися тотожністю:

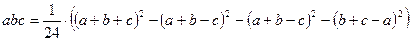
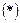з якої виходить, що за наявності в таблиці значень функції 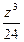обчислення добутку abc можна звести до визначення чисел: a+b+c, a+b-c, a+c-b, b+c- a і по ним – за допомогою таблиці – правої частини рівності (*).

Проведемо як приклад таку таблицю для 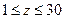. У таблиці дані: великими цифрами – значення 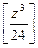, а дрібними – значення k, де при .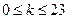

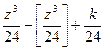		Одиниці
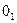
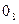
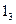
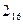
Десятки							55	90	147	218	309
	4116	5511	720	9113	1148	14015	17016	20417	2430	28519
	3338	38521	44316	50623	5760	6511	7328	8203	91416	10165

Неважко, користуючись формулою (*) і таблицею, отримати:

9×9×9=820₃-30₉-30₉=729,

17×8×4=1016₅-385₂₁-91₁₃+5₅=544(перевірте!).

Функція [x] (ціла частина x)

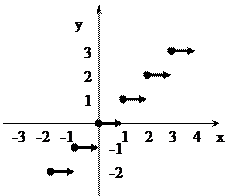Функція [x] дорівнює найбільшому цілому числу, не перевищуючому x (x – будь-яке дійсне число). Наприклад:

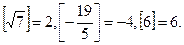
Функція [x] має «точки розриву»: при цілих значеннях x вона «змінюється стрибком».

На рис.2 даний графік цієї функції, причому лівий кінець кожного з горизонтальних відрізань належить графіку (жирні), а правий – не належить.

Спробуйте довести що якщо канонічне розкладання числа n! є 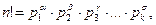то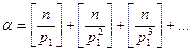

Аналогічні формули мають місце для β, γ, …, σ.

знаючи це, легко визначити, наприклад, скількома нулями закінчується число 100! дійсно, нехай 100!=2^α·3^β·5^γ·…·97^σ·. Тод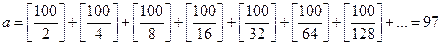і, і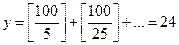

Отже, 100! ділиться на (2·5)²⁴, тобто закінчується двадцятьма чотирма нулями.