2015-08-12
512
Дальнейшее изложение будем вести для функций двух переменных, как более наглядное, хотя результаты естественным образом обобщаются на случай трех и более переменных.
Число А называется пределом функци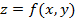и 
при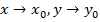 
, если для любого 
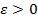, найдется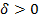 
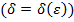, такое, что для всех точек 
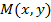, отстоящих от точки 
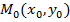на расстояние, меньшее d, 
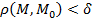, выполняется неравенство: 
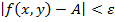. Обозначается: 
.
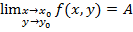Пример: 6) Найти предел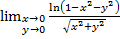 
, 7) Доказать, что 
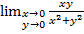не существует.
Решение: 6) Обозначим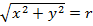 
, тогда условие 
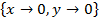Û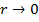 
.
Предел запишется в виде: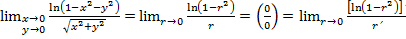 
=
= 
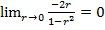. Здесь применили правило Лопиталя.
7) Будем приближаться к точке (0,0) по прямым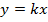 
(k – const.). Тогда:
.
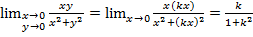Как видим, значение предела зависит от углового коэффициента прямой k. Например, при значениях k = 1 и k = 2 предел будет разный (соответственно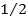 
и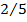 
). Что и доказывает, что предел не существует.
Функция 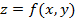непрерывна в точке 
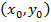, если она: 1) определена в точке 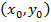; 2) имеет конечный предел при 
, 
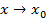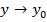; 3) этот предел равен значению функции в точке 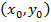, то есть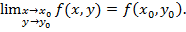 
Говорят, что функция 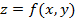непрерывна в некоторой области D, если она непрерывна в каждой точке этой области.
