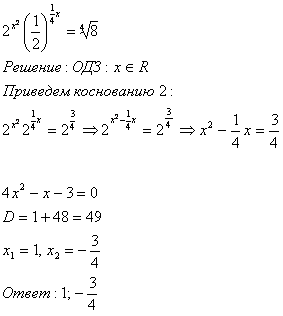
33 Потенцирование (от нем. potenzieren, возведение в степень) — это нахождение числа по известному значению его логарифма, то есть решение уравнения:
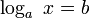
Из определения логарифма вытекает, что x = ab. Таким образом, потенцирование означает возведение основания логарифма в степень, равную значению логарифма. Например, если десятичный логарифм числа равен L, то искомое число равно 10 L.
35
Показательные неравенства
При решении показательныx неравенств используются следующие утверждения:
A.1. Если a > 1, неравенство
a f (x) > a g (x)
равносильно неравенству
f (x) > g (x).
Аналогично, a f (x) < a g (x) Û f (x) < g (x).
A.2. Если 0 < a < 1, неравенство
a f (x) > a g (x)
равносильно неравенству
f (x) < g (x).
Аналогично, a f (x) < a g (x) Û f (x) > g (x).
A.3. Неравенство
| [ h (x)] f (x) > [ h (x)] g (x) | (1) |
равносильно совокупности систем неравенств
| 
| h (x) > 1, |
| f (x) > g (x), | ||
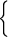
| 0 < h (x) < 1, | |
| f (x) < g (x). |
Замечание.. Если знак неравенства (1) нестрогий, дополнительно рассматривается и случай
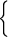
| h (x) = 1, |
| x Î D (f)Ç D (g), |
где D (f) (D (g)) означает область определения функции f (g).
A.4. Если b ≥ 0, неравенство
af (x) < b
не имеет решений (следует из свойств показательной функции).
A.5. Если b ≤ 0, множеством решений неравенства af (x) > b является x Î D (f).
A.6. Если a > 1, b > 0, неравенство
af (x) > b
равносильно неравенству
f (x) > log ab.
Аналогично, a f (x) < b Û f (x) < log ab.
A.7. Если 0 < a < 1, b > 0, неравенство
a f (x) > b
равносильно неравенству
f (x) < log ab.
Аналогично, a f (x) < b Û f (x) > log ab.
36 Логарифмическое уравнение – это трансцендентное уравнение, в котором неизвестное входит в аргумент логарифма.
При решении логарифмических уравнений используются два основных метода: 1) переход от уравнения 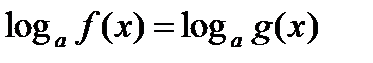 к уравнению вида
к уравнению вида 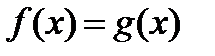 ; 2) введение новых переменных.
; 2) введение новых переменных.
Замечание. Так как область определения логарифмической функции только множество положительных действительных чисел, при решении логарифмических уравнений необходимо либо находить область допустимых значений уравнения (ОДЗ), либо после нахождения решений уравнения делать проверку.
Рассмотрим некоторые виды простейших логарифмических уравнений.
Решение простейшего логарифмического уравнения 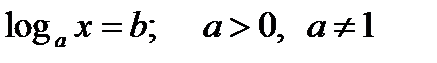
37. Логарифмические неравенства
Любое логарифмическое неравенство может быть в конечном счете сведено к неравенству вида 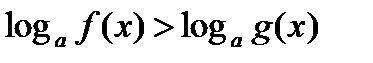 ……………………………………..(1)
……………………………………..(1)
Решение такого неравенства основывается на следующих теоремах:
1. Если а > 1, то неравенство вида (1) равносильно системе неравенств: 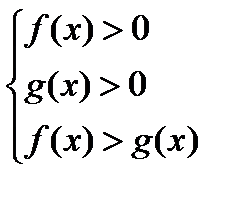
2. Если 0 < а < 1, то неравенство (1) равносильно системе неравенств: 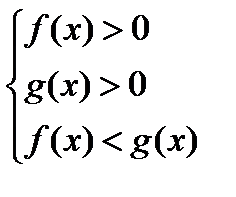
Замечания 1. Первые два неравенства систем задают область допустимых решений неравенства (1).
2. В системе из теоремы 1 можно опустить первое неравенство, так как оно следует из второго и третьего. Аналогично в системе из теоремы 2 можно опустить второе неравенство.
38 Показательная функция — математическая функция 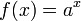 , где a называется «основанием», а x — «показателем» степени.
, где a называется «основанием», а x — «показателем» степени.
§ 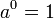
§ 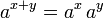
§ 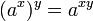
§ 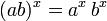
Используя функцию натурального логарифма 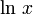 , можно выразить показательную функцию с произвольным положительным основанием через экспоненту:
, можно выразить показательную функцию с произвольным положительным основанием через экспоненту:
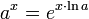
Эта связь позволяет ограничиться изучением свойств экспоненты.
Аналитические свойства:
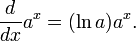
В частности:
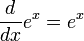
 2015-08-12
2015-08-12 429
429








