Энергетический принцип

Уравнение (2.1.31) можно записать следующим образом:

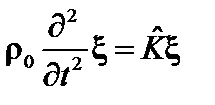. (2.2.1)

Здесь 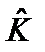– дифференциальный оператор. Можно показать, что если оператор 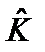– самосопряженный, то есть 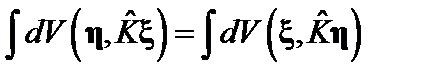, то можно написать функционал 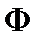, вариация которого дает исходное уравнение.

В Фурье-представлении двукратное дифференцирование по времени заменяется на умножение на квадрат частоты 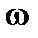. Если мнимая часть частоты оказывается больше нуля, то система неустойчива. Анализ устойчивости может быть существенно упрощён. Для такого уравнения можно построить вариационный принцип. Подставляя в этот принцип вместо точного решения уравнения приближенную пробную функцию, качественно описывающую характер решения, можно с хорошей точностью получить собственные значения 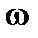, то есть исследовать устойчивость системы.

Домножим уравнение (2.2.1) на 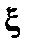скалярно и проинтегрируем по объёму и по времени по частям от 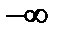до t и по пространству, полагая .

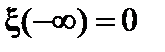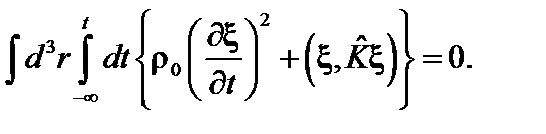(2.2.2)

Это равенство справедливо при произвольном t. Поэтому можно считать, что

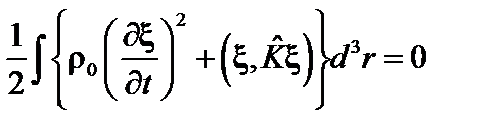. (2.2.3)

Первый член в этом выражении можно интерпретировать как кинетическую энергию системы 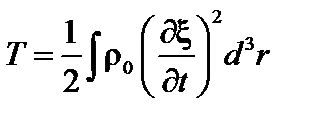, а второй, 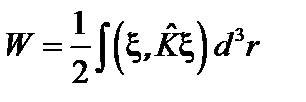, – как потенциальную.

Если 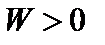при всех возможных смещениях от положения равновесия, то система устойчива. В случае уравнения (2.1.31) потенциальная энергия имеет вид

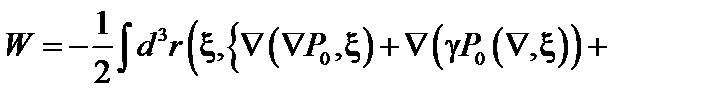
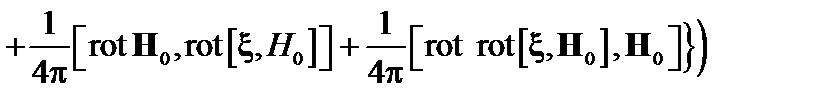. (2.2.4)

Преобразуем первый интеграл в фигурных скобках. Интегрирование ведется по объёму, занятому плазмой, так как вне его давление равно нулю. Обозначим

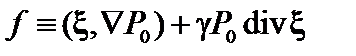. (2.2.5)

Интегрируя по частям, находим

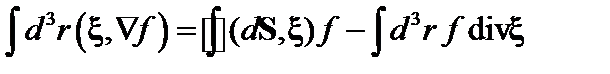. (2.2.6)

В первом члене интегрирование ведётся по поверхности, ограничивающей плазму. Рассмотрим теперь последний член в интеграле (2.2.4). Обозначим

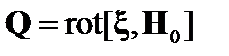. (2.2.7)

Последний член в (2.2.4) преобразуется как

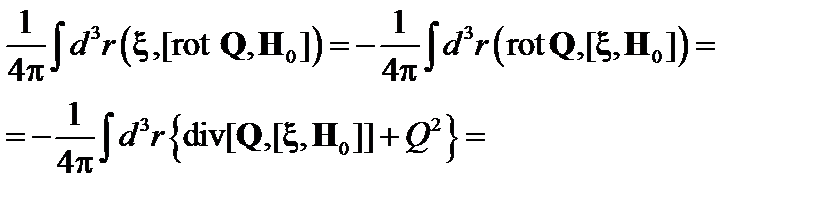
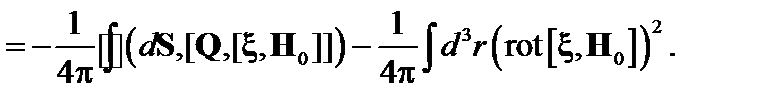(2.2.8)

В первом интеграле интегрирование снова ведется по границе плазмы. Раскрывая двойное векторное произведение и учитывая, что поверхность плазмы параллельна магнитному полю, получаем выражение для потенциальной энергии

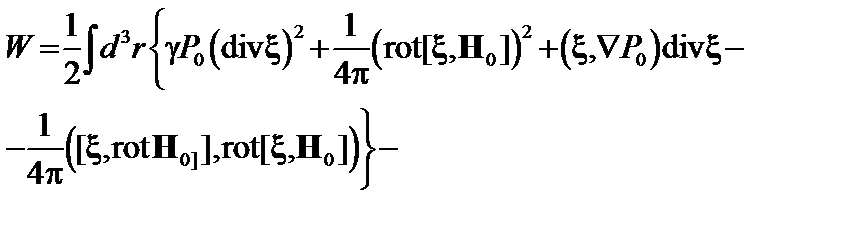
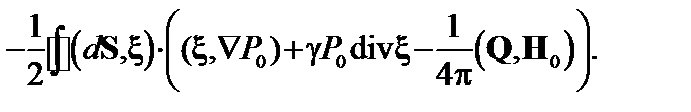(2.2.9)

Поверхностный интеграл

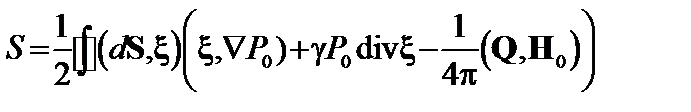
преобразуем с помощью равенства (3.1.38):

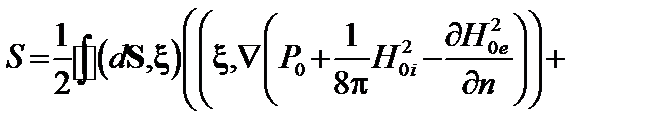
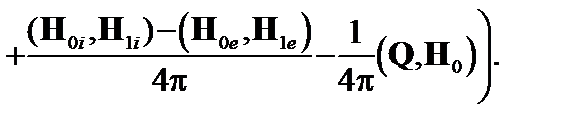(2.2.10)

Величину надо вычислять на подходе к границе плазмы со стороны плазмы. Эту величину можно определить, подставляя уравнение (2.1.13) в (2.1.16) и интегрируя последнее по времени:

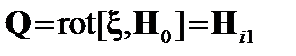. (2.2.11)

Скалярное произведение 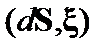можно выразить через модуль элемента поверхности и нормальную к поверхности составляющую смещения, 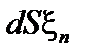. Тогда

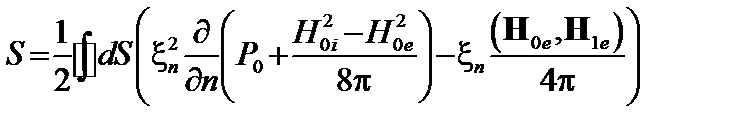. (2.2.12)

Последний член можно преобразовать так:

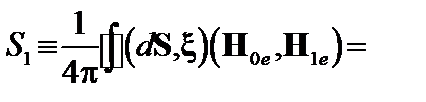
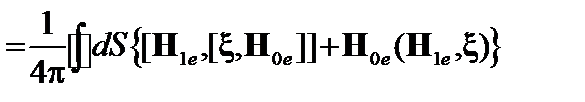. (2.2.13)

Последний член обращается в ноль, так как магнитное поле на границе плазмы перпендикулярно поверхности плазмы. Снова перейдем к интегрированию по объёму, но теперь будем вести интегрирование по вакуумной области. При этом знак нормали к поверхности плазмы имеет другой знак

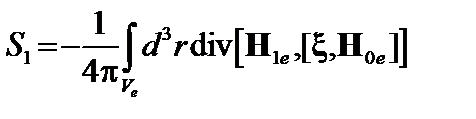. (2.2.14)

Учитывая, что в вакууме 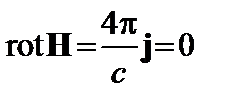, раскроем двойное векторное произведение и подставим 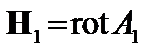. При этом получаем

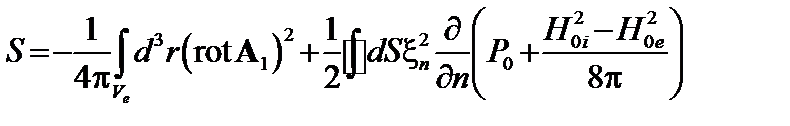. (2.2.15)

И окончательно

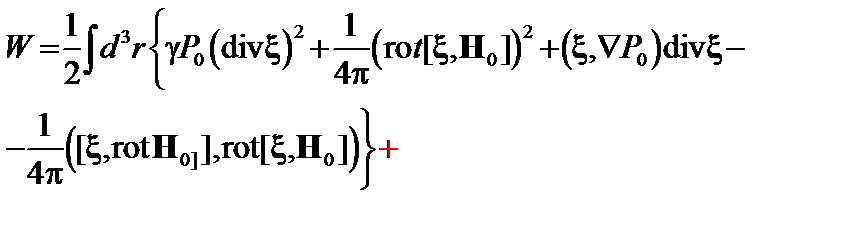
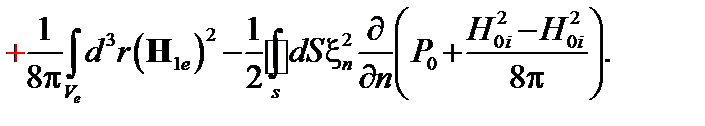(2.2.16)

Пользоваться энергетическим признаком удобно в тех случаях, когда нужно получить общие сведения об устойчивости плазменной конфигурации. Он, в частности, позволяет приближенно быстро найти область неустойчивости, что при нахождении её методом малых колебаний требует значительного времени.