Неустойчивость на запертых частицах

До сих пор мы изучали неустойчивости, которые с той или иной степенью точности можно исследовать в пределе цилиндра с отождествленными концами. Однако только в торе развивается целый ряд неустойчивостей, которые играют большую роль в аномальных переносах тепла и частиц. Таковы, например, баллонные моды (см., например, [4]). Рассмотрим одну из таких неустойчивостей – бесстолкновительную неустойчивость на запертых частицах.

В токамаке запертые частицы совершают периодические движения между точками отражения аналогично частицам в пробкотроне. Поэтому можно ожидать развития аналогичной неустойчивости. Но запертые частицы в токамаке погружены в море пролётных частиц, которые частично компенсируют разделение зарядов, создаваемое запертыми. Поэтому условие устойчивости будет несколько иным.

Очевидно, что для решения задачи должно быть использовано кинетическое уравнение. В нулевом приближении оно имеет вид

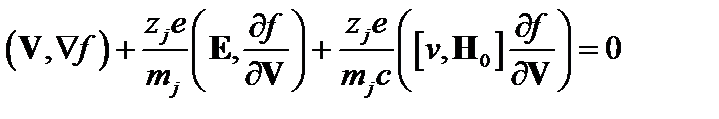. (3.7.1)

Для простоты положим 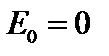. Более того, если возмущение сильно локализовано по радиусу, можно перейти в систему отсчёта, в которой 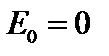. Пусть функция распределения 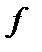мало отличается от максвелловской с локальным значением температуры. Тогда можно написать

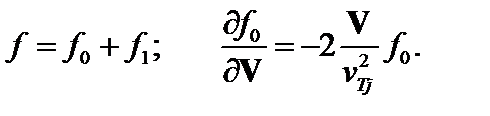(3.7.2)

С учётом того, что 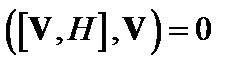, уравнение (3.7.1) примет вид:

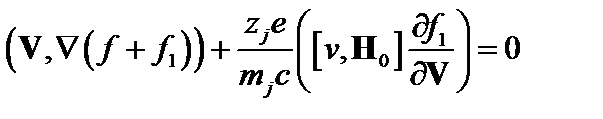. (3.7.3)

Будем рассматривать неустойчивость в пределе сильного магнитного поля, 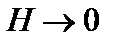, когда можно пренебречь членом 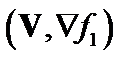. Тогда уравнение (3.7.3) перепишем так:

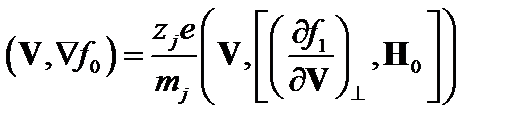. (3.7.4)

Это равенство справедливо при любых (нерелятивистских) скоростях, поэтому справедливо равенство

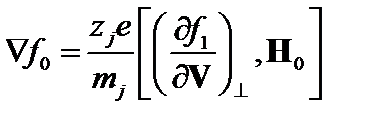. (3.7.5)

В дальнейшем для краткости будем опускать индекс j, означающий сорт частицы. Выразим производную 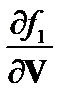из этого уравнения и проинтегрируем по скоростям. В результате получаем поправку к 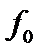, связанную с тороидальностью:

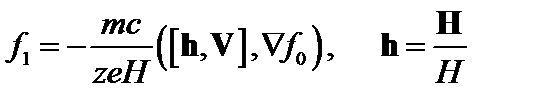. (3.7.6)

Теперь вычислим поправку к функции распределения, связанную с возмущением электрического поля. Соответствующее кинетическое уравнение в линейном приближении имеет вид

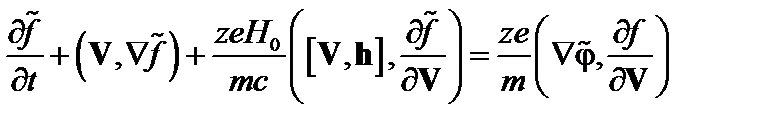. (3.7.7)

Здесь тильдой обозначена поправка к функции распределения, связанная с возмущением электрического поля 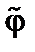. Мы считаем возмущения чисто потенциальными, 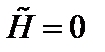. Левая часть этого уравнения – это полная производная по времени

,

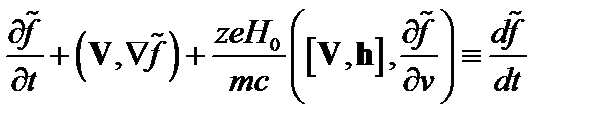то есть можно написать

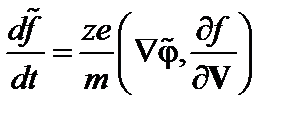(3.7.8)

и проинтегрировать полученное уравнение по времени от 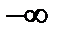до

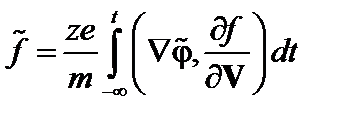. (3.7.9)

Возмущение плотности находим, интегрируя 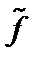по скоростям. Теперь для получения дисперсионного уравнения достаточно приравнять возмущения плотностей электронов и ионов. Учтём, что

.

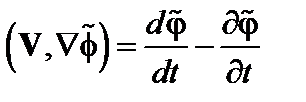Кроме того,

.

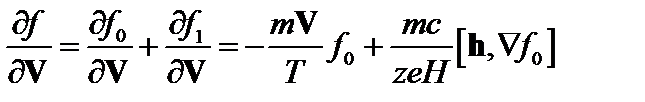Возмущенный потенциал периодичен по азимутальному и тороидальному углам. Поэтому будем искать его в виде 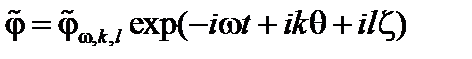. Здесь 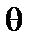и 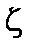– азимутальный и тороидальный углы, 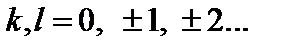Индексы 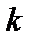и мы для краткости будем опускать.

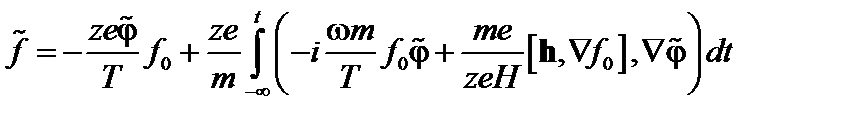. (3.7.10)

Прямой фурье-анализ здесь затруднён, так как магнитное поле само зависит от полоидального угла.

Положим 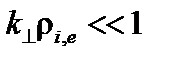и пренебрежём отклонением частиц от ведущего центра. Тогда в системе координат, в которой силовые линии прямые, получим возмущенную плотность.

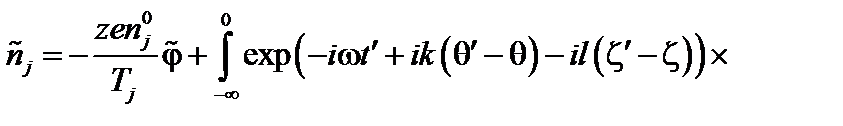
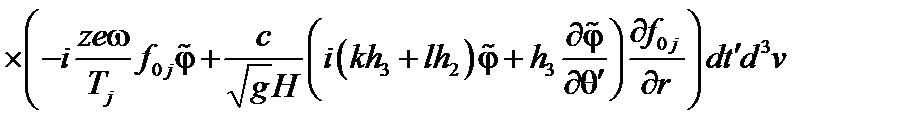. (3.7.11)

Здесь 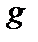– определитель метрического тензора 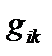(см. раздел 3.2), 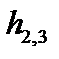– ковариантные компоненты вектора 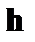. В случае малой тороидальности уравнение (3.7.11) упрощается. Кроме того, полагая 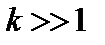, членом, пропорциональным 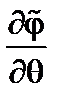, можно пренебречь по сравнению с членом, пропорциональным 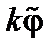. В результате, приравнивая 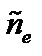и 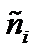, получаем

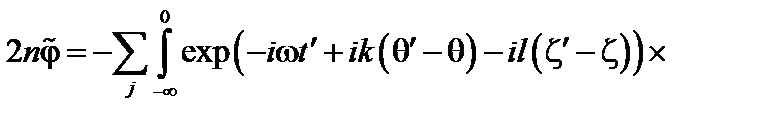
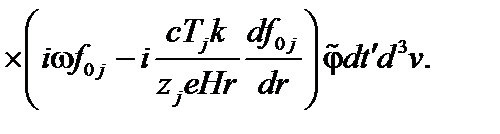(3.7.12)

Здесь мы положили 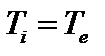. При интегрировании по скоростям нужно отдельно проинтегрировать пролётные и запертые частицы. Для пролётных частиц

; ;

.

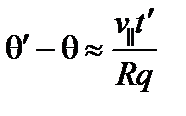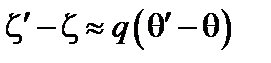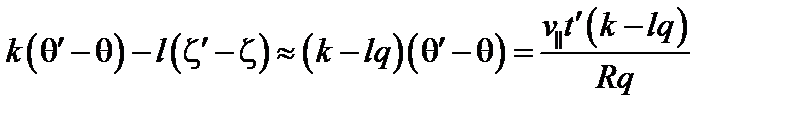Отклонением пролётных частиц от магнитной поверхности можно пренебречь. Интегрирование по времени дает множитель

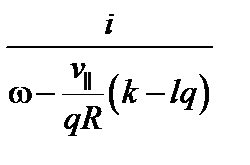. (3.7.13)

Частота оценивается как ионная дрейфовая частота, 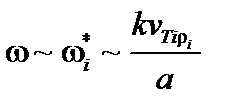, где 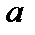– характерный масштаб плотности или давления. Эта частота существенно меньше обратного времени пролёта электрона вдоль одного оборота силовой линии по тороидальному углу, 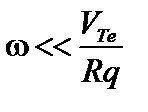, даже если 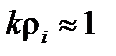. Для ионов 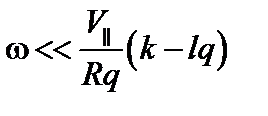. Действительно,

,

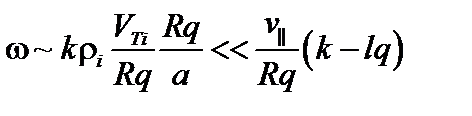если 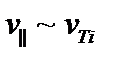и выполняется обычное условие 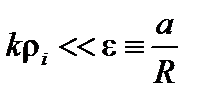, а также мода не слишком близка к резонансу, 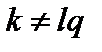. В этом случае множитель (3.7.13) мал и вкладом от пролётных частиц можно пренебречь.

Для запертых частиц можно написать ([8])

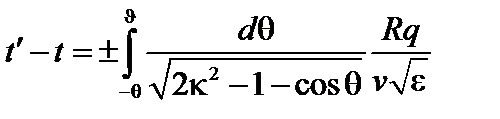; (3.7.14)

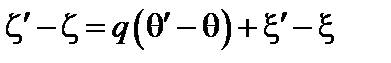. (3.7.15)

Характер траектории можно хорошо видеть на примере глубоко запертых частиц:

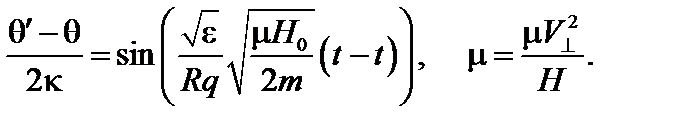(3.7.16)

Частицы совершают периодические колебания по углу 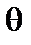. По углу 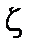наряду с колебаниями они совершают также поступательное движение со скоростью 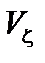, 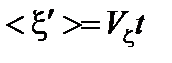. Таким образом, интегрирование по 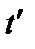можно свести к интегрированию по периоду колебаний, соответствующему колебаниям между точками отражения и суммированию по этим отрезкам времени. Тогда мы получим интегральное уравнение

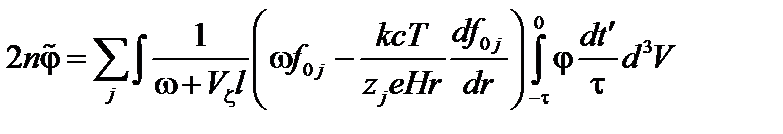, (3.7.17)

переходя к интегрированию по 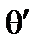от интегрирования по 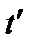. В результате находим интегральное уравнение для 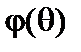. Решая его, получаем собственные функции и собственные значения для частоты. Условие устойчивости, при котором 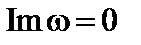, имеет вид

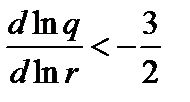, (3.7.18)

что соответствует падению 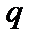с радиусом. Обычно в токамаке величина 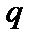растёт с радиусом. Таким образом, неустойчивость на запертых частицах должна развиваться и приводить к аномальным переносам практически при любом профиле тока. Более подробно эта неустойчивость описана в работе [5].