Тиринг-мода

Рассмотренные в предыдущей главе неустойчивости идеальной плазмы развиваются, как правило, за очень малые времена порядка отношения размера плазмы к альфвенвской скорости. В плазме могут развиваться и другие неустойчивости, связанные с конечной её проводимостью. Характерные времена их развития существенно больше, однако и они играют важную роль. За такие времена нарушается вмороженность силовых линий в плазму. В частности, может происходить перезамыкание силовых линий и меняться топология магнитного поля. Пример такого перезамыкания приведен на рис. 11.

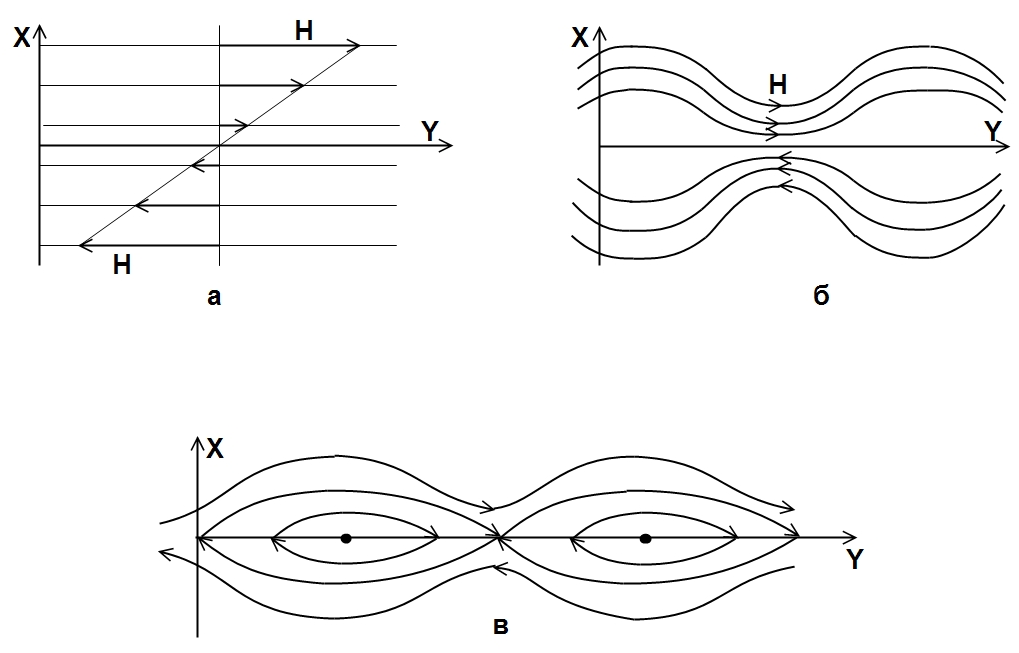
Рис. 11. Перезамыкание силовых линий

Пусть в плоском слое плазмы течёт ток в направлении оси z. Силовые линии в начальный момент времени параллельны оси 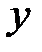(рис. 11, а). Такая конфигурация может быть неустойчивой. Как известно, параллельные токи притягиваются, поэтому однородный вначале ток начинает расслаиваться на отдельные волокна. Силовые линии начинают изгибаться (рис. 11, б). Токи, текущие вблизи поверхности 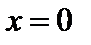, при конечной проводимости гасят друг друга (в случае бесконечной проводимости они лишь сгущались бы вблизи этой поверхности), и магнитные поверхности меняют топологию, образуя «островную» структуру (рис. 11, в).

Опишем эту картину математически. Пусть 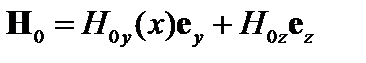. Закон Ома в простейшей форме имеет вид

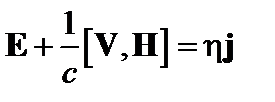. (4.1.1)

Для простоты будем считать, что удельное сопротивление постоянно: 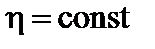. Взяв 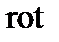от этого уравнения и принимая во внимание, что 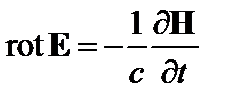, получаем

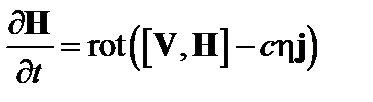. (4.1.2)

Преобразуем первый член в правой части уравнения с учётом того, что :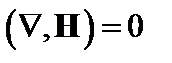

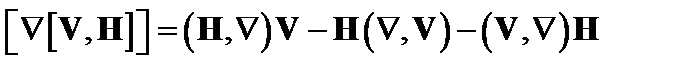. (4.1.3)

Тогда уравнение (4.1.2) можно переписать в виде уравнения диффузии с некоторыми дополнительными членами:

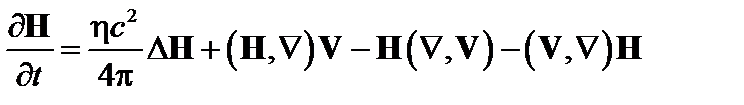. (4.1.4)

Здесь мы учли, что .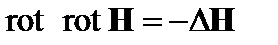

К этому уравнению необходимо добавить уравнение, описывающее движение плазмы. В одножидкостном приближении, пренебрегая вязкостью, имеем

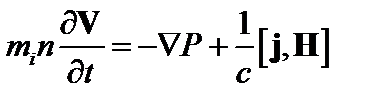. (4.1.5)

Членом 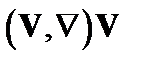мы пренебрегли, так как он квадратичен по V и в линейное приближение вклада не даст. Последний член в правой части преобразуем с помощью следующих операций:

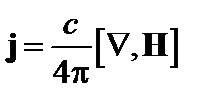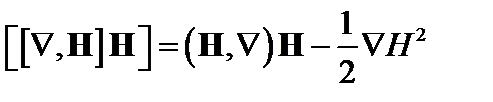; . (4.1.6)

Множитель ½ перед последним членом в правой части связан с тем, что оператор «набла» действует лишь на одно Н в левой. Представим Н как сумму невозмущённого поля и малого возмущения, подставим (4.1.6) в (4.1.5). В нулевом приближении получим

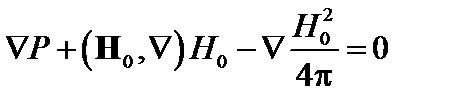. (4.1.7)

В линейном приближении

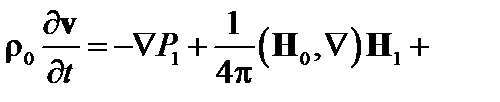
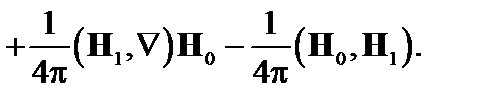(4.1.8)

Возьмем 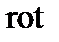от этого уравнения.

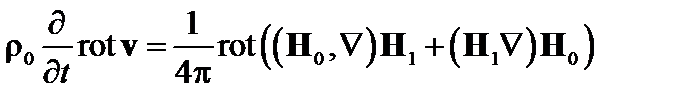. (4.1.9)

H ₀ зависит только от х, поэтому 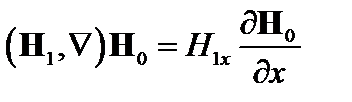. Введем функцию

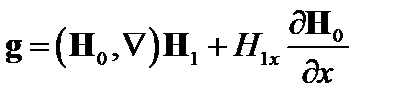(4.1.10)

и подействуем оператором 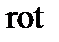на уравнение (4.1.9):

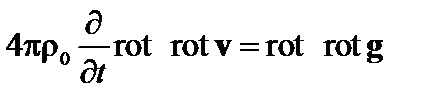. (4.1.11)

Правую часть и левую части этого уравнения с точностью до постоянного множителя можно представить в виде

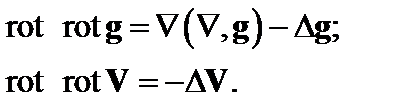(4.1.12)

Здесь мы предположили, что плазма несжимаема, 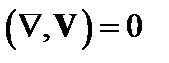. Все коэффициенты перед H и v в уравнении (4.1.11) только от х, и уравнение можно разложить в интеграл Фурье по у, z и t, 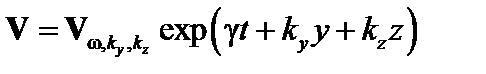. В дальнейшем индексы у фурье-компонент будем опускать. Итак, в фурье-представлении уравнение (4.1.9) имеет вид

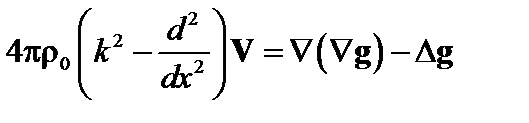. (4.1.13)

Здесь 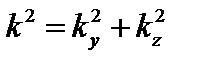. С учётом 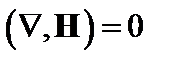находим

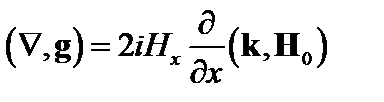. (4.1.14)

Вычислим теперь x -составляющую вектора :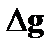

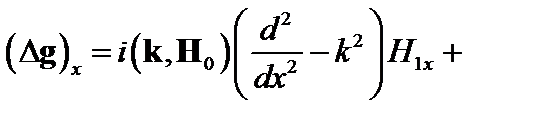
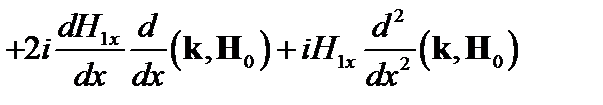. (4.1.15)

Подставим теперь выражения (4.1.14) и (4.1.15) в x -компоненту уравнения (4.1.13). Окончательно получаем следующее уравнение:

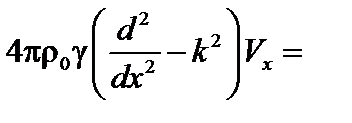
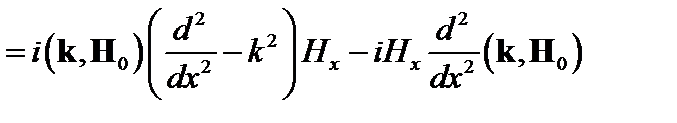. (4.1.16)

Второе уравнение окончательной системы – это фурье-компо-нента уравнения (4.1.4).

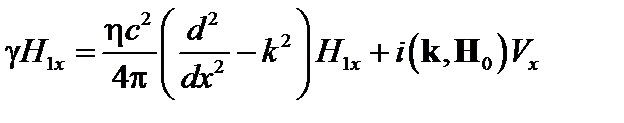. (4.1.17)

Как видно, в полученную систему уравнений входят только х -компоненты скорости и магнитного поля.

Для начала рассмотрим случай идеальной плазмы, то есть устремим удельное сопротивление 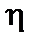к нулю. Тогда

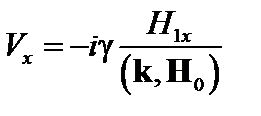. (4.1.18)

При 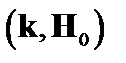, стремящемся к нулю, скорость обращается в бесконечность, то есть теория неприменима, и мы должны учитывать конечное сопротивление. Пусть поверхность 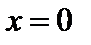совпадает с поверхностью 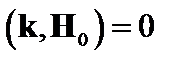. Тогда вблизи этой поверхности можно написать 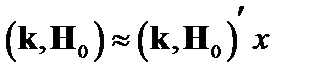, где штрих означает производную по 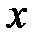. Вдали от этой поверхности при большой проводимости можно пользоваться идеальной гидродинамикой и формулой (4.1.18). В этом случае (4.1.16) можно переписать так:

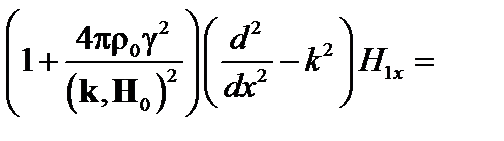
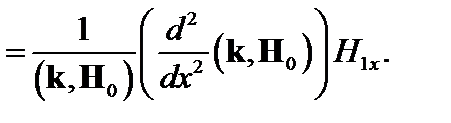(4.1.19)

Вблизи порога неустойчивости 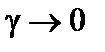, и уравнение (4.1.19) упрощается:

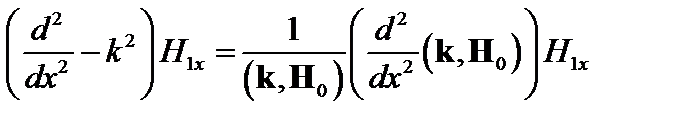. (4.1.20)

Решим модельную задачу, представив 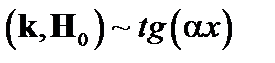. В выбранной нами системе координат 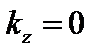. Решение этой задачи известно:

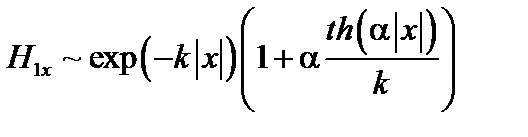. (4.1.21)

Однако это решение терпит разрыв производной в точке 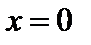. Действительно, при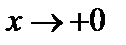

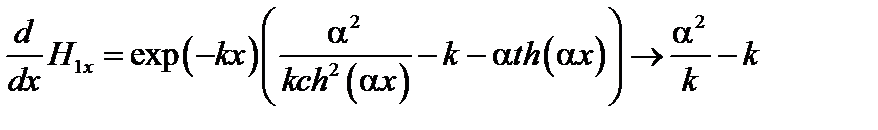при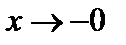

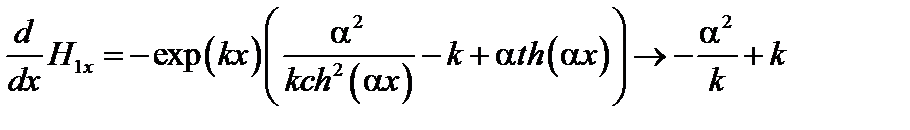Следовательно, приближение идеальной МГД здесь неприменимо и надо вводить конечную проводимость. Будем называть эту область резистивной. Пусть ширина этой области 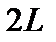много меньше длины волны, 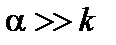. Тогда в уравнении (4.1.16) можно пренебречь величиной 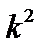в круглых скобках, и это уравнение перепишется так:

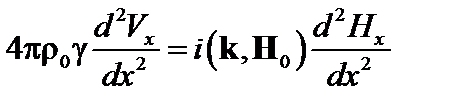. (4.1.22)

К этому уравнению добавляется уравнение (4.1.17) при :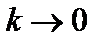

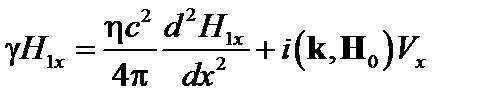. (4.1.23)

Как уже указывалось, в этой узкой области величина 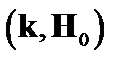практически линейно зависит от 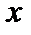, , 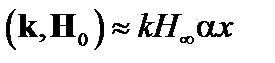где 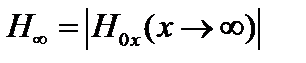, и последним членом в (4.1.16) мы пренебрегли.

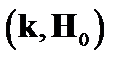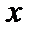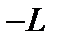Разделим уравнение (4.1.23) на и проинтегрируем его по от до :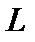

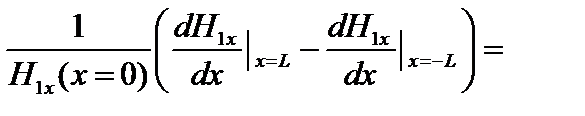
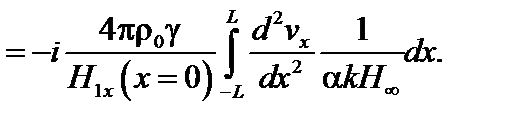(4.1.24)

Введём величину

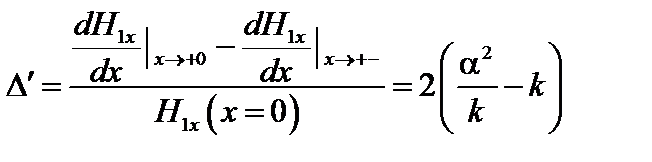. (4.1.25)

Тогда уравнение (4.1.24) перепишется так:

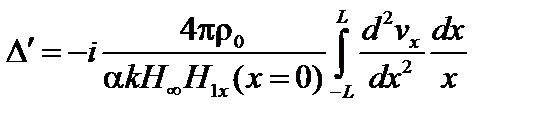. (4.1.26)

Подставим 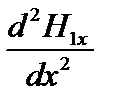из уравнения (4.1.22) в уравнение (4.1.23).

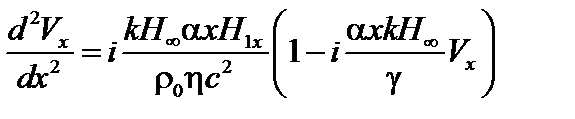. (4.1.27)

Инкремент неустойчивости можно вычислить, подставляя это выражение в правую часть уравнения (4.1.26), а 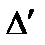– из (4.1.25) и пользуясь «приближением постоянного H», то есть, считая, что в правой части (4.1.27) .

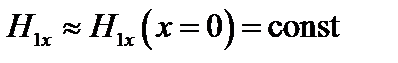Качественно инкремент неустойчивости можно оценить так. В резистивной зоне

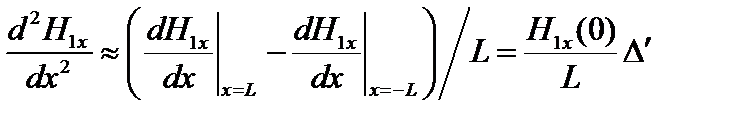. (4.1.28)

Тогда, считая в уравнении (4.1.23) оба члена в правой части одного порядка, для оценки можно написать

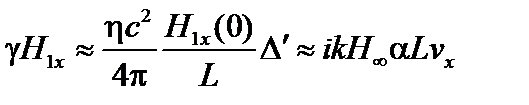(4.1.29)

или по порядку величины

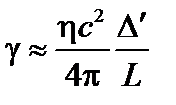. (4.1.30)

Таким образом, условие устойчивости сводится к следующему:

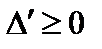Для тог чтобы найти 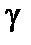, надо оценить 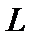. По порядку величины 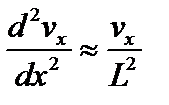. Подставляя эту оценку и выражение (4.1.28) в выражение (4.1.22), находим

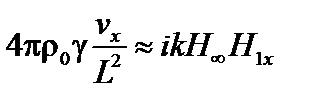. (4.1.31)

Используя (4.1.29) и (4.1.30), сокращаем на 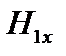и получаем

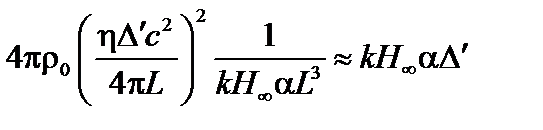. (4.1.32)

В результате находим толщину резистивного слоя:

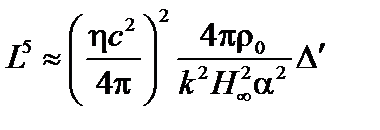. (4.1.33)

Введём два времени: альфвеновское

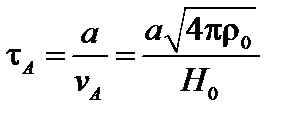(4.1.34)

и резистивное

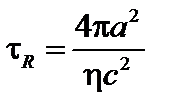, (4.1.35)

а также магнитное число Рейнольдса

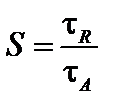(4.1.36)

и выразим через него L:

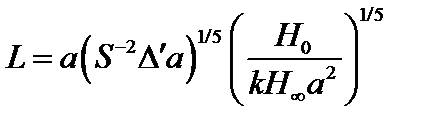. (4.1.37)

Окончательно

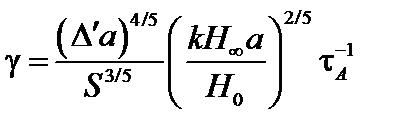. (4.1.38)

Напомним, что 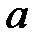– поперечный размер плазменного слоя. Как видно из полученного результата, инкремент тиринг-моды (резистивной неустойчивости) существенно меньше обратного альфвеновского времени, характерного для развития идеальных мод.