Условие устойчивости линейной дискретной системы. Критерий Рауса-Гурвица

Если система была выведена из устойчивого состояния под некоторыми воздействиями, и если она затем вернется в исходное состояние, то система устойчива, если не вернется, то не устойчива.

Мат. Модель д.у. 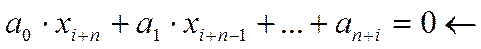разностное уравнение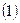

Поведение системы, выраженное разност уравнением.

Решение складывается из общего решения однородного уравнения. Общее решение описывает собственные колебания: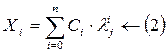

C*i-произвольные коэффициенты.

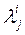-это норм. характеристич. разность уравнения.

Характеристическое уравнение это: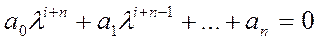

Если мы найдем норм X и Y(конкретные значения, зависящие от параметров, 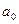) и подставив в уравнение найдем то найдем конкретные норм и конкретные значения дают конкретный процесс.

2-опис собствен колебаний.

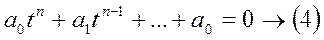
Корни x и y собст. колебания. Это выражение справедливо, когда корни простые.

Система устойчива если корни по модулю меньше единицы.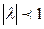

Для устойчивой системы корни находятся в окружности единичного радиуса.

Собственные колебания б/затухать - достаточно устойчивы. Как в непрерывных системах.

Критерий устойчивости позволяет следить за устойчивостью без вычисления корней.

Критерий устойчивости делятся на: частотные и алгебраические.

Переход от t-преобр к W- преобр:

W-преобр это билинейное уравнение:

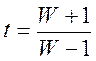W-псевдочастота

Если в x y от переменной t(z) перейти к переменной W, то получится x у относительно W: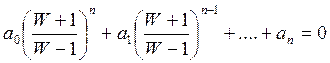

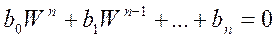
Осуществляется переход от (4) к (5) и для него справедливы все критерии устойчивости.