Определение 9.7. Вектор x евклидова пространства V называется ортогональным подпространству L 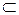 V, если он ортогонален любому вектору из L, т. е.
V, если он ортогонален любому вектору из L, т. е.
x 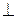 L
L 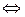 x
x 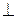 y
y 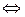 (x, y) = 0,
(x, y) = 0, 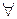 y
y  L.
L.
Если подпространство L порождено векторами y 1, y 2,…, y k, т. е. является линейной оболочкой этих векторов: L = L (y 1, y 2,…, y k), то
x 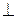 L (y 1, y 2,…, y k)
L (y 1, y 2,…, y k) 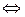 x
x 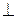 y i, i = 1, 2,..., k.
y i, i = 1, 2,..., k.
Последнее соотношение в R 3 выражает тот известный из элементарной геометрии факт, что вектор перпендикулярен плоскости тогда и только тогда, когда он перпендикулярен любым двум неколлинеарным векторам этой плоскости.
Определение 9.8. Два подпространства L и М пространства V называются ортогональными, если любой вектор подпространства L ортогонален любому вектору подпространства М, т. е.
L 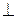 М
М 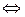 x
x 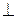 y
y 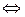 (x, y) = 0,
(x, y) = 0, 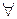 x
x  L,
L, 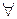 y
y  М.
М.
Если при этом пространства L и М дополнительны друг к другу в V (т. е. V = L + М, L 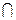 М = 0), то М называется ортогональным дополнением к L и обозначается М =
М = 0), то М называется ортогональным дополнением к L и обозначается М = 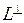 .
.
Из теоремы 8.5 вытекает следующая теорема.
Теоремa 9.3. Евклидово пространство V является прямой суммой подпро-странства L и его ортогонального дополнения, т. е.
V = L + 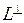
 V = { x = y + z | y
V = { x = y + z | y  L, z
L, z 
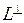 },
},
причем
dim V = dim L + dim 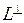 .
.
 2015-08-21
2015-08-21 715
715








