Матрица линейного оператора в заданном базисе

Пусть V – линейное пространство с базисом u ¹, u ², …, u ⁿ, а A – линейный оператор, действующий из V в линейное пространство W размерности т, базисом которого служат векторы v ¹, v ²,…, v ^m. Тогда любой вектор x V представим в виде x = x ₁ u ¹ + x ₂ u ²+…+ x_n u ⁿ. В силу линейности оператора A получаем

Ax = A 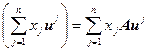. (10.2)

Векторы Au ^j W, j = 1, 2,..., n, однозначно разлагаются по векторам базиса пространства W:

Au ^j = а _{1 j} v ¹+ а _{2 j} v ²+…+ а_mj v ^m = 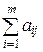v ⁱ, (10.3)

где а _{1 j}, а _{2 j},…, а_mj – координаты векторов Au ^j W. Так как вектор Ax тоже принадлежит W, то аналогично

Ax = у ₁ v ¹+ у ₂ v ²+…+ у_m v ^m = 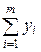v ⁱ, (10.4)

где у ₁, у ₂,…, у_m – координаты вектора Ax W. Из формул (10.2)–(10.4) получаем

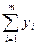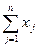
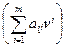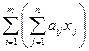v ⁱ = = v ⁱ,

откуда, приравняв коэффициенты при соответствующих векторах v ⁱ, i = 1, 2,..., т, получим систему из т равенств вида

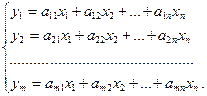
Эти равенства представляют собой формулы для вычисления координат у ₁, у ₂,…, у_m вектора y = Ax при линейном отображении A: V ® W через координаты x ₁, x ₂,…, x_n вектора x V.

Определение 10.9. Из данных равенств следует, что при заданных базисах u ¹, u ²,…, u ⁿ в пространстве V и v ¹, v ²,…, v ^m в пространстве W линейный оператор A: V ® W полностью определяется матрицей

А 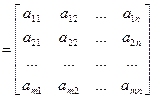, (10.5)

которая называется матрицей линейного оператора A в выбранных базисах.

Столбцами матрицы А, как следует из равенств (10.3) и (10.5), служат координаты векторов Au ¹, Au ²,..., Au ⁿ в базисе v ¹, v ²,…, v ^m пространства W. Строки этой матрицы образуют коэффициенты разложения координат вектора y = Ax по координатам вектора x. В силу единственности разложений векторов по базису матрица А линейного оператора A при фиксированных базисах пространств V и W определяется однозначно. Поскольку умножение матрицы на вектор обладает линейными свойствами, то любую прямоугольную матрицу можно рассматривать как матрицу некоторого линейного оператора.

Таким образом, между множествами матриц и линейных операторов устанавливается взаимно однозначное соответствие.

В силу этого соответствия линейные операторы и их матрицы будем обозначать одними и теми же буквами, т. е. если A – оператор, то А – его матрица.

Таким образом, равенство y = Ax в координатной форме имеет вид

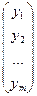
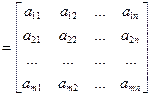
y = 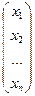= A x. (10.6)

Еще раз отметим, что формула (10.6) устанавливает связь между координатами вектора x V и координатами его образа y = Аx W.

Из равенства (10.6) следует, что область значений im A оператора A совпадает с линейной оболочкой L, порожденной векторами-столбцами матрицы А. Следовательно, ранг линейного оператора равен числу линейно независимых векторов-столбцов его матрицы.

Если пространство W совпадает с пространством V, то матрица линейного оператора A: V ® V (очевидно, квадратная порядка n) имеет вид

А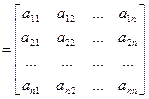

в некотором выбранном базисе u ¹, u ²,…, u ⁿ. Столбцами ее являются координаты векторов Au ^j, j = 1, 2,..., n, в этом базисе.