Моделювання випадкових подій та дискретних випадкових величин

Отримання за допомогою комп’ютера вибіркових значень випадкових величин з різними законами розподілу є важливою умовою для моделювання систем. Самі випадкові величини моделюють за допомогою перетворення одного або декількох незалежних значень випадкової величини, рівномірно розподіленої в інтервалі (0,1). Отримані значення r_i генерують за допомогою програмних генераторів випадкових чисел.

Моделювання незалежних випадкових подій. Змоделюємо настання деякої елементарної події А, ймовірність якої в одному випробуванні дорівнює Р (А) = р. Вважаємо, що умови проведення кожного випробування одинакові і його можна повторити нескінченну кількість разів. Нехай r_i – рівномірно розподілені на інтервалі (0,1) величини, визначені генератором випадкових чисел.

Рис.2.1 Моделювання випадкових подій

Подія А наступить тоді коли 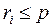, а якщо 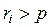, то відбудеться подія . Дійсно, якщо f (r) – функція щільності рівномірно розподіленої випадкової величини r, то

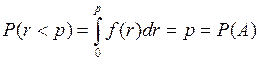(2.6)

Така модель використовується для опису обслуговування вимог у системах масового обслуговування (СМО), пристрій яких може бути вільним або зайнятим, а також для розгалуження інформацій у двох і більше напрямках.

Моделювання несумісних подій. Нехай необхідно дослідити настання групи несумісних подій А ₁, А ₂,..., А_к, з відомими ймовірностями їх настання Р (А ₁), Р (А ₂) ,...,Р (А_к). Зокрема Р (А_і) =р_і, 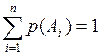, р ₀ =0. На відрізку [0,1] відкладемо значення цих ймовірностей (рис. 2.2).

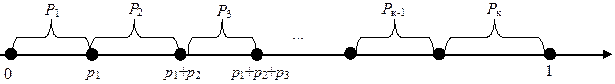
Рис.2.2. Моделювання групи несумісних подій

Попадання в інтервал від 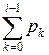до 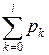випадкових чисел r_i означає, що відбулася подія A_i. Таку процедуру називають визначенням результату випробовування за жеребом. Вона ґрунтується на формулі

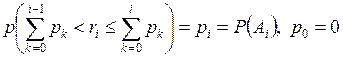(2.7)

Така модель використовується для розгалуження потоків інформації у вузлах мережі, вибору одного з багатьох пристроїв в обслуговуванні СМО, у теорії прийняття рішень, вибору альтернатив у комп’ютерних іграх.

Моделювання складних подій, що залежать від двох і більше (наприклад, m) простих сумісних подій, можна здійснювати двома способами. Перший полягає в послідовній перевірці умови (2.6) для m простих подій, що відповідають m випадковим числам. Другий – у перевірці умови (2.7) для визначення одного з можливих наслідків.

Розглянемо сумісні незалежні події, наприклад, А і В, які мають імовірності настання р_A і р_B. У процесі моделювання можливими наслідками сумісних випробувань будуть чотири події:

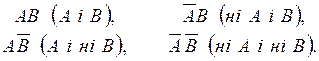
Відповідно їхні імовірності дорівнюють:

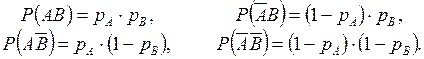
У такій постановці завдання моделювання зводиться до перевірки умови (2.7).

Моделювання сумісних подій. Моделювання сумісних залежних подій, наприклад, А і В, що мають імовірності настання р_А і р_B,полягає в наступному. Вважають, що задана одна з умовних ймовірностей, наприклад, умовна імовірність настання події В за умови, що подія А відбулася Р(В/А). Визначають імовірність можливих подій 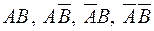з врахуванням того, що ці події складають повну групу подій, тобто

.

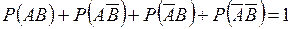Тоді отримаємо:

,

,

,

.

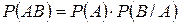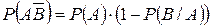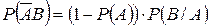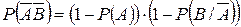Таким чином, задача моделювання зводиться перевірки умови (2.7).

Моделювання випадкової дискретної величини. Розглянемо випадкову дискретну величину Х із заданим законом розподілу (табл. 2.3).

Таблиця 2.3.

Х	Х 1	Х 2	…	Xn
P (X = xi)	p 1	p 2	…	pn

Випадкова величина приймає n значень 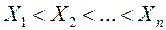з ймовір­ностями 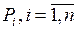, а функція розподілу дорівнює

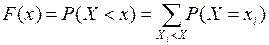. (2.8)

Якщо випадкову величину Х представити як повну групу подій 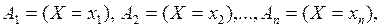то моделювання випадкової дискретної величини виконується аналогічно моделюванню групи несумісних подій.

Тоді функцію розподілу можна записати за допомогою співвідношень:

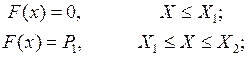
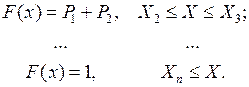
Для моделювання дискретної випадкової величини скористаємося методом оберненої функції [4, 11], суть якого полягає у наступному.

Нехай F(x) – функція розподілу випадкової величини Х, а r – випадкова величина розподілена в інтервалі (0,1). Випадкова величина X отримується розв’язуванням рівняння

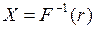, (2.9)

де F^-1 – функція обернена до функції F. Тоді алгоритм обчислення випадкової величини Х, яка задана табл. 2.3 має вигляд:

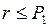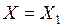якщо , то , інакше

якщ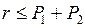о , то 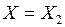, інакше

…

якщ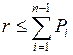о , то 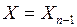, інакше

.

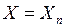Приклад. Нехай дискретна дискретна величина Х має закон розподілу, заданий у табл. 2.4.

Таблиця 2.4.

X	X 1	X 2	X 3
P (X = xi)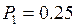

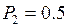
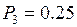
Побудуємо функцію розподілу випадкової величини Х:

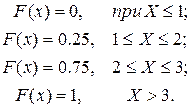
Графік функції розподілу має вигляд (рис. 2.3)

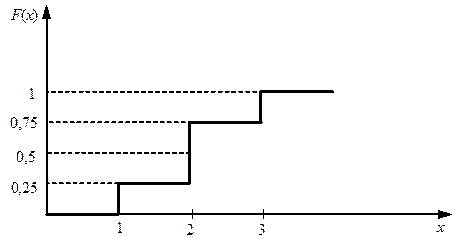
Рис. 2.3. Графік функції розподілу F (x).

Побудуємо графік оберненої функції (рис. 2.4)

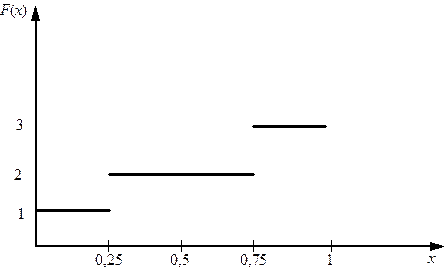
Рис. 2.4. Графік оберненої функції.

Моделювання випадкової величини Х з геометричним розподілом. Задамо її значення та ймовірності у вигляді табл. 2.5.

Таблиця 2.5.

Значення Х			…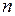
Ймовірність		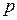p (1 – p)	…	(1 – p) n p

Прикладом випадкової величини з таким розподілом може бути загальна кількість випробувань, які необхідно провести до першого успішного випробування.

Для моделювання випадкової величини з геометричним розподілом можна скористатися методом оберненої функції (2.9). Для великих значень n це вимагає значних затрат комп’ютерного часу. Тому для для отримання значень випадкової величини з геометричним розподілом використовуємо формулу:

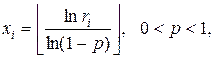(2.10)

де – ціла частину виразу.

Моделювання дискретної випадкової величини з розподілом Бернуллі. Така величина Х приймає тільки два значення: 1 – істина, або 0 – хибність. Такі задачі виникають для моделювання систем з чергами, якщо вихідні потоки і довжини заявок описуються випадковими величиними. Біномінальний розподіл дискретної величини, або розподіл Бернуллі, показує ймовірність настання деякої події за n незалежних повторних випробовувань, у кожному з яких подія настає з ймовірністю p. Ймовірність s успішних подій в n випробовуваннях визначається за формулою

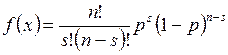. (2.11)

Функція розподілу ймовірностей має вигляд

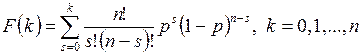(2.12)

Спосіб моделювання випадкової величини з біноміальним розподілом залежить від значення n. Для невеликих значень n випадкова біноміально-розподілена величина визначається як кількість чисел у послідовності { r _i} з n чисел, для яких r_i<p.

Для великих значень n і малих p генеруємо рівномірно розподілені випадкові числа r_i. Алгоритм завершуємо, якщо виконується умова

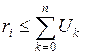, (2.13)

де U ₀ i U_k+1 визначаються формулами:

.

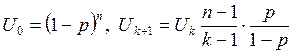Отже, значення випадкової величини з біноміальним розподілом дорівнює кількості випробовувань n. Завершення проведення випробовувань зумовлюється умовою (2.13).