Квантовомеханический случай

В квантовой механике колебания двух ядер в двухатомной молекуле рассматриваются как в классической физике – движение двух масс m ₁ и m ₂ заменяется перемещением одной частицы массой 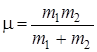и смещаемой из положения равновесия на величину q ₀. Для нахождения полной колебательной энергии E такой частицы необходимо решить уравнение Шрёдингера типа

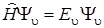, (3.13)

где 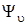– волновая функция гармонического осциллятора, а 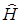– оператор энергии, соответствующий классическому выражению Н (р, q) функции Гамильтона от обобщенных импульсов (р) и обобщенных координат (q)

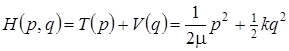. (3.14)

Заменив классическое выражение импульса р его оператором 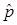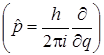, получим

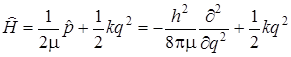. (3.15)

Собственные значения энергии 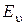и собственные функции 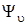этого оператора находим путем решения уравнения вида (3.13) записанного для конкретной рассматриваемой системы

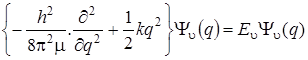
или

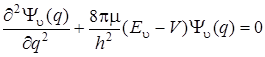. (3.16)

При определенных ограничениях, налагаемых на функцию 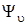(она должна быть однозначной, непрерывной, исчезающей на бесконечности и иметь интегрируемый квадрат модуля), уравнение (3.16) имеет решения при значениях 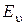полной энергии:

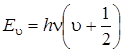, (3.17)

где n – классическая частота колебаний, определяемая формулой

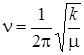[с^–1], (3.18)

а u – колебательное квантовое число, принимающие целые значения
0, 1, 2,... Если выражать полную энергию E_u в см^–1, то равенство (3.17) можно записать, опуская h, т. е.

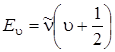, (3.19)

где 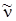– волновое число (частота колебаний, выраженная в см^–1).

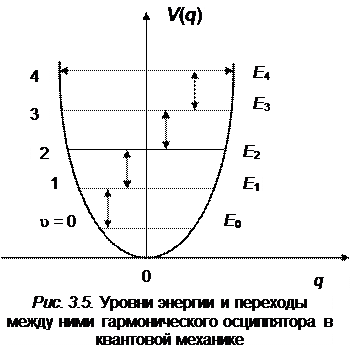
Формула (3.17) дает равностоящие невырожденные уровни энергии (см. рис. 3.5). Согласно правилу отбора для гармонического осциллятора разрешены все переходы с изменением колебательного квантового числа на единицу, т. е. 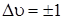. Таким образом, в спектре ИК-поглощения и испускания могут комбинировать между собой только соседние энергетические уровни, разность энергий которых определяется формулой:

E _u₊₁ – E _u = h n, (3.20)

а частота соответствующего перехода между этими уровнями равна

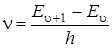[c^–1]

или

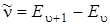[cм^–1]. (3.21)

и совпадает с частотой классического осциллятора .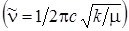

Итак, квантовомеханический осциллятор обладает дискретным равноотстоящим набором значений энергии. Классический осциллятор, наоборот, обладает непрерывным набором значений энергии, зависящим от амплитуды колебаний. Далее. Если минимальное значение энергии классического осциллятора равно нулю, то минимальная энергия гармонического осциллятора в квантовой механике отлична от нуля и равна

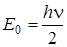[Дж]

или

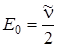[cм^–1], (3.22)

т. е. молекула в основном колебательном состоянии 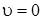обладает определенной нулевой энергией. Это значение энергии не так уж мало, особенно для легких молекул типа Н₂ (частота колебаний 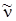молекулы Н₂ равна 4401 см^–1), и его необходимо учитывать при расчете некоторых термодинамических постоянных на основе данных ИК-спектров.

Рассмотрим соответствие между классическим и квантовомеханическим осцилляторами. Для этого проанализируем выражения для собственных волновых функций квантовомеханического осциллятора, которые в общем виде записываются следующим образом:

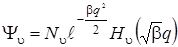, (3.23)

где N _u – нормировочный множитель, равный

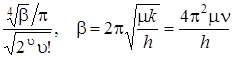а 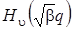) – полином Чебышева Эрмита степени 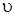относительно q.

Первые четыре полинома Чебышева – Эрмита равны следующим выражениям при :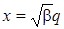

Н ₀ (х) = 1, H ₁(х) = 2 х, Н ₂(х) = 4 х ² – 2,

Н ₃ (х) = 8 х ³ – 12 х.

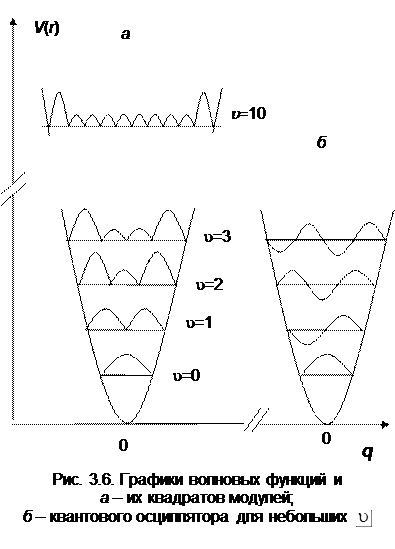
Наличие множителя 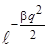в функции (3.23) приводит к быстрому ее спаду (уменьшению за пределами области классического движения). Число узлов функции (3.23) равно числу нулей полиномов Чебышева-Эрмита, равных u. Вид волновых функций 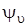для малых u, а также их квадратов 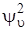(или 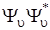) приведены на рис. 3.6. Каждый график построен на прямой, изображающей соответствующий уровень энергии. Слева на этом рисунке показана зависимость квадрата волновой функции (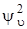) от 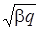, определяющего вероятность различных значений координаты. В случае нулевого колебательного состояния (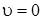) функция 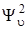с точностью до нормирующего множителя выражается формулой 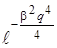, т. е. представляет собой функцию ошибок Гаусса. Она имеет максимум при q = 0. Для возбужденных состояний (u = 1, 2, ….), получается ряд максимумов, причем наибольшая вероятность колебательной координаты получается вблизи поворотных точек классического движения. Чем больше u, тем ближе общий характер квантовомеханического распределения вероятности как функции колебательной координаты к соответствующему распределению, получающемуся на основе классической теории. Отличие состоит в том, что в квантовой механике за пределами классического движения вероятность нахождения системы отлична от нуля, хотя и быстро убывает при изменении q.