return to section 1.2.1
Table 1
Types of Evidence of A Capacity Limit of About 4 Items, With Selected Key References (Numbered According to the Relevant Section of the Article)
3.1. Imposing an Information Overload
3.1.1. Visual whole report of spatial arrays (Sperling, 1960)
3.1.2. Auditory whole report of spatiotemporal arrays (Darwin et al. 1972)
3.1.3. Whole report of unattended spoken lists (Cowan et al., in prep.)
3.2. Preventing Long-term Memory Recoding, Passive Storage, and Rehearsal
3.2.1. Short-term, serial verbal retention with articulatory suppression (see Table 3 references; also Pollack et al., 1959; Waugh & Norman, 1965)
3.2.2. Short-term retention of unrehearsable material (Glanzer & Razel, 1974; Jones et al., 1995; Simon, 1974; Zhang & Simon, 1985)
3.3. Examining Performance Discontinuities
3.3.1. Errorless performance in immediate recall (Broadbent, 1975)
3.3.2. Enumeration reaction time (Mandler & Shebo, 1982; Trick & Pylyshyn, 1993)
3.3.3. Multi-object tracking (Pylyshyn et al., 1994)
3.3.4. Proactive interference in immediate memory (Halford et al., 1988; Wickelgren, 1966)
3.4. Examining Indirect Effects of the Limits
3.4.1. Chunk size in immediate recall (Wickelgren, 1964; Ryan, 1969; Chase & Simon, 1974; Ericsson et al., 1980; Ericsson, 1985)
3.4.2. Cluster size in long-term recall (Broadbent, 1975; Graesser & Mandler, 1978)
3.4.3. Positional uncertainty in recall (Nairne, 1991)
3.4.4. Analysis of the recency effect in recall(Watkins, 1974)
3.4.5. Sequential effects in implicit learning and memory (Cleeremans & McClelland, 1991; McKone, 1995)
3.4.6. Influence of capacity on properties of visual search (Fisher, 1984)
3.4.7. Influence of capacity on mental addition reaction time (Logan, 1988; Logan & Klapp, 1991)
3.4.8. Mathematical modeling parameters (Kintsch & van Dijk, 1978; Raaijmakers & Shiffrin, 1981; Halford et al., 1998
3.1. Capacity limits estimated with information overload. One way in which long-term recoding or rehearsal can be limited is through the use of stimuli that contain a large number of elements for a brief period of time, overwhelming the subject's ability to rehearse or recode before the array fades from the time-limited buffer stores. This has been accomplished in several ways.
3.1.1. Visual whole report of spatial arrays. One study (Sperling, 1960) will be explained in detail, as it was among the first to use the logic just described. It revealed evidence for both (a) a brief, pre-attentive, sensory memory of unlimited capacity and (b) a much more limited, post-attentive form of storage for categorical information. Sperling's research was conducted to explore the former but it also was informative about the latter, limited-capacity store. On every trial, an array of characters (e.g., 3 rows with 4 letters per row) was visually presented simultaneously, in a brief (usually 50-msec) flash. This was followed by a blank screen. It was assumed that subjects could not attend to so many items in such a brief time but that sensory memory outlasted the brief stimulus array, and that items could be recalled to the extent that the information could be extracted from that preattentive store. On partial report trials, a tone indicated which row of the array the subject should recall (in a written form), but on whole report trials the subject was to try to recall the entire array (also in written form). The ability to report items in the array depended on the delay of the partial report cue. When the cue occurred very shortly after the array, most or all of the 4 items in the cued row could be recalled, but that diminished as the cue delay increased, presumably because the sensory store decayed before the subject knew which sensory information to bring into the more limited, categorical store.
By the time the cue was 1 sec later than the array, it was of no value (i.e., performance reached an asymptotically low level). Subjects then could remember about 1.3 of the cued items from a row of 4. It can be calculated that at that point the number of items still remembered was 1.3 x 3 (the number of rows in the array) or about 4. That was also how many items subjects could recall on the average on trials in the "whole report" condition, in which no partial report cue was provided. The limit of 4 items was obtained in whole report across a large variety of arrays differing in the number, arrangement, and composition of elements. Thus, a reasonable hypothesis was that subjects could read about 4 items out of sensory memory according to a process in which the unlimited-capacity, fading sensory store is used quickly to transfer some items to a limited-capacity, categorical store (according to the present theoretical framework, the focus of attention).
One could illustrate the results of Sperling (1960) using Figure 1, which depicts the interaction of nested faculties in the task in a manner similar to Cowan (1988, 1995). Within that theoretical account, sensory memory is assumed to operate through the activation of features within long-term memory (an assumption that has been strengthened through electrophysiological studies of the role of reactivation in automatic sensory memory comparisons; see Cowan, Winkler, Teder, & Näätänen, 1993). The nesting relation implies that some, but not all, of sensory memory information also is in the focus of attention at a particular moment in this task. In either the whole report condition or the partial report condition, the limited capacity store (i.e., the focus of attention) can be filled with as many of the items from sensory memory as the limited capacity will allow; but in the partial report condition, most of these items come from the cued row in the array. Because the display is transient and contains a large amount of information, subjects have little chance to increase the amount recalled through mnemonic strategies such as maintenance or elaborative rehearsal. Part A of the figure represents whole report and shows that a subset of the items can be transferred from activated memory to the capacity-limited store. Part B of the figure, representing partial report, shows that the items transferred to the capacity-limited store are now confined to the cued items (filled circles), allowing a larger proportion of those items to be reported.
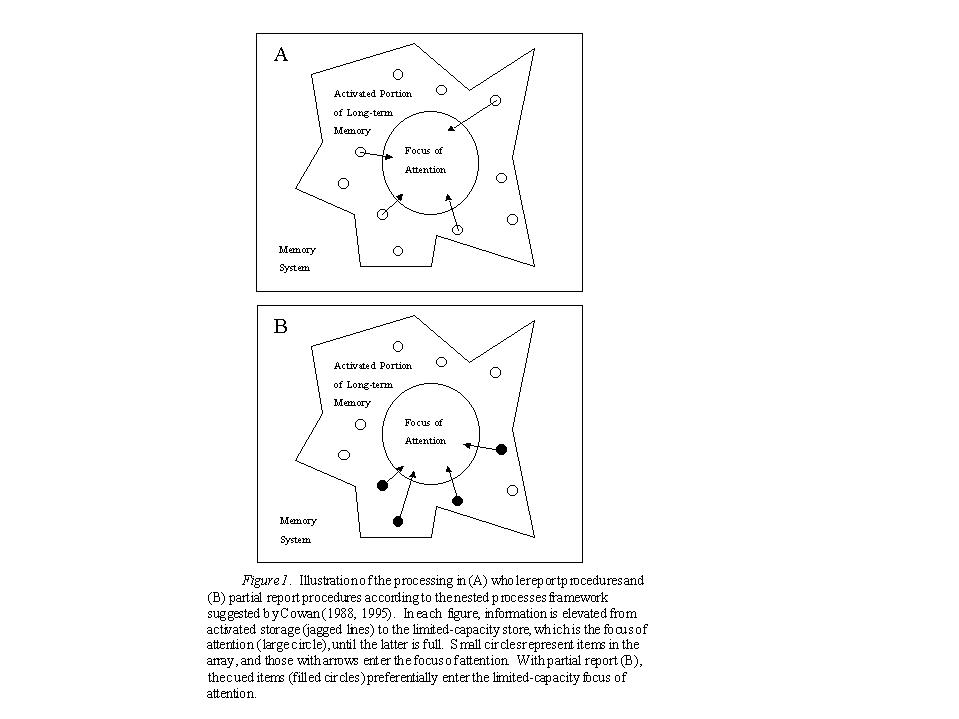
A word is in order about the intent of this simple model shown in Figure 1. It is not meant to deny that there are important differences between more detailed structures such as the phonological store and the visuospatial sketch pad of Baddeley (1986). However, the model is meant to operate on a taxonomically inclusive level of analysis. It seems likely that there are other storage structures not included in Baddeley's model, such as memory for nonverbal sounds and for tactile stimuli. In principle, moreover, these separate structures could share important functional properties (e.g., incoming stimuli requiring a particular kind of coding interfere with the short-term retention of existing representations using similar coding) and could operate based on similar neural mechanisms of activation. Given that we do not know the taxonomy of short-term stores, they are represented together in the model according to their common principle, that they are activated portions of the long-term memory system. This activated memory includes both physical features and conceptual features. What is critical for the present purposes is that all of the storage structures making up activated memory are assumed not to have capacity limitations. Instead, they are assumed to be limited because of memory decay, interference from subsequent stimuli, and/or some other basis of temporary accessibility. Only the focus of attention is assumed to have a fixed capacity limit in chunks, and it is that capacity limit that is of primary concern here.
There are also a number of other theoretical suggestions that are consistent with the present approach but with different terminology and assumptions. For example, the approach appears compatible with a model proposed recently by Vogel, Luck, and Shapiro (1998). Their "conceptual short-term memory" would correspond to the activated portion of long-term memory in the model of Cowan (1988), whereas their "visual working memory" would correspond to the focus of attention. Potential differences between the approaches appear to be that what they call conceptual memory could, according to Cowan (1988), include some physical features; and what they call visual working memory would, according to Cowan (1988), prove to be one instance of the focus of attention, a central structure that represents conscious information from all modalities. The most critical similarity between the models for present purposes is that the capacity limit shows up in only one place (the visual working memory or focus of attention), not elsewhere in the model.
With these theoretical points in mind, we can return to a consideration of Sperling's study. The observed limit to about 4 items in whole report theoretically might be attributed to output interference. However, studies by Pashler (1988) and Luck and Vogel (1997), in which output interference was limited, militate against that interpretation. In one experiment conducted by Luck and Vogel, for example, subjects saw an array of 1 to 12 small colored squares for 100 msec and then, after a 900-msec blank interval, another array that was the same or differed in the color of one square. The subject was to indicate whether the array was the same or different. Thus, only one response per trial was required. Performance was nearly perfect for arrays of 1-3 squares, slightly worse with 4 squares, and much worse at larger array sizes. Very similar results were obtained in another experiment in which a cue was provided to indicate which square might have changed, reducing decision requirements. Some of their other experiments clarify the nature of the item limit. The 4-item limit was shown to apply to integrated objects, not features within objects. For example, when objects in an array of bars could differ on four dimensions (size, orientation, color, and presence or absence of a central gap), subjects could retain all four dimensions at once as easily as retaining any one. The performance function of proportion correct across increasing array size (i.e., increasing number of array items) was practically identical no matter how many stimulus attributes had to be attended at once. This suggested that the capacity limit should be expressed in terms of the number of integrated objects, not the number of features within objects. The objects serve as the chunks here.
Broadbent (1975) noted that the ability to recall items from an array grows with the visual field duration: "for the first fiftieth of a second or so the rate of increase in recall is extremely fast, and after that it becomes slower." He cites Sperling's (1967) argument that in the early period, items are read in parallel into some visual store; but that, after it fills up, additional items can be recalled only if some items are read (more slowly) into a different, perhaps articulatory store. Viewed in this way, the visual store would have a capacity of 3 to 5 items, given that the performance function rapidly increases for that number of items. However, the "visual store" could be a central capacity limit (assumed here to be the focus of attention) rather than visually specific as the terminology used by Sperling seems to imply.
A related question is what happens when access to the sensory memory image is limited. Henderson (1972) presented 3 x 3 arrays of consonants, each followed by a masking pattern after 100, 400, 1000, or 1250 msec. This was followed by recall of the array. Although the number of consonants reported in the correct position depended on the duration of the array, the range of numbers was quite similar to other studies, with means for phonologically dissimilar sets of consonants ranging from about 3 with 100-msec exposure times to about 5.5 with 1250-msec exposure times. This indicates that most of the transfer of information from sensory storage to a limited-capacity store occurs rather quickly.
A similar limit may apply in situations in which a scene is changed in a substantial manner following a brief interruption and people often do not notice the change (e.g., Simons & Levin, 1998). Rensink, O'Regan, and Clark (1997) proposed that this limit may occur because people can monitor only a few key elements in a scene at one time.
3.1.2. Auditory whole report of spatiotemporal arrays. Darwin, Turvey, and Crowder (1972) carried out an experiment that was modeled after Sperling's (1960) work, but with stimuli presented in the auditory modality. On each trial, subjects received 9 words in a spatiotemporal array, with sequences of 3 spoken items (numbers and letters) presented over headphones at left, center, and right locations simultaneously for a total array size of 9 items. The partial report cue was a visual mark indicating which spatial location to recall. The results were quite comparable to those of Sperling (1960). Once more the partial report performance declined across cue delays until it was equivalent to the whole report level of about 4 items though, in this experiment in the auditory modality, the decline took about 4 sec rather than 1 sec as in vision, and the last item in each sequence was recalled better than the first two items. In both modalities, the whole report limit may suggest the limited capacity for storage of item labels in a consciously accessed form.
3.1.3. Whole report of ignored (unattended) spoken lists. In all of the partial report studies, the measure of short-term memory capacity depended upon the fact that there were too many simultaneously presented items for all of them to be processed at once, so that the limited-capacity mechanism was filled with items quickly. If items were presented slowly and one at a time, the subject would be able to use mnemonic processes such as rehearsal (e.g., Baddeley, 1986) to expand the number of items that could be held, and therefore would be able to exceed the constraints of the limited-capacity store. If a way could be found to limit these mnemonic processes, it could allow us to examine pure capacity in a test situation more similar to what is ordinarily used to examine STM (presumably yielding a compound STM estimate); namely immediate, serial verbal list recall.
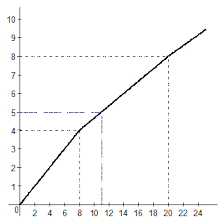
Cowan et al. (1999) limited the processing of digits in a spoken list by having subjects ignore the items in the spoken list until after their presentation. Subjects played a computer game in which the name of a picture at the center of the screen was to be compared to the names of four surrounding pictures to indicate (with a mouse click) which one rhymed with the central picture. A new set of pictures then appeared. As this visual game was played repeatedly, subjects ignored lists of digits presented through headphones. Occasionally (just 16 times in a session), 1 sec after the onset of the last spoken word in a list, the rhyming game disappeared from the screen and a memory response screen appeared shortly after that, at which time the subject was to use the keypad to report the digits in the spoken list. Credit was given for each digit only if it appeared in the correct serial position. Relative to a prior memory span task result, lists were presented at span length and at lengths of span-1 (i.e., lists one item shorter than the longest list that was recalled in the span task), span-2, and span-3. A control condition in which subjects attended to the digits also was presented, before and after the ignored-speech session. In the attended-speech control condition, the number of digits recalled was higher than in the unattended condition, and it increased with list length. However, in the ignored-speech condition, the mean number of items recalled remained fixed at a lower level regardless of list length. The level was about 3.5 items in adults, and fewer in children. This pattern is reproduced in Figure 2. It is important that the number correct remained fixed across list lengths in the ignored-speech condition, just as the whole-report limit remained fixed across array sizes in Sperling (1960). It is this pattern that is crucial for the conclusion that there is a fixed capacity limit.
return to section 3.3.4

It is important also to consider individual-subject data. Sperling's (1960) data appeared to show that his very few, highly trained individuals had capacity limits in the range of about 3.5 - 4.5. In the study of Cowan et al. (1999), results from 35 adults are available even though only the first 24 of these were used in the published study. Figure 3 shows each adult subject's mean number correct in the unattended speech task, as well each subject's standard error and standard deviation across unattended speech trials. It is clear from this figure that individuals did not fit within a very narrow window of scores; their individual estimates of capacity ranged from as low as about 2 to as high as almost 6 in one participant. One might imagine that the higher estimates in some individuals were due to residual attention to the supposedly ignored spoken digits, but the results do not support that suggestion. For example, consider the subject shown in Figure 3 who had the best memory for ignored speech. If that subject attended to the spoken digits that were to be ignored, then the result should have been a positive slope of memory across the four list lengths, similar to the attended-speech condition shown in Figure 2. In fact, however, that subject's scores across 4 list lengths had a slope of -0.35. Across all of the adult subjects, the correlation between memory for ignored speech and slope of the ignored speech memory function was r = -.19, n.s. The slight tendency was thus for subjects with better recall to have less positive slopes than those with poorer recall. The slopes were quite close to zero (M = 0.05, SD = 0.32) and were distributed fairly symmetrically around 0. Another possible indication of attention to the supposedly ignored speech would be a tradeoff between memory and visual task performance during the ignored speech session. However, such a tradeoff did not occur. The correlation between memory for unattended speech and reaction times on the visual task was -.33, n.s., the tendency being for subjects with better memory for ignored speech also to display slightly shorter reaction times on the visual task. The same type of result was obtained for the relation between memory and visual task reaction times on a trial-by-trial basis within individuals. The mean within-subject correlation was -.08 (SD =.25), showing that the slight tendency was for a subject's trials that produced better memory to be accompanied by shortermean reaction times on the preceding visual task. Thus, the memory capacity of up to 6 items in certain individuals as measured in this technique and the individual differences in capacity seem real, not due to attention-assisted encoding. Figure 3 shows that individuals' standard errors (rectangles) were relatively small, and that even the standard deviations (bars) of the best versus the worst rememberers did not overlap much.
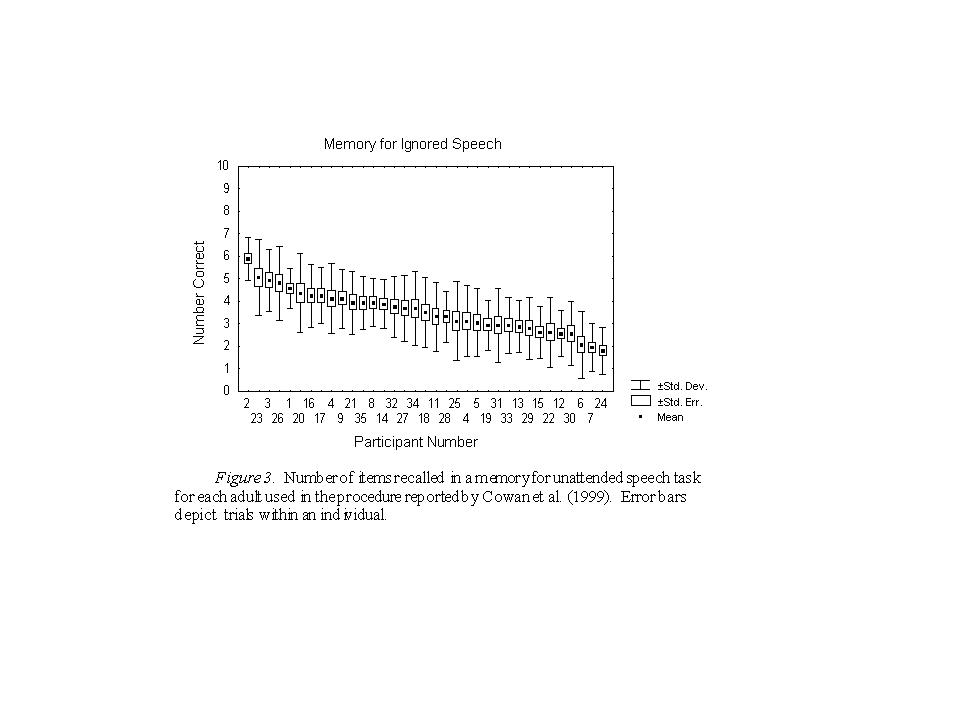
The study of Cowan et al. (1999) is not the only one yielding individual difference information. For example, the data set reported as the first experiment of Luck and Vogel (1997), on visual storage capacity, resulted from individual subject estimates of storage capacity ranging from 2.2 to 4.7, and a graduate student who spent months on the capacity-estimation tasks developed a capacity of about 6 items (Steven Luck, personal communication, January 18, 1999). These estimates are quite similar to the ones shown in Figure 3 despite the great differences in procedures. Similar estimates can be obtained from the study of Henderson (1972), in which each consonant array was followed by a mask. For example, with a 400-msec field exposure duration (long enough to access sensory memory once, but probably not long enough for repeated access) and no supplementary load, the 6 subjects' mean number correct ranged from 3.0 to 5.1 items.
All of these results appear to require a modification of conclusions that could be drawn from the previous literature. In his ground-breaking review of memory span, Dempster (1981, p. 87) concluded that "there is little or no evidence of either individual or developmental differences in capacity." In the previous literature only processing speeds were found related to span, but none of the previous developmental investigations examined memory with strategic processing during reception of the list minimized so as to examine capacity. There do appear to be individual and developmental differences in capacity.
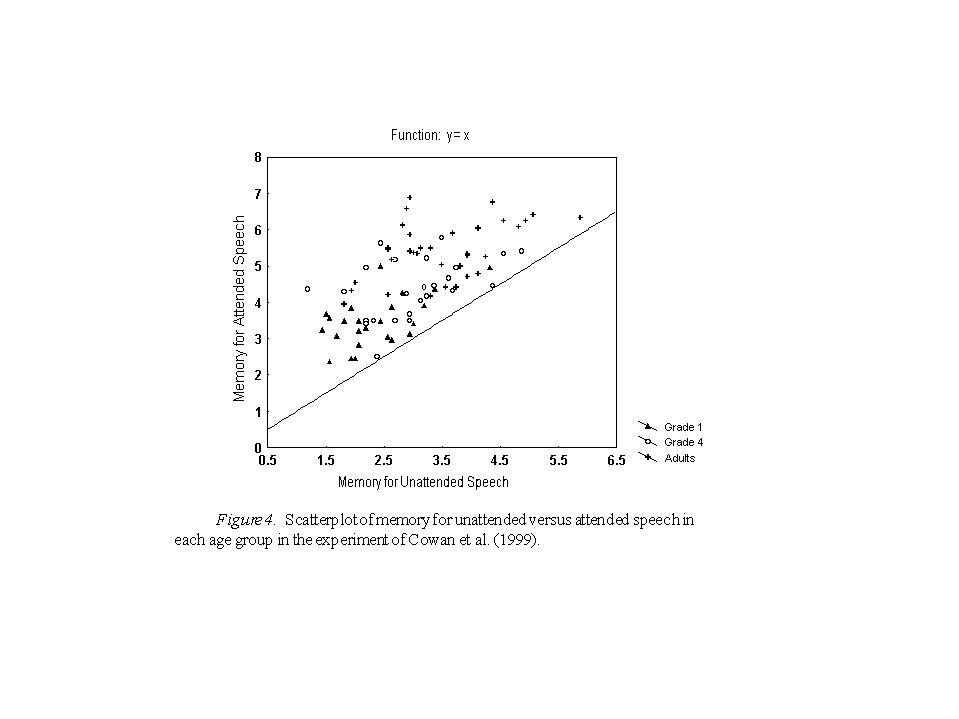
Figure 4 illustrates another intriguing point about Cowan et al. (1999). In this scatterplot of memory for unattended versus attended speech in individuals within each age group, the equation line represents the case in which memory was equal in the two tasks. What the plot shows is that memory was always better in the attended speech task, but that the amount of improvement in the attended speech task relative to the unattended speech task was independent of the level of performance on the unattended task. In the attended condition the means (and SDs) were: for 35 adults, 5.43 (0.78); for 26 fourth graders, 4.31 (0.88); and for 24 first graders, 3.48 (0.69). In the ignored speech condition the comparable means were: for the adults, 3.51 (0.94); for the fourth graders, 2.99 (0.86); and for the first graders, 2.34 (0.69). Notice that, among all groups, the ratio of mean attended to unattended numbers correct fell within a narrow range, between 1.4 and 1.6. This pattern suggests that attention at the time of reception of the list may add a process that is independent of the processes involved in memory for unattended speech. That process presumably is independent of the pure capacity limit and could reflect the use of attention to form larger chunks.
return to section 4.1.4
It should be noted that the main scoring procedure used by Cowan et al. (1999) credited correct recall of a digit only if it appeared in the correct serial position. Cowan et al. also examined results of a scoring procedure in which credit was given for any correct digit, regardless of the serial position. Such results cannot be compared across list lengths because the probability of guessing correctly increases dramatically with list length (given that each digit could occur only once per list). Nevertheless, it is noteworthy that recall at all ages was more like a constant proportion correct across lists lengths in this free scoring, not a constant number correct as in the serial position scoring. Adults and fourth-grade children were over 90% correct on lists of length 4 through 6, the lengths examined with this scoring procedure, and first-grade children were correct on 83%, 80%, and 83% of the lists at these three lengths. The item scoring raises the question of what it is that is held in a capacity-limited mechanism. It cannot simply be the items that are held, as the free scoring does not show the limited-capacity pattern of a constant number correct across list lengths. The digits themselves may be stored in activated memory (e.g., auditory sensory or phonological memory) and drawn from it into the focus of attention as needed. Instead, it might be the mapping between the digits in memory and the serial positions in the list that would have to be held in capacity-limited storage.
3.2. Capacity limits estimated by blocking long-term memory recoding, passive storage, and rehearsal. Verbal materials can be used under conditions that discourage recoding and rehearsal, or materials that are intrinsically difficult to recode, store, and rehearse can be used. These methods force subjects to rely primarily on capacity-limited storage of chunks that were learned out of the laboratory or, at least, before the experimental trial in question.
3.2.1. Short-term, serial verbal retention with articulatory suppression. The contribution of long-term memory can be minimized by drawing the stimuli from the same, small set on every trial and requiring the correct recall of serial order. Because the same items recur over and over, it is difficult to retain long-term associations that help in the retention of serial order of the items on a particular trial. That is, in fact, the nature of the stimuli in most immediate, serial recall experiments that have been conducted. Further, the contribution of rehearsal can be minimized by imposing articulatory suppression (Baddeley, 1986; Murray, 1968), a secondary task in which the subject repeats, whispers, or mouths a rote utterance over and over during the presentation of items (e.g., "the, the, the...") and sometimes throughout recall itself if a nonspeech recall mode is used.
Cowan, Wood et al. (1998) offered an account of what these variables do when used together. They proposed that when new words are presented on every trial in a serial recall task, the phonological portion of activated memory includes a phonological representation of the word sequence. However, when the same words are used over and over on every trial, all of the representations of items from the memory set become active in memory, so that the memory items in the current list cannot necessarily be distinguished from items used in previous trials. Rehearsal may allow a special representation of the to-be-recalled list to be constructed in active memory even under these circumstances in which a small set of items is used over and over. Cowan, Wood et al. offered these assumptions to account for why articulatory suppression has a much larger effect on performance for a small set of words than for large sets of words that are not repeated from trial to trial. A small set of words used over and over, along with articulatory suppression, may minimize the contribution of articulatory and passive phonological storage factors in recall. It is only under these conditions, for example, that the "word length effect," or advantage for lists composed of short words, is eliminated (LaPointe & Engle, 1990). Word length effects that remain even with articulatory suppression when a large set of items is used can be explained on the grounds that phonological representations of these items are generated from long-term memory (Besner, 1987) and remain active despite articulatory suppression. (An alternative interpretation of articulatory suppression effects would state that suppression works by taking up processing capacity rather than by blocking rehearsal. However, if that were true, suppression should impair performance even when a large set of words is used. Given that it does not, the alternative interpretation seems wrong.)
Before describing results of serial recall experiments with spoken stimuli and articulatory suppression, it is necessary to restrict the admissible serial recall data in a few other ways. Memory for multisyllabic words was excluded because these often might be retained as separate segments rather than integrated units (e.g., fire-man if morphemic segments are used; um-brel-la if syllabic segments are used). Memory for nonwords also was excluded because one might retain them in terms of separate phonemic or syllabic series even if they are monosyllabic. Only spoken words were included because articulatory suppression seems to interfere with the retrieval of the phonological representation of printed words, but not of spoken words. For example, articulatory suppression during the presentation of a list eliminates phonological similarity effects for printed words, but not for spoken words (Baddeley, Lewis, & Vallar, 1984). Finally, conditions with highly unusual stimulus parameters were eliminated. Unusually slow stimulus presentations (> 4 sec per word) were excluded because it might be possible to insert rehearsals despite the articulatory suppression, as were unusually fast presentations (< 0.5 sec per word) because of encoding difficulty; and grouped presentations were omitted because they encourage long-term recoding of the list.
Table 2 shows the results for all studies meeting these constraints. I was able to find 9 studies that included at least one experimental condition involving the immediate recall of spoken, monosyllabic words from a small set in the presence of articulatory suppression. Among these studies I was able to derive 17 independent estimates of memory storage. There appears to be a striking degree of convergence among the 17 estimates. All but one of the estimates fell within the range of 3-5 items, and most fell in the 3-4-item range. The only outlier was an estimate of 2.4 items from Longoni et al. (1993). That low estimate is difficult to understand because the stimulus conditions were almost identical to another experimental condition in Longoni et al. that yielded an estimate of 3.4 items.
return to section 3.2.2
return to section 4.3.7
Table 2
Estimates of Capacity from Studies of Immediate Verbal Memory With Auditory Presentation and Articulatory Suppression
| Reference | Data Source | Method of Calculating Items in Storage | Est. |
| Murray (1968) | Figure 1, p. 682. Cued recall; auditory presentation with suppression. 6 letters. | Add the proportions correct across probed serial positions and assume recall of the first, unprobed item in the list =.8. Thus, at List Length 6:.4+.2+.4+.5+.8=2.3; +1=3.3. | 3.1 |
| same | 7 letters | same | 3.2 |
| same | 8 letters | same | 3.0 |
| same | 9 letters | same | 3.1 |
| Peterson & Johnson (1971) | Table 2, p. 349 (5 letters, serial recall; count during pres., low-similarity condit.) Date = proportion of lists recalled correctly. | 5 items, 45% of lists correct. High assumption is that on the other 55% of trials, subjects get 4 correct, for a mean of 5(.45) + 4(.55) = 4.45. A more moderate assumption is 5(.45) + 4(.28) + 3(.27) = 4.18. | 4.2 |
| Levy (1971) | Table 1, p. 126. Neutral arctic. cond., cued recall, simultan. auditory presentation 7 serial positions | 7 ser. posit. x.39 items/s.p. = 2.73 items correct. Add 0.8 items for the first, unprobed position = 3.53 items. | 3.5 |
| same | Table 2, p. 130 9 serial positions | 9 ser. posit. x.34 = 3.06, add 0.8 for first, unprobed position = 3.86 items. | 3.9 |
| Baddeley, Thomson, & Buchanan (1975) | Figure 6, p. 585 Serial recall, monosyllabic words, auditory presentation with suppression | 5 serial positions x.7 items / s.p. correct = 3.5 items. | 3.5 |
| Baddeley, Lewis, & Vallar (1984) | Table 1, p. 236 Serial recall, monosyllabic words, dissimilar items with suppression) Fast presentation | 5 serial positions x.64 items / s.p. correct =3.2 items in each case. | 3.2 |
| Table 2, continued | |||
| same | Slower presentation | same | 3.2 |
| Cowan, Cartwright, Winterowd, & Sherk (1987) | Table 1, p. 514 Monosyllabic words, serial recall, span procedure, dissimilar items with articulatory suppression. Arctic. task: Whisper alphabet | Span = estimate. (Omitted conditions in which articulatory suppression task was presumably ineffective; whisper same letter once after each item, span = 4.81; whisper same letter continuously throughout study, span = 4.86.) | 4.0 |
| same | Task: Whisper next letter on each trial. | same | 4.0 |
| Longoni, Richardson, & Aiello (1993) | Table 3, p. 17 Serial recall, distinct items, suppression task = whisper "the." Presentation rate of 0.5 sec per item. | 6 serial positions x.57 correct = 3.42 (Additional data from a very slow presentation rate of 5 sec per item condition were omitted because rehearsal was possible; for that cond., 6 serial positions x.78 correct = 4.68) | 3.4 |
| same | Table 4, p. 19 Whisper "hiya" during presentation & recall | 6 serial positions x.40 correct = 2.40 It is not clear why such discrepant results obtained in these 2 experiments. | 2.4 |
| Avons, Wright, & Pammer (1994) | Table 1, p. 215 Short words, immediate recall (all had suppression) Serial recall condition | 5 serial positions x.69 items / s.p. correct = 3.45 items. | 3.5 |
| same | Probed recall condition (Probed by the serial position of the item) | 5 serial positions x.72 items / s.p. correct = 3.60 items. | 3.6 |
| Hitch, Burgess, Towse, & Culpin (1996) | Figure 4, p. 125 Auditory presentation of items, suppression, recall in correct serial positions. | Dependent measure = items correct = about 4.0. (Omitted results for grouped lists, about 6.0.) | 4.0 |
The methods of estimation are described briefly in Table 2. The most commonly applicable method was to take the proportion correct at each serial position (or, when necessary, an estimate of this proportion based on a figure) and add the proportions across serial positions to arrive at the number correct. In a probed recall experiment (e.g., Murray, 1968) there is an initial list item for which the procedure produces no memory estimate; based on past research on primacy effects, the available proportion at this first serial position always was estimated at 0.8. For some studies, alternative assumptions led to alternative estimates of storage. For example, in the study of Peterson and Johnson (1971), the dependent measure reported was the number of lists recalled correctly, and to estimate items recalled one must make assumptions about the number of errors within the lists recalled incorrectly. Estimates of capacity are given in the table under a "high" assumption that at least 4 items were recalled within each 5-item list, and under a more "moderate" assumption that erroneous lists contained 1 or 2 errors (i.e., 4 or 3 correct items) equally often. It is the more moderate estimate that appears in the rightmost column of the table. When the measure was memory span, the estimate was taken as the span in conditions in which the articulatory suppression task can be presumed to have been most effective (e.g., in Cowan et al., 1987).
Waugh and Norman (1965) impeded rehearsal in a different way, through instructions to the subjects not to rehearse. In their experiment, each list contained 16 spoken digits and the last digit was accompanied by a tone. It was to serve as a probe, the same digit having occurred once before somewhere in the list. The subject was to respond with the digit that had followed the probe digit when it was presented earlier, in the list. Results with an ordinary, 1-per-sec presentation rate (e.g., Waugh & Norman, 1965, p. 91) showed that performance levels were much higher with 3 or fewer items intervening between the target pair and the response (>.8) than it was with 4 or more intervening items (<.6). The transition between 3 and 4 intervening items was abrupt. Note that with 3 intervening items in this task, successful performance would require that the subject's memory extend back far enough to remember 4 items: the target pair and two intervening items. (The last intervening item was the probe, which did not have to be remembered.) Thus, this task leads to an estimate of 4 items in capacity-limited short-term storage. (Performance levels with a very fast, 4-per-sec presentation decreased rather more continuously as a function of the number of intervening items, which possibly could reflect the heavier contribution of a time-limited source of activation, such as sensory memory, that was the most vivid for more recent items and faded gradually across items.)
Another way to limit rehearsal is to use a "running memory span" procedure, in which a long list of items is presented and the subject is unaware of the point at which the test is to begin. Pollack, Johnson, and Knaff (1959) devised such a procedure. In their Experiment 1, lists of 25, 30, 35, and 40 digits were presented. When the list ended, the task was to write down as many of the most recent items as possible, making sure to write them in the correct serial positions with respect to the end of the list. Under these conditions, the list was too long and continuous for rehearsal to do any good, and the obtained mean span was 4.2 digits. (Theoretically, it might be possible for the subejct continually to compute, say, what were the last 5 items; but there is no task demand that would encourage such difficult work even if it were feasible. The absence of on-line task requirements makes this task very different from the n-back tasks, which, as discussed earlier, do not meet the criterial for inclusion.)
It is possible to prevent rehearsal in yet another way, by requiring processing between items rather than during the presentation of items. Consider, for example, the working memory span task of Daneman and Carpenter (1980) in which the subject must read sentences and also retain the final word of each sentence. The reading should severely limit rehearsal of the target words. Daneman and Carpenter (1980, p. 455) reported a mean span of 3.15 words in this circumstance. It is at first puzzling to think that subjects could do this well, inasmuch as they might need some of the capacity-limited storage space for processing the sentences (unless storage and processing demands are totally separate as suggested by Daneman and Carpenter, 1980 and by Halford et al., 1998). Notice, however, that the word memory load does not reach 3 until after the third sentence has been processed. This might well leave some of the limited storage capacity available for sentence processing until the very end of the trial.
3.2.2. Short-term retention of unrehearsable material. A second way that time-limited stores can be eliminated from a measure of storage is with materials that, by their nature, cannot be rehearsed and thereby refreshed in active memory. It is unlikely that items that cannot be rehearsed lend themselves easily to long-term recoding, either. An analysis of one early study illustrates this distinction. Some verbal materials are too long to be rehearsed (Baddeley, 1986). Simon (1974) examined this in an informal study using himself as a subject, and tried to remember well-known expressions such as "four score and seven years ago, " "To be or not to be, that is the question," and "All's fair in love and war." He concluded that "lists of three such phrases were all I could recall with reliability, although I could sometimes retain four." Of course, the number of words and syllables contained in these phrases was much larger. Elsewhere in the article, for example, it was noted that 7 one-syllable words could be recalled. The present theoretical assumption is that, in the recall of phrases, each phrase served as a previously learned chunk and also was too long to allow effective rehearsal; thus, by aiming the focus of attention at the phrase level, four such phrases could be recalled despite their inclusion of many more units on a sub-chunk level. In the recall of isolated words, in contrast, given that each word was much shorter than a phrase, it was presumably possible to use rehearsal to reactivate memory (and possibly to form new chunks larger than a single word) and therefore to increase the number of words recalled above what would be expected if each word were a separate chunk. This reasoning is supported by the fact that about 4 unconnected spoken words can be recalled when rehearsal is blocked, as shown in Table 2.
Jones, Farrand, Stuart, and Morris (1995) carried out an experiment that reveals a capacity limit, though that was not the purpose of the experiment. On each trial, a series of dots was presented one at a time at different spatial locations on the computer screen. After a variable test delay, the response screen included all of the dots and the task was to point to them in the serial order in which they had been presented. There was very little loss of information over retention intervals of up to 30 s. The authors suggested that this stability of performance across test delays indicates that some sort of "rehearsal" process was used. I would suggest that the so-called rehearsal process used here does not contaminate the estimate of storage because it is not a true rehearsal process. Instead, it may be a process in which some of the items, linked to serial position or order, are held in the capacity-limited store. Each list presented by Jones et al. included 4, 7, or 10 dots. It can be estimated from their paper (Jones et al., Fig. 2, p. 1011) that these three list lengths led to means of 3.5, 3.8, and 3.2 items recalled in a trial, respectively. These estimates were obtained by calculating the mean proportion correct across serial positions and multiplying it by the number of serial positions.
Several studies of the memory for unrehearsable material produce estimates lower than 3.0. Glanzer and Razel (1974) examined the free recall of proverbs and estimated the short-term storage capacity using the method developed by Waugh and Norman (1965), based on the recency effect. The estimate was 2.0 proverbs in short-term storage on the average. Glanzer and Razel also estimated the contents of short-term storage for 32 different free recall experiments, and found a modal value of 2.0 - 2.4 items in storage, very comparable to what they found for the proverbs. However, there is a potential problem with the Waugh and Norman (1965) method of estimating the contents of short-term storage. They assumed that the most recent items are recalled from either of two sources: short-term storage or long-term storage. The estimate of short-term storage is obtained by taking the list-medial performance level to reflect long-term memory and assuming that the recency effect occurs because of this same memory plus the additional contribution of short-term memory. This assumption is problematic, though, if the items in the recency positions are not memorized in the same way but are more often recalled only with the short-term store and not with the same contribution of long-term storage that is found for the earlier list items. This possibility is strengthened by the existence of negative recency effects in the final free recall of lists that previously had been seen in immediate recall (Craik, Gardiner, & Watkins, 1970). Glanzer and Razel consequently may have overcorrected for the contribution of long-term memory in the recency positions.
Another low estimate was obtained for unrehearsable material by Zhang and Simon (1985) using Chinese. In their Experiment 1, the mean number of items recalled was 2.71 when the items were radicals without familiar pronounceable names, and 6.38 (like the usual English memory span) when the items were characters with pronounceable, rehearsable names, within which radicals were embedded. A lower estimate for unrehearsable items is to be expected. However, the fact that it was lower than 3 would not be expected if, as the authors asserted, there are over 200 such radicals and "educated Chinese people can recognize every radical" (p. 194), making each radical a single visual chunk. It seems possible that there are visual similarities among three or more radicals that tend to make them interfere with one another in memory when radicals are presented in a meaningless series, preventing them from serving as independent chunks. Although this analysis is speculative, the basis of the discrepancy between these few estimates below 3.0 and the estimates obtained in the many other experiments taken to reflect a capacity limit (in the 3 - 5 chunk range) is an important area for future research.
3.3. Capacity limits estimated with performance discontinuities. Although subjects in some procedures may be able to perform when there are more than 4 items, the function describing the quality or speed of performance sometimes shows a discontinuity when one reaches about 4 items (e.g., a much longer reaction time cost for each additional item after the fourth item). Presumably, in these circumstances, some optional processing mechanism must be used to supplement the capacity-limited store only if the stimuli exceed the capacity. This can occur in several ways as shown below.
3.3.1. Errorless performance in immediate recall. Broadbent (1975) noted that we usually measure span as the number of items that can be recalled on 50% of the trials. However, he cites evidence that the number of items that can be recalled reliably, with a very high accuracy, is about 3 or 4 and is much more resistant to modifications based on the nature of the items (Cardozo & Leopold, 1963; see also Atkinson & Shiffrin, 1968). That is, there is a flat performance function across list lengths until 3 or 4 items. It stands to reason that when items beyond 4 are remembered, it is through the use of supplementary mnemonic strategies (such as rehearsal and chunking), not because of the basic storage capacity.
3.3.2. Enumeration reaction time. The ability to apprehend a small number of items at one time in the conscious mind can be distinguished from the need to attend to items individually when a larger number of such items are presented. This point is one of the earliest to be noted in psychological commentaries on the limitations in capacity. Hamilton (1859) treated this topic at length and noted (Vol. 1, p. 254) that two philosophers decided that six items could be apprehended at once, whereas at least one other (Abraham Tucker) decided that four items could be apprehended. He went on to comment: "The opinion [of six] appears to me correct. You can easily make the experiment for yourselves, but you must be aware of grouping the objects into classes. If you throw a handful of marbles on the floor, you will find it difficult to view at once more than six, or seven at most, without confusion; but if you group them into twos, or threes, or fives, you can comprehend as many groups as you can units; because the mind considers these groups only as units, -it views them as wholes, and throws their parts out of consideration. You may perform the experiment also by an act of imagination." When the experiment actually was conducted, however, it showed that Hamilton's estimate was a bit high. Many studies have shown that the time needed to count a cluster of dots or other such small items rises very slowly as the number of items increases from 1 to 4, and rises at a much more rapid rate after that. Jevons (1871) was probably the first actual study, noting that Hamilton's conjecture was "one of the very few points in psychology which can, as far as we yet see, be submitted to experiment." He picked up handfuls of beans and threw them into a box, glancing at them briefly and estimating their number, which was then counted for comparison. After over a thousand trials, he found that numbers up to 4 could be estimated perfectly, and up to 5 with very few errors.
Kaufman, Lord, Reese, and Volkmann (1949) used the verb "subitize" to describe the way in which a few items apparently can be apprehended and enumerated in a very rapid fashion (as if these items enter the focus of attention at the same time). In contrast, when there are more items, the reaction time or the time necessary for accurate counting increases much more steeply as the number of items increases (as if these items must enter the focus of attention to be counted piecemeal, not all at once). Mandler and Shebo (1982) described the history of the subitizing literature. As they note, subitizing has been observed via two main procedures: one in which the duration of an array is limited and the dependent measure is the proportion of errors in estimating the number of items in the array, and another method in which the array stays on and the primary dependent measure is the reaction time to respond with the correct number. The results from the first of these methods seem particularly clear. For example, in results reported by Mandler and Shebo (1982, p. 8), the proportion of errors was near zero for arrays of 1-4 items (or for 1-3 items with a presentation duration as short as 200 msec) and increased steeply after that, at a rate of about 15% per additional item until nearly 100% error was reached with an array size of 11. The reaction time increased slowly with array sizes of 1-3 and more steeply for array sizes of 5-8. After that it leveled off (whereas it continued to increase at the same rate, for much higher array sizes, in procedures in which the array stayed on and the dependent measure was the time to produce the number). The average response was identical to the correct response for array sizes of 1-8, with an increasing degree of underestimation as array size increased from 9 to 20. From the present viewpoint, it would appear that 3 or 4 items were subitized initially and about 3 or 4 more could be added to the subitized amount without losing track of which items had been counted.
Alternative hypotheses about enumeration and related processes must be considered. Trick and Pylyshyn (1994) put forth a theory of subitizing suggesting that it is capacity-limited (hence the limit to 4 items), but still not attention-demanding, and that it takes place at a point in processing intermediate between unlimited-capacity automatic processes and serial or one-at-a-time attentive processes. It was called the FINST (finger of instantiation) theory in that there are a limited number of "fingers" of instantiation that can be used to define individual items in the visual field. This theory is specific to vision, and it was contrasted with a working memory theory in which subitizing is said to occur because of a limit in the number of temporary memory slots.
The evidence used by Trick and Pylyshyn (1994a) to distinguish between the theories is open to question. First, it was shown that items could be subitized only if they were organized in a way that made them "pop out" of the surroundings (the evidence of Trick & Pylyshyn, 1993). Certainly, this suggests that there is a pre-attentive stage of item individuation, but perhaps the subitization occurs only afterward, contingent not only on this rapid item individuation as Trick and Pylyshyn said, but contingent also on the availability of slots. One reason to make this distinction is that the phenomenon of popout clearly is not limited to four items; it obviously occurs for much larger numbers of items. For example, when one looks inside a carton of eggs, all of the eggs appear to pop out against the surrounding carton. It is the inclusion of individuated items in the enumeration routine that is limited to about 4. Another type of evidence used by Trick and Pylyshyn (1994a) was that there was said to be no effect of a memory load on subitization, unlike counting. Logie and Baddeley (1987) were the main authors cited in this regard, though subitization was not the focus of their study. Logie and Baddeley did find that two distractor tasks (articulatory suppression from repetition of the word "the," and tapping) had little effect in the subitizing range, whereas articulatory suppression had an effect in the counting range. However, these tasks can be carried out relatively automatically and would not be expected to require much working memory capacity (Baddeley, 1986). For example, unlike counting backward as a distractor task, which causes severe forgetting of a consonant trigram over an 18-s distractor-filled period (Peterson & Peterson, 1959), articulatory suppression causes almost no loss over a similar time period (Vallar & Baddeley, 1982). Interference with articulatory processing can explain why articulatory suppression interfered with counting, for items over 4 in the array task and also for every list length within another task that involved enumeration of sequential events rather than simultaneous spatial arrays. The data of Logie and Baddeley thus do seem to support the distinction between subitizing and counting, but they do not necessarily support the FINST theory over the working memory limitation theory of subitizing.
Another type of evidence (from Trick & Pylyshyn, 1994b) involved a cue validity paradigm (a variation of the procedure developed by Posner, Snyder, & Davidson, 1980). On each trial in most of the experiments, two rectangles appeared, and dots were to appear in only one rectangle. The task was to count the dots. Sometimes, there would be a cue (an arrow pointing to one rectangle or a flashing rectangle) to indicate slightly in advance which rectangle probably would contain the dots. The cue was valid (giving correct information) on 80% of the cued trials and invalid (giving incorrect information) on 20% of the cued trials. On other trials, no informative cue was given. The validity of the cue affected performance in the counting range more than in the subitizing range, leading Trick and Pylyshyn (1994a) to view the results as supportive of the FINST theory. However, there was still some effect of cue validity in the subitizing range, so the result is less than definitive in comparing the FINST and working memory accounts of subitizing.
Atkinson, Campbell, and Francis (1976) and then Simon and Vaishnavi (1996) investigated enumeration within afterimages so that subjects would be unable to shift their gaze in a serial fashion using eye movements. Both studies found that the subitizing limit remained at 4 items, with errors in enumeration only above that number, even though subjects had a long time to view each afterimage. Therefore, it seems that a focal attention strategy involving eye movements is important for visual enumeration of over 4 items, but not at or below 4 items, the average number that subjects may be able to hold in the limited-capacity store at one time.
3.3.3. Multi-object tracking. Another, more recent line of research involves "multi-object tracking" of dots or small objects that move around on the computer screen (Pylyshyn & Storm, 1988; Yantis, 1992; for a recent review see Pylyshyn, Burkell, et al., 1994). In the basic procedure, before the objects move, some of them flash several times and then cease flashing. After that all of them wander randomly on the screen and, when they stop, the subject is to report which dots had been flashing. The flavor of the results is described well by Yantis (1992, p. 307): "Performance deteriorated as the number of elements to be tracked increased from 3 to 5 [out of 10 on the screen]; tracking three elements was viewed by most subjects as relatively easy, although not effortless, while tracking 5 of 10 elements was universally judged to be difficult if not impossible by some subjects." As in subitizing, one could use either FINST or working memory theories to account for this type of finding.
3.3.4. Proactive interference in short-term memory. One can observe proactive interference (PI) in retrieval only if there are more than 4 items in a list to be retained (Halford et al., 1988). This presumably occurs because 4 or fewer items are, in a sense, already retrieved; they reside in a limited-capacity store, eliminating the retrieval step in which PI arises. Halford et al. demonstrated this storage capacity limit in a novel and elegant manner. They used variant of Sternberg's (1966) memory search task, in which the subject receives a list of items and then a probe item and must indicate as quickly as possible whether the probe appeared in the list. In their version of the task, modeled after Wickens, Moody, and Dow (1981), lists came in sets of three, all of which were similar in semantic category (Experiment 1) or rhyme category (Experiment 2). Thus, the first trial in each set of three was a low-PI trial, whereas the last trial in the set was a high-PI trial. Experiment 1 showed that with lists of 10 items, there were PI effects. With a list length of 4, there was no PI. Experiment 2 showed that PI occurred for lists of 6 or more items, but not lists of 4 items. Presumably, the items within a list of 4 did not have to be retrieved because they all could be present within a capacity-limited store at the same time. Also consistent with this sort of interpretation, in 8- to 9-year-old children PI was observed with 4 items, but not 2 items in a list. The magnitude of growth of a capacity limit with age in childhood matches what was observed by Cowan et al. (1999) with a very different procedure (see Figure 2).
In the Halford et al. (1988) study, it was the length of the target list that was focused upon. We can learn more by examining also the effect of variations in the length of the list causing PI. Wickelgren's (1966) subjects copied a list of PI letters, a single letter to be recalled, and then a list of retroactive interference (RI) letters. The subject was to recall only the target letter. There were always 8 letters in one of the interference sets (the PI set for some subjects, the RI set for others), whereas the other interfering set could contain 0, 4, 8, or 16 letters. There was a large effect of the number of RI letters, with substantial differences between any two RI list lengths. In contrast, when it was the PI set that varied in length, there was a difference between 0 and 4 PI letters but very little effect of additional PI letters beyond 4. Wickelgren suggested that PI and RI both generate associative interference, whereas RI additionally generates another source of forgetting (either decay or storage interference). Thus, associative interference would have been limited primarily to the 4 closest interfering items on either side of the target.
A mechanism of PI in these situations can be suggested. It seems likely that excellent, PI-resistant recall occurs when the active contents of the limited-capacity store are to be recalled. When the desired information is no longer active, the long-term memory record of the correct former state of the limited-capacity store can be used as a cue to the recall of the desired item(s). If several former limited-capacity states were similar in content, it may be difficult to select the right one. Moreover, if the limited-capacity store serves as a workspace in which items become associated with one another (Baars, 1988; Cowan, 1995), then it might be difficult to select the correct item from among several present in the limited-capacity store simultaneously. The PI results described above could then be interpreted as follows. For studies in Halford et al. (1988), target lists of more than 4 items could not be held entirely within limited-capacity storage, so that a former state of the store had to be reconstituted. This could cause PI because some of the target items may have shared a former limited-capacity state with nearby items from a prior list, or because some of the other former limited-capacity states would have contained items resembling the correct item. For subjects in Wickelgren's (1966) study who received a variable number of PI letters, the target item would have been removed from the limited-capacity store by the presentation of 8 following RI letters. Therefore, at the time of recall, the subject would have had to identify the former state of the limited-capacity store that contained the single target letter. This same former state may also have included several of the adjacent letters, which could become confused with the target letter. Only 3 or so letters adjacent to the target letter usually would have been in the limited-capacity store at the same time as the target letter, and thus only those letters would contribute much to associative interference. In a broader context, this analysis may be one instance of a cue-overload theory of PI (cf. Glenberg & Swanson, 1996; Raaijmaker & Shiffrin, 1981; Tehan & Humphreys, 1996; O.C. Watkins & M.J. Watkins, 1975) asserting that recall is better when fewer test items are associated with the cue used to recall the required information.
3.4. Capacity limits estimated with indirect effects. So far we have discussed effects of the number of stimulus items on a performance measure directly related to the subject's task, in which recall of items in the focus of attention is required. It is also possible to observe effects that are related to the subject's task only indirectly by deriving a theoretical estimate of capacity from the presumed role of the focus of attention in processing.
3.4.1. Chunk size in immediate recall. The "magical number 4" lurks in the background of the seminal article by Miller (1956) on the magical number 7 + 2, which emphasized the process of grouping elements together to form larger meaningful units or "chunks." The arrangement of telephone numbers with groups of 3 and then 4 digits would not appear to be accidental, but rather an indication of how many elements can be comfortably held in the focus of attention at one time to allow the formation of a new chunk in long-term memory (Baars, 1988; Cowan, 1995). Several investigators have shown that short-term memory performance is best when items are grouped into sublists of no more than 3 or 4 (Broadbent, 1975; Ryan, 1969; Wickelgren, 1964).
The grouping limit even seems to apply for subjects who have learned how to repeat back strings of 80 or more digits (Ericsson, Chase, & Faloon, 1980; Ericsson, 1985). These subjects did so by learning to form meaningful chunks out of small groups of digits, and then learning to group the chunks together to form "supergroups." At both the group and the supergroup levels, the capacity limit seems to apply, as described by Ericsson et al. (1980, p. 1182) for their first subject who increased his digit span greatly: "After all of this practice, can we conclude that S.F. increased his short-term memory capacity? There are several reasons to think not...The size of S.F.'s groups were almost always 3 and 4 digits, and he never generated a mnemonic association for more than 5 digits...He generally used three groups in his supergroups and, after some initial difficulty with five groups, never allowed more than four groups in a supergroup." Ericsson (1985) reviewed details of the hierarchical grouping structure in the increased-digit-span subjects and he reviewed other studies of memory experts, which also revealed a similar grouping limit of 3-5 items. This limit to the grouping process would make sense if the items or groups to be further grouped together must reside in a common, central workspace so that they can
 2015-09-06
2015-09-06 603
603