Расчет напряжений и деформаций в диске
Предположим, что выполняются следующие условия:
- диск (рис.1) достаточно тонкий, поэтому распределение напряжений по толщине 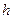 можно принять равномерным. Напряженное состояние в диске двухосное, характеризуется радиальным напряжением
можно принять равномерным. Напряженное состояние в диске двухосное, характеризуется радиальным напряжением 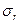 и окружным напряжением
и окружным напряжением 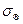 ;
;
- температурное поле диска – плоское осесимметричное; температура диска 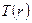 зависит только от радиуса
зависит только от радиуса 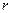 и постоянна по толщине диска;
и постоянна по толщине диска;
- величины 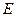 (модуль упругости) и
(модуль упругости) и 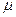 (отношение размеров трещины и детали) постоянные для всего диска, их зависимостью от температуры пренебрегаем.
(отношение размеров трещины и детали) постоянные для всего диска, их зависимостью от температуры пренебрегаем.
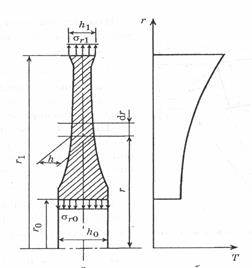
Рис.1 Тонкий диск (профиль и распределение температуры)
Диск равномерно вращается с угловой скоростью 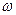 ; на внешней цилиндрической поверхности (при
; на внешней цилиндрической поверхности (при 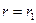 ) действуют равномерно распределенные по толщине напряжения
) действуют равномерно распределенные по толщине напряжения 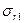 , вызываемые центробежными силами обода и рабочих лопаток,
, вызываемые центробежными силами обода и рабочих лопаток,
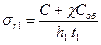 , (1)
, (1)
где 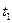 - шаг лопаток по окружности радиуса
- шаг лопаток по окружности радиуса 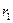 ;
; 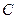 - центробежная сила одной лопатки;
- центробежная сила одной лопатки; 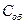 - центробежная сила обода диска, отнесенная к шагу
- центробежная сила обода диска, отнесенная к шагу 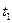 (см. рис. 2), где сечение
(см. рис. 2), где сечение 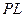 соответствует радиусу
соответствует радиусу 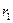 (на рис. 3);
(на рис. 3); 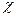 - поправочный коэффициент
- поправочный коэффициент 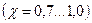 .
.
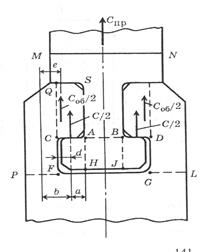
Рис.2 Схема Т-образного замкового соединения
При названных условиях необходимо определить распределение напряжений 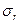 и
и 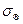 по радиусу диска.
по радиусу диска.
Для решения задачи следует составить уравнение равновесия и совместности деформаций и выбрать закон деформирования (закон Гука).
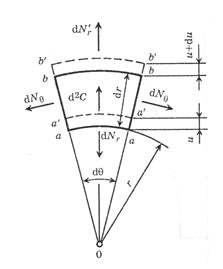
Рис.3 Схема нагружения элемента диска
На элемент диска, выделенный двумя цилиндрическими сечениями на радиусах 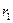 и
и 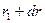 и двумя меридиональными плоскостями с углом
и двумя меридиональными плоскостями с углом 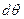 между ними (рис.3), действуют поверхностные силы:
между ними (рис.3), действуют поверхностные силы:
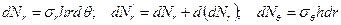 ,
,
обусловленные напряжениями 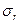 и
и 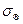 , а также объемная сила (центробежная сила инерции)
, а также объемная сила (центробежная сила инерции) 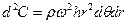 . Проектируя все названные силы на направление радиуса, проходящего через центр элемента, получаем
. Проектируя все названные силы на направление радиуса, проходящего через центр элемента, получаем
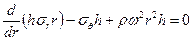 . (2)
. (2)
Из курса сопротивления материалов известны соотношения
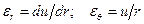 , (3)
, (3)
где 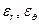 - радиальное и окружное относительное удлинения (деформации) в диске;
- радиальное и окружное относительное удлинения (деформации) в диске; 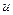 - радиальное смещение на произвольном радиусе (рис.2).
- радиальное смещение на произвольном радиусе (рис.2).
Исключая смещение 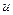 из первого соотношения (3) при помощи второго соотношения, получаем уравнение совмесности деформаций
из первого соотношения (3) при помощи второго соотношения, получаем уравнение совмесности деформаций
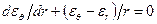 . (4)
. (4)
Уравнение равновесия (2) и совмесности (4) не зависят от закона деформирования материала и одинаково применимы как к упругому диску, так и в условиях упругопластических деформаций или ползучести.
Закон Гука при двухосном напряженном состоянии получим из зависимости (5), предположив, что 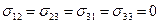 .
.
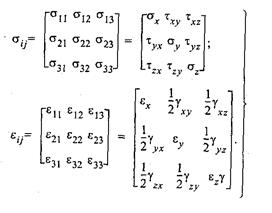 (5)
(5)
Обозначим 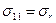 ;
; 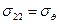 ;
; 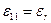 ;
; 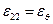 ;
; 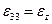 .
.
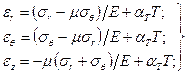 , (6)
, (6)
где 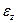 - деформация вдоль оси диска.
- деформация вдоль оси диска.
Подставив деформации 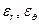 из системы (6) в уравнение (4), получим уравнение совместности в виде
из системы (6) в уравнение (4), получим уравнение совместности в виде
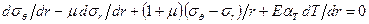 . (7)
. (7)
Система уравнений (2) и (7) содержит две неизвестные величины 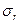 и
и 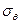 .
.
Решение системы позволит определить искомые напряжения, которые должны удовлетворить граничным условиям:
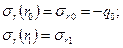 , (8)
, (8)
где 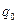 - давление посадки диска на валу.
- давление посадки диска на валу.
Таким образом, на границах (на расточке диска и периферии радиальное напряжение должно иметь заданные значения.
В общем случае, когда диск имеет переменную толщину 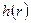 , необходимо применение численных методов для решения полученной системы уравнений. Рассмотрим частный случай диска постоянной толщины, для которого существует простое аналитическое решение.
, необходимо применение численных методов для решения полученной системы уравнений. Рассмотрим частный случай диска постоянной толщины, для которого существует простое аналитическое решение.
Диск постоянной толщины
Полагая 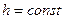 , из (2) имеем
, из (2) имеем
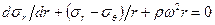 . (9)
. (9)
Для получения общего решения уравнений (9) и (7) умножим уравнение (9) на 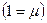 и сложим с уравнением (7).
и сложим с уравнением (7).
Тогда
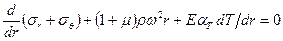 . (10)
. (10)
Интегрируем последнее уравнение
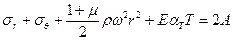 , (11)
, (11)
где 2 А – постоянная интегрирования.
Умножим все члены уравнения (10) на 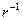 и сложим левые и правые части (9) для исключения
и сложим левые и правые части (9) для исключения 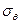 . После преобразования получим уравнение относительно одной переменной
. После преобразования получим уравнение относительно одной переменной 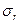
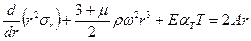 .
.
В результате интегрирования последнего уравнения получаем
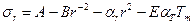 ; (12)
; (12)
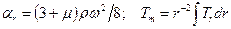 , (13)
, (13)
где В – вторая постоянная интегрирования.
Теперь из уравнения (10) учитывая (11), находим и 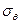 :
:
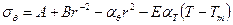 ; (14)
; (14)
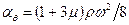 . (15)
. (15)
Формулы (12) и (14) представляют собой общее решение для напряжений в диске постоянной толщины. Постоянные интегрирования А и В должны быть найдены из граничных условий (8)на периферии и на расточке диска.
Рассмотрим отдельно динамические и температурные напряжения. Вследствие линейности задачи суммарные напряжения в диске, очевидно, равны алгебраической сумме динамических и температурных напряжений.
Динамические напряжения в диске постоянной толщины без центрального отверстия 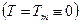
Граничные условия
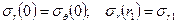 . (16)
. (16)
Первое граничное условие из (16) означает, что в центре диска без центрального отверстия радиальное и окружное напряжения совпадают вследствие того, что исчезает различие между окружным и радиальным направлениями.
Применяя условия (16) к решению (12) (при 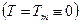 , получаем
, получаем
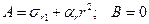 .
.
Распределение напряжений по полотну диска теперь представляется формулами
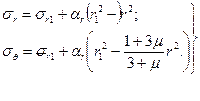 (17)
(17)
На рис. 4 показаны эпюры напряжений, соответствующие рассмотренному случаю.
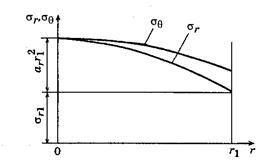
Рис. 4 распределение напряжений в сплошном диске постоянной толщины
 2015-10-16
2015-10-16 1020
1020







