III. Метод Гаусса

Метод является универсальным, т.к. он позволяет решать системы линейных алгебраических уравнений с матрицами любой размерности и квадратными матрицами с определителем, равным нулю.

Метод Гаусса состоит в том, что производятся последовательные преобразования исходной системы уравнений в эквивалентную систему до тех пор, пока решение последней не станет очевидным или не станет очевидной неразрешимость системы.

Этот процесс осуществляется с помощью элементарных преобразований система линейных алгебраических уравнений, аналогичных элементарным преобразованиям матрицы до получения матриц эквивалентной системы ступенчатого вида.

Элементарные преобразования системы уравнений:

1.Перестановка любых двух уравнений.

2. Умножение обеих частей уравнения на одно и то же число, не равное нулю.

3. Прибавление к обеим частям одного уравнения системы соответствующих частей другого, умноженных на одно и то же число.

4. Вычеркивание уравнение вида 0·х₁+0·х₂+…+0·х_n=0 как не несущего ни какой информации относительно решений системы.

Пример: Рассмотрим решение предыдущей системы методом Гаусса:

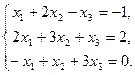
Решение: Можно вместо преобразования системы осуществлять преобразование её расширенной матрицы.

А|В= .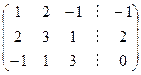

Метод Гаусса включает два процесса, называющиеся прямым и обратным ходом соответственно.

На первом шаге прямого хода назовем разрешающий элемент —элемент a₁₁ расширенной матрицы, первую строку— разрешающей строкой, а первый столбец— разрешающим столбцом.

Если этот элемент равен нулю, то поменяем местами уравнения так, что бы этот элемент ни был равен нулю.

Цель прямого хода —преобразовать расширенную матрицу данной системы в матрицу ступенчатого вида.

На каждом шаге прямого хода следует руководствоваться следующими тремя правилами.

1). Элементы разрешающей строки остаются неизменными на данном и всех последующих шагах.

2).Элементы разрешающего столбца, расположенные ниже разрешающего элемента, обращаются в нули и остаются нулями до конца прямого хода.

3). Остальные элементы пересчитываются по правилу прямоугольника.

Проводим первый шаг прямого хода для исходной матрицы.

.

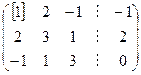
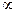
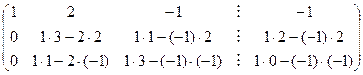
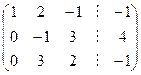На втором шаге прямого хода метода Гаусса за разрешающий элемент принимаем элемент, стоящий во второй строке и во втором столбце полученной матрицы. Если он равен нулю, то производим перестановку строк матрицы.

Далее по вышеуказанным правилам.

.

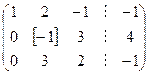
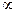
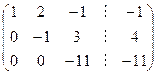Получим матрицу ступенчатого вида. На основе этой матрицы выпишем систему уравнений, эквивалентную исходной системе:

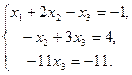
Проводим обратный ход. Из третьего уравнения находим х ₃; подставляем его значение во второе уравнение и находим х ₂ и т. д.

x₃= 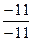=1;

-x₂+3·1=4; -x₂=1; x₂=-1;

x₁+2·(-1)-1=-1; x₁-3=-1; x₁=2.

Обратный ход можно также проводить аналогично прямому, при этом пользуясь теми же правилами. Во втором правиле в нули обращаются элементы разрешающего столбца, расположенные не ниже, а выше разрешающего элемента.

За разрешающий элемент на первом шаге обратного хода принимается крайний элемент последней строки.

Если разрешающий элемент не равен единице, то целесообразно разрешающую строку разделить на разрешающий элемент, что является элементарным преобразованием и не разрушает равносильности системы.

Проведем обратный ход:

.

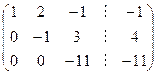
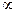
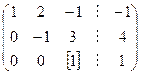
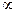
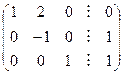
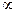
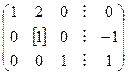
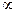
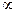
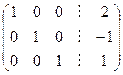Получим расширенную матрицу системы, эквивалентной исходной, из которой элементарно выписывается решение:

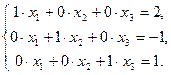Откуда x₁=2; x₂=-1; x₃=1.

Можно объединить прямой и обратный ходы метода Гаусса в один ход. При этом в качестве разрешающего элемента выбирается любой ненулевой элемент матрицы системы, но на каждом последующем шаге в другой строке и в другом столбце.

В этом случае обнуляются все элементы разрешающего столбца, кроме разрешающего элемента. Пересчету по правилу прямоугольника подлежат все элементы расширенной матрицы, не принадлежащие разрешающей строке и разрешаемому столбцу. Такой алгоритм метода Гаусса часто называют методом Жордана.

5. Рекомендуемое содержание отчета (для студента).

1. Название лабораторной работы.

2. Цель и задачи исследований.

3. Электронно-вычислительные средства для расчетов.

4. Журнал (тетрадь) исследований (вычислений) с обработкой полученных данных в виде таблиц, графиков (по требованию).

5. Выводы.

6. Анализ и защита лабораторной работы производится по результатам представленного студенческой группой отчета (перечень сделанного, рекомендации, ответы на рассмотренные в процессе выполнения контрольные вопросы).

Преподаватель оценивает знание каждого студента.

Литература