Пример 1.1 Классический метод Гаусса

Содержание

Содержание.. 1

1. Решение систем линейных алгебраических уравнений.. 2

1.1. Классический метод Гаусса.. 2

1.2. Метод Гаусса с выбором главного элемента.. 6

2. Метод Ньютона для СНАУ.. 8

2.1. Вариант 1.. 8

2.2. Вариант 2.. 9

3. Аппроксимация данных методом наименьших квадратов.. 12

3.1. Аппроксимация данных методом наименьших квадратов.. 12

3.2. Аппроксимация данных с другими нормами.. 13

3.3. Аппроксимация данных многочленом заданной степени.. 14

4. Решение систем дифференциальных уравнений.. 19

4.1. Метод Эйлера.. 19

4.2. Методы Рунге-Кутта.. 19

1. Решение систем линейных алгебраических уравнений

Классический метод Гаусса (его называют также простым методом Гаусса, методом последовательного исключения неизвестных) применим при условии, что все ведущие коэффициенты (диагональные) отличны от нуля! Решить систему методом Гаусса можно примерно за 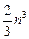арифметических действий. Для сравнения отметим, что решить подобную систему по правилу Крамера можно лишь за 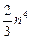действий. Таким образом, формула Крамера удобна для теоретического исследования свойств решения, но очень невыгодна для его численного нахождения.

Пусть необходимо решить СЛАУ (1.2) и пусть 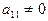(ведущий элемент).

Метод Гаусса или метод последовательного исключения неизвестных основан на приведении матрицы коэффициентов 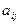к верхнему треугольному виду. При этом алгоритм решения системы (1.2) следующий.

1. С помощью двух циклов с управляющими переменным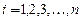и и 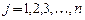организуем ввод коэффициентов 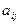и .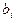

2. Проводим прямой ход исключения переменных путём преобразования коэффициентов по формулам:

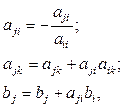
где , .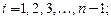

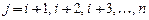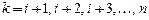В конце этих преобразований получим

.

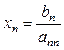3. Организуем обратный ход (последовательное нахождение корней 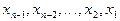), проводя вычисления по формулам:

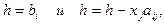
где .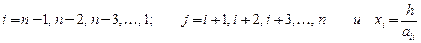

В результате формируется массив неизвестных

.

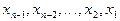{Прямой ход исключения переменных}

For i:= 1 to N-1 do

For j:= i+1 to N do