Три некомпланарных вектора  ,
,  и
и 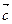 , взяты в указанном порядке, образуют правую (левую) тройку, если при наблюдении с конца вектора
, взяты в указанном порядке, образуют правую (левую) тройку, если при наблюдении с конца вектора 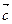 кратчайший поворот от первого вектора
кратчайший поворот от первого вектора  ко второму вектору
ко второму вектору  совершается против движения часовой стрелки (по часовой стрелке) (рис.6.1).
совершается против движения часовой стрелки (по часовой стрелке) (рис.6.1).
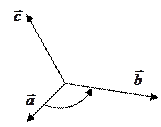 правая тройка
правая тройка
| 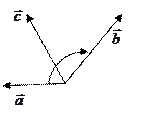 левая тройка
левая тройка
|
Рис.6.1.
Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор 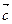 , определяемый следующими условиями:
, определяемый следующими условиями:
1) вектор 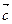 перпендикулярен каждому из векторов
перпендикулярен каждому из векторов  и
и  , т.е.
, т.е. 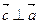 и
и 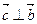 ;
;
2) длина вектора 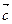 равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах  и
и  как на сторонах (рис.6.2), т.е.
как на сторонах (рис.6.2), т.е.
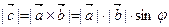 , где
, где 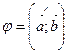 ; (6.1)
; (6.1)
3) векторы  ,
,  и
и 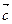 образуют правую тройку, т.е. тройка векторов
образуют правую тройку, т.е. тройка векторов  ,
,  и
и 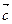 имеет ту же ориентацию, что и тройка единичных координатных векторов
имеет ту же ориентацию, что и тройка единичных координатных векторов 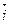 ,
, 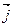 и
и 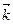 (рис.6.3).
(рис.6.3).
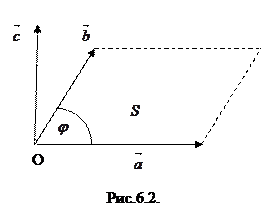
| 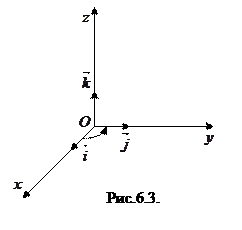
|
Векторное произведение векторов обозначается 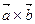 или
или 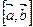 .
.
1) векторное произведение меняет знак при перестановке сомножителей:
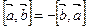 ;
;
2) векторное произведение обладает сочетательным свойством относительно скалярного множителя:
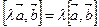 ;
;
3) векторное произведение обладает распределительным свойством:
|
|
|
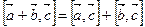 ;
;
Если векторы  и
и  заданы своими координатами
заданы своими координатами 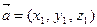 и
и 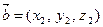 ,то
,то
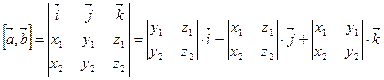 (6.2)
(6.2)
Формулы, применяемые при решении задач
1. Площадь параллелограмма и треугольника:
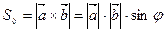 , (6.3)
, (6.3)
 . (6.4)
. (6.4)
2. Векторное произведение равно нулевому вектору, если два ненулевых вектора  и
и  коллинеарны:
коллинеарны:
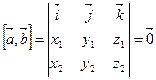
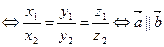 .
.
3. Момент силы. Пусть к точке 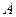 приложена сила
приложена сила 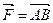 и
и 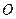 - некоторая точка пространства (рис. 6.4). Известно, что моментом силы
- некоторая точка пространства (рис. 6.4). Известно, что моментом силы 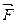 относительно точки
относительно точки 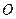 называется вектор
называется вектор 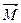 , который перпендикулярен плоскости, проходящей через точки
, который перпендикулярен плоскости, проходящей через точки 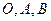 , численно равен произведению силы на «плечо»
, численно равен произведению силы на «плечо»
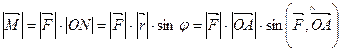
и образует правую тройку с векторами 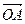 и
и 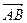 .
.
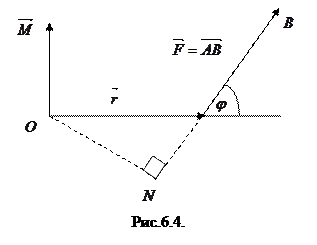
4. Скорость вращения. Скорость 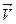 точки
точки 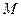 твердого тела, вращающегося с угловой скоростью
твердого тела, вращающегося с угловой скоростью 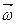 вокруг неподвижной оси, определяется формулой Эйлера
вокруг неподвижной оси, определяется формулой Эйлера 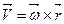 , где
, где 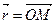 ,
, 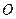 - некоторая неподвижная точка оси (рис.6.5).
- некоторая неподвижная точка оси (рис.6.5).
|  
|
Задача 6.1. Даны два вектора  и
и  , для которых
, для которых 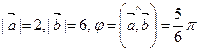 . Найти
. Найти 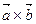 и
и 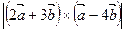 .
.
Решение. По формуле (6.1) находим 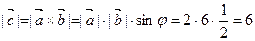 . Согласно свойствам векторного произведения получаем:
. Согласно свойствам векторного произведения получаем: 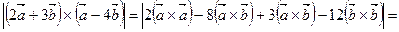
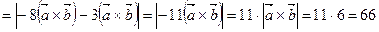 .
.
Задача 6.2. Найти площадь треугольника, вершины которого равны 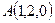 ,
, 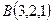 ,
, 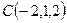 .
.
Решение. Согласно формуле (6.4) площадь треугольника 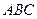 равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах 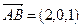 и
и 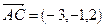 . Тогда
. Тогда
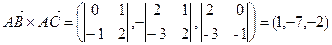 ,
,
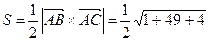 ,
, 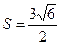 .
.
Задача 6.3. Дан треугольник с вершинами 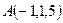 ,
, 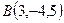 ,
, 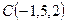 . Найтидлину высоты, проведенной из вершины
. Найтидлину высоты, проведенной из вершины 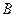 к стороне
к стороне 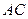 .
.
Решение. Согласно формул (6.3) и (6.4) площадь треугольника 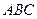 равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах 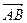 и
и 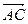 . Так как
. Так как 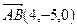 ,
, 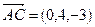 , то
, то 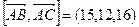 . Площадь параллелограмма
. Площадь параллелограмма
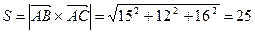 . Так как
. Так как 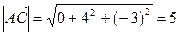 ,
, 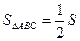 ,
, 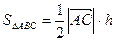 , то
, то  , откуда
, откуда 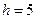 .
.
Задача 6.4. Сила 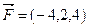 приложена в точке
приложена в точке 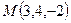 . Найти величину и направляющие косинусы момента этой силы относительно начала координат.
. Найти величину и направляющие косинусы момента этой силы относительно начала координат.
Решение. Если 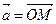 , то
, то 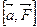 - момент силы
- момент силы 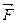 относительно точки
относительно точки 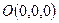 . Применяя формулу (6.2), получаем
. Применяя формулу (6.2), получаем 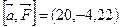 . Следовательно,
. Следовательно,
|
|
|
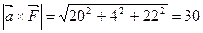 ,
, 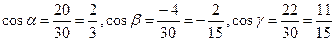 .
.
 2015-10-14
2015-10-14 922
922







