Смешанным произведением трех векторов  ,
,  и
и 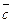 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 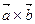 на вектор
на вектор 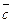 .
.
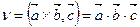 (7.1)
(7.1)
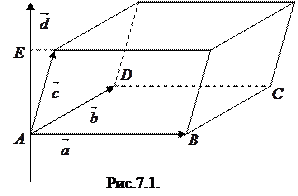 Смешанное произведение трех некомпланарных векторов
Смешанное произведение трех некомпланарных векторов  ,
,  ,
, 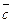 численно равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «+», если вектора
численно равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «+», если вектора  ,
,  ,
, 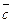 образуют правую тройку и со знаком «-с» если они образуют левую тройку (рис.7.1).
образуют правую тройку и со знаком «-с» если они образуют левую тройку (рис.7.1).
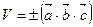 . (7.2)
. (7.2)
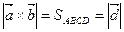 ,
,
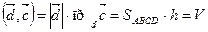 .
.
Смешанное произведение векторов  ,
,  ,
, 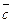 используется для вычисления объема треугольной пирамиды, построенной на этих векторах
используется для вычисления объема треугольной пирамиды, построенной на этих векторах 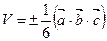 .
.
Свойства смешанного произведения векторов
1. Смешанное произведение не меняется при циклической перестановке векторов:
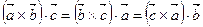 .
.
2. Смешанное произведение не меняется при перестановке знаков векторного и скалярного умножения: 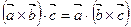 .
.
3. Смешанное произведение меняет знак на противоположный при перемене мест любых двух векторов-сомножителей: 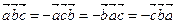 .
.
4. Смешанное произведение ненулевых векторов  ,
,  и
и 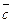 равно нулю, если они компланарны. Если векторы
равно нулю, если они компланарны. Если векторы 
 и
и 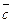 заданы своими координатами
заданы своими координатами 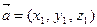 ,
, 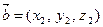 и
и 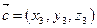 , то
, то
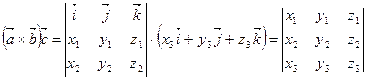 . (7.3)
. (7.3)
Задача 7.1. Вычислить 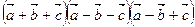 .
.
Решение. Используя свойства смешанного произведения векторов, получаем:
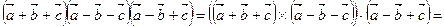
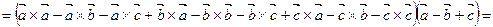
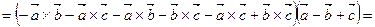
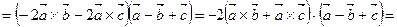
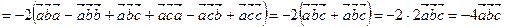 .
.
Задача 7.2. Доказать, что точки 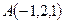 ,
, 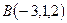 ,
, 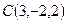 и
и 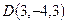 лежат в одной плоскости.
лежат в одной плоскости.
Решение. Рассмотрим три вектора 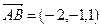 ,
, 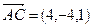 и
и 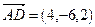 . По формуле (7.3) вычислим их смешанное произведение:
. По формуле (7.3) вычислим их смешанное произведение:
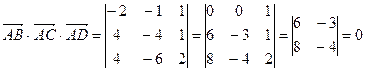 .
.
Так как 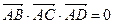 , то векторы
, то векторы 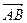 ,
, 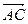 и
и 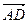 компланарны. Следовательно, точки
компланарны. Следовательно, точки 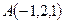 ,
, 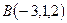 ,
, 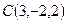 и
и 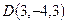 лежат в одной плоскости.
лежат в одной плоскости.
Задача 7.3. Вершинами пирамиды служат точки 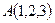 ,
, 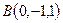 ,
, 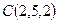 и
и 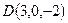 . Найти объем пирамиды.
. Найти объем пирамиды.
Решение. Вычислим координаты векторов 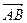 ,
, 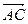 и
и 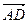 :
:
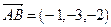 ,
, 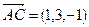 и
и 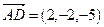 . Найдем значение смешанного произведения
. Найдем значение смешанного произведения
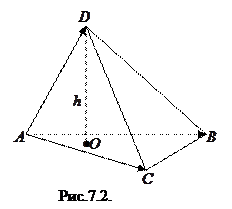
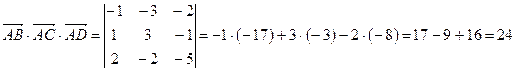 .
.
Согласно формуле 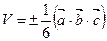 , получаем
, получаем 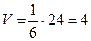 .
.
Задача 7.4. Даны вершины пирамиды 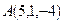 ,
, 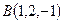 ,
, 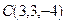 и
и 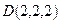 . Найти длину высоты, опущенной из вершины
. Найти длину высоты, опущенной из вершины 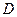 на грань
на грань 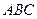 .
.
Решение. Так как 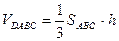 , то
, то 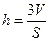 .
.
Согласно формуле 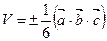 , где
, где 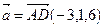 ,
, 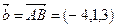 и
и 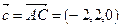 объем пирамиды:
объем пирамиды:
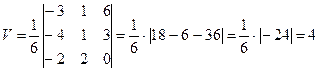 .
.
Находим площадь основания пирамиды 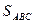 :
:
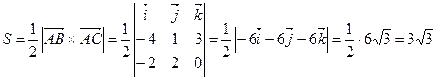 .
.
Следовательно, 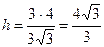 .
.
 2015-10-14
2015-10-14 593
593








