Вычисление производных функций.
Геометрический и физический смысл производной.
Производные высших порядков
1. Цель работы
Приобретение умений дифференцировать функции, заданные явно, неявно и параметрически, находить производные высших порядков, решать задачи на геометрический и физический смысл производной, в том числе и средствами программы MathCAD.
2. Содержание работы
1) Вычислите производные функций y = f (x) (табл. 1, задания А, Б, В). Решение оформите в тетради.
2) Вычислите производные функций, заданных неявно и параметрически (табл. 2). Решение оформите в тетради.
3) Составьте уравнения касательной и нормали к графику функции y = f (x) в точке с абсциссой х 0 (табл. 3). Решение оформите в тетради.
4) Вычислите вторые производные функций (табл. 1, задание Г и табл. 2, задание Б). Решение оформите в тетради.
5) Найдите скорость и ускорение в момент времени t 0 материальной точки, которая движется по закону S = S (t) (табл. 4). Решение оформите в тетради и сдайте на проверку.
6) Используя программу MathCAD, найдите первую и третью производные функции y = f (x) (табл. 5). Выполненное задание отчитайте преподавателю.
|
|
|
3. Общие сведения и примеры выполнения заданий
Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, называется производной функции y = f (x) в точке х и обозначается 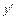 или
или 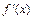 , т.е.
, т.е. 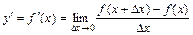 (рис. 1).
(рис. 1).
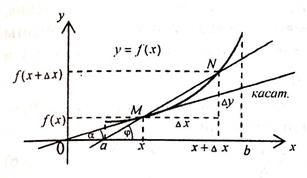
Рис. 1
Таблица производных
1) 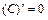 , где С – const. 8)
, где С – const. 8)  .
.
2) 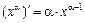 , где a – действительное число. 9)
, где a – действительное число. 9) 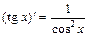 .
.
3)  , где a > 0, a ¹ 1. 10)
, где a > 0, a ¹ 1. 10) 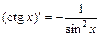 .
.
4) 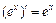 . 11)
. 11) 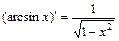 .
.
5) 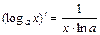 , где a >0, a ¹1. 12)
, где a >0, a ¹1. 12) 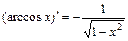 .
.
6) 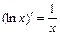 . 13)
. 13) 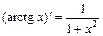 .
.
7) 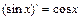 . 14)
. 14) 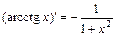 .
.
Правила дифференцирования
1) 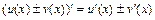 .
.
2) 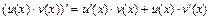 .
.
3)  , где C – const.
, где C – const.
4) 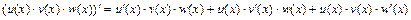 .
.
5) 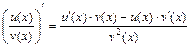 .
.
Пусть y = f (t), где t = j(x). Тогда производная сложной функции y = f (j(x)) находится по правилу:
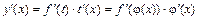 . (1)
. (1)
Если сложная функция образована суперпозицией более двух функций, то формулу (1) нужно применить соответствующее число раз.
Пример 1. Найдите производную функции:
а) 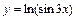 ; б)
; б) 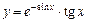 ; в)
; в) 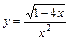 .
.
Решение. а) Используем формулу (1) и таблицу производных. Получим:
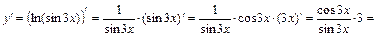
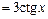 .
.
б) Используем правило дифференцирования произведения двух функций, формулу (1) и таблицу производных. Получим:

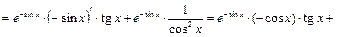
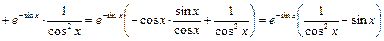 .
.
в) Используем правило дифференцирования частного, формулу (1) и таблицу производных. Получим:
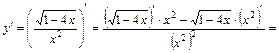
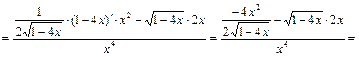
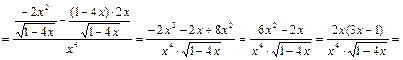
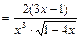 .
.
Ответ: а) 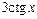 ; б)
; б)  ; в)
; в) 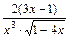 .
.
Если функция задана неявно, т. е. уравнением F (x; y) = 0, не разрешенным относительно y, то для нахождения производной 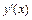 нужно найти производные от левой и правой части уравнения, считая, что y (х) есть сложная функция от х, и полученное после этого уравнение разрешить относительно искомой производной
нужно найти производные от левой и правой части уравнения, считая, что y (х) есть сложная функция от х, и полученное после этого уравнение разрешить относительно искомой производной 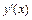 .
.
Пример 2. Найдите производную функции, заданную неявно:
а) x 2 + 3 xy – y 3 = cos y – 1, б) х 4 – ху + у 4 = 1.
Решение. а) Помня, что y есть сложная функция от x и, применяя правила дифференцирования суммы, произведения, а также таблицу производных, получим:
|
|
|
 ,
,
 ,
,
 ,
,
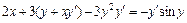 ,
,
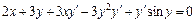 ,
,
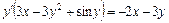 ,
,
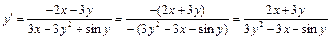 .
.
б) Рассуждая аналогично, получим:
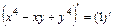 ,
,
 ,
,
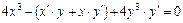 ,
,
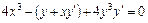 ,
,
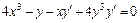 ,
,
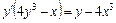 ,
,
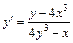 .
.
Ответ: а) 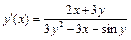 , б)
, б) 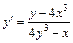 .
.
Если функция задана параметрически  где t – параметр, то производная
где t – параметр, то производная 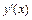 находится по формуле:
находится по формуле:
 . (2)
. (2)
Пример 3. Найдите производную функции 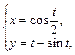 заданную параметрически.
заданную параметрически.
Решение. Вычисляя по формуле (2), используем правило дифференцирования разности, формулу (1) и таблицу производных. Получим:
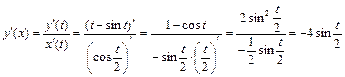 .
.
Указание. Преобразование 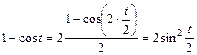 получено по формуле понижения степени:
получено по формуле понижения степени: 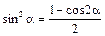 .
.
Ответ:  .
.
Предельное положение секущей, когда точки M и N совпадут, называется касательной к графику функции y = f (x) в точке М (рис. 1).
Производная 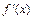 имеет геометрический смысл углового коэффициента касательной, проведенной к графику функции y = f (x) в точке М (x; f (x)). Если точка М имеет фиксированные координаты (x 0; f (x 0)), то
имеет геометрический смысл углового коэффициента касательной, проведенной к графику функции y = f (x) в точке М (x; f (x)). Если точка М имеет фиксированные координаты (x 0; f (x 0)), то 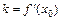 и уравнение касательной примет вид:
и уравнение касательной примет вид:
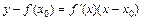 . (3)
. (3)
Прямая, проходящая через точку М (x 0; f (x 0)) перпендикулярно касательной, называется нормалью. Уравнение нормали имеет вид:
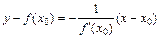 , (4)
, (4)
если  . При
. При 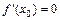 уравнение нормали имеет вид х = х 0.
уравнение нормали имеет вид х = х 0.
Пример 4. Составьте уравнения касательной и нормали к графику функции 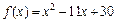 в точке с абсциссой х 0 = 3.
в точке с абсциссой х 0 = 3.
Решение. Найдем ординату точки х 0: 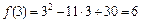 .
.
Т.к. 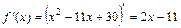 , то по геометрическому смыслу производной функции угловой коэффициент касательной, проведенной к графику этой функции в точке (3; 6) равен
, то по геометрическому смыслу производной функции угловой коэффициент касательной, проведенной к графику этой функции в точке (3; 6) равен  .
.
Уравнение касательной согласно формуле (3) имеет вид:
у – 6 = –5(х – 3) или у = –5 х + 21.
По формуле (4) уравнение нормали имеет вид:
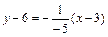 или
или 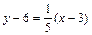 или
или  .
.
Ответ: у = –5 х + 21 – уравнение касательной;  – уравнение нормали.
– уравнение нормали.
Пусть материальная точка М движется прямолинейно по закону S = S (t), где t – время движения, S (t) – путь, пройденный за время t. Производная 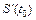 от пути по времени имеет физический смысл мгновенной скорости при прямолинейном движении.
от пути по времени имеет физический смысл мгновенной скорости при прямолинейном движении.
Пример 5. Материальная точка движется прямолинейно по закону 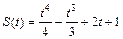 , где S – в метрах, t – в секундах. Найдите скорость движения данной точки в момент времени t 0 = 2 с.
, где S – в метрах, t – в секундах. Найдите скорость движения данной точки в момент времени t 0 = 2 с.
Решение. Вычислим производную от пути по времени:  . Согласно физическому смыслу производной скорость в момент времени t 0 = 2 с равна
. Согласно физическому смыслу производной скорость в момент времени t 0 = 2 с равна 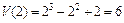 м/с.
м/с.
Ответ: 6 м/с.
Выражение 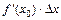 называется дифференциалом функции f (x) в точке х 0 и обозначается символом
называется дифференциалом функции f (x) в точке х 0 и обозначается символом 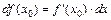 , где по определению обозначено dx = D x.
, где по определению обозначено dx = D x.
Дифференциал функции имеет геометрический смысл части приращения функции f (x) в точке х 0 при перемещении не по графику функции, а по графику касательной, проведенной в точке (x 0; f (x 0)) (рис. 2).
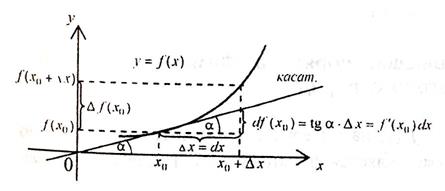
Рис. 2
Если дифференциал вычисляется в произвольной точке х, то 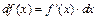 .Отсюда следует другое обозначение производной
.Отсюда следует другое обозначение производной  как отношение дифференциала функции к дифференциалу независимой переменной.
как отношение дифференциала функции к дифференциалу независимой переменной.
Пример 6. Найдите дифференциал функции 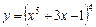 .
.
Решение. Вычислим производную:
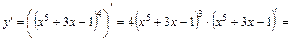
 .
.
Тогда дифференциал равен 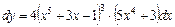 .
.
Ответ: 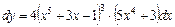 .
.
Пусть функция y = f (x) на интервале (a; b) имеет производную  , которая также является функцией от х и называется производной первого порядка.
, которая также является функцией от х и называется производной первого порядка.
Если функция 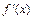 дифференцируема, то ее производная называется производной второго порядка и обозначается символами
дифференцируема, то ее производная называется производной второго порядка и обозначается символами 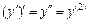 .
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается 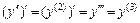 .
.
Аналогично определяются производные 4-го, 5-го и т. д. n -го порядка. Производные порядка выше первого называются производными высших порядков.
Производные 2-го порядка от функций, заданных неявно и параметрически, определяются аналогично как производные от производных первого порядка.
Пример 7. Найдите производную второго порядка функции:
а)  ; б) х 2 + у 2 = 1; в)
; б) х 2 + у 2 = 1; в) 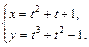
Решение. а) Вычислим первую производную, используя формулу (1) и таблицу производных:
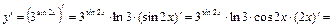
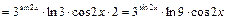 .
.
Теперь найдем вторую производную по правилу производной произведения, формуле (1) и таблицы производных:
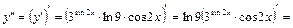
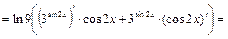
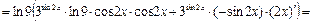
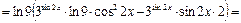
|
|
|
 .
.
б) Найдем первую производную функции, заданной неявно:
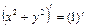 ,
,
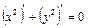 ,
,
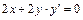 ,
,
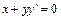 ,
,
 ,
,
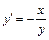 .
.
Найдем вторую производную:
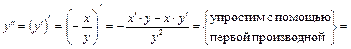
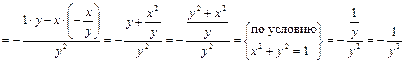 .
.
в) Вычислим по формуле (2) первую производную функции, заданной параметрически: 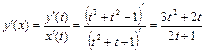 .
.
Вторую производную найдем по формуле 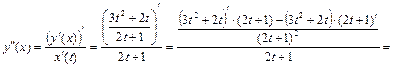
 .
.
Ответ: а)  ; б)
; б) 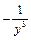 ; в)
; в) 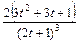 .
.
Пусть материальная точка М движется прямолинейно по закону S = S (t) со скоростью 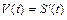 , где t – время движения, S (t) – путь, пройденный за время t. Вторая производная
, где t – время движения, S (t) – путь, пройденный за время t. Вторая производная 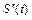 от пути по времени имеет физический смысл ускорения точки при ее прямолинейном и неравномерном движении. Если же точка движется равномерно, т.е. с постоянной скоростью V (t) = const, то
от пути по времени имеет физический смысл ускорения точки при ее прямолинейном и неравномерном движении. Если же точка движется равномерно, т.е. с постоянной скоростью V (t) = const, то 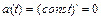 .
.
Пример 8. Дано уравнение движения некоторой точки 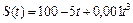 , где S – в метрах, t – в секундах. Найдите ускорение этой точки в момент времени t 0 = 3 с.
, где S – в метрах, t – в секундах. Найдите ускорение этой точки в момент времени t 0 = 3 с.
Решение. Найдем вторую производную от пути по времени: 
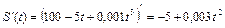 ,
, 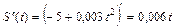 . Тогда по физическому смыслу второй производной ускорение точки равно:
. Тогда по физическому смыслу второй производной ускорение точки равно: 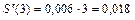 м/с2.
м/с2.
Ответ: 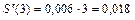 м/с2.
м/с2.
Дифференциал от дифференциала первого порядка называется дифференциалом второго порядка и обозначается 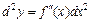 . Аналогично определяются дифференциалы 3-го, 4-го и т. д. порядка. Отсюда следует другое обозначение производных высших порядков:
. Аналогично определяются дифференциалы 3-го, 4-го и т. д. порядка. Отсюда следует другое обозначение производных высших порядков: 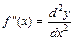 ,
, 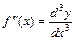 и т. д.
и т. д.
Пример 9. Вычислите дифференциал второго порядка функции 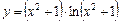 .
.
Решение. Найдем первую и вторую производные:
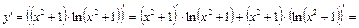
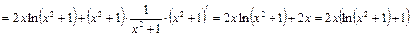 ,
,
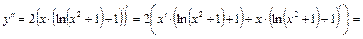
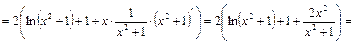
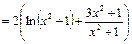 .
.
Т. о., дифференциал второго порядка равен:
 .
.
Ответ: 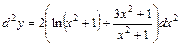 .
.
Правило Лопиталя. Пусть отношение  представляет собой неопределенность вида
представляет собой неопределенность вида  или
или  при х ® х 0, где х 0 – точка или ¥. Тогда предел отношения функций равен пределу отношения их производных:
при х ® х 0, где х 0 – точка или ¥. Тогда предел отношения функций равен пределу отношения их производных: 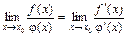 . Если отношение
. Если отношение 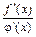 вновь представляет собой неопределенность вида
вновь представляет собой неопределенность вида  или
или  , то правило Лопиталя можно применить повторно до исчезновения неопределенности и, вообще говоря, любое конечное число раз.
, то правило Лопиталя можно применить повторно до исчезновения неопределенности и, вообще говоря, любое конечное число раз.
Пример 10. Найдите  по правилу Лопиталя.
по правилу Лопиталя.
Решение. 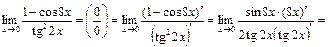
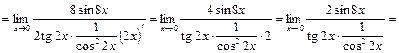
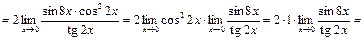
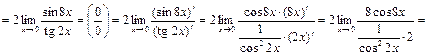
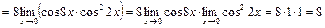 .
.
Указание. Правило Лопиталя использовали два раза.
Ответ:  .
.
***
Настройка окон программы MathCAD для вычисления производных функций:
· На главной панели инструментов Math нажмите на кнопки  и
и  (если главной панели инструментов на экране нет, то V iew ® Toolbars ® M ath). Первая кнопка открывает панель Calculator, а вторая – панель Calculus.
(если главной панели инструментов на экране нет, то V iew ® Toolbars ® M ath). Первая кнопка открывает панель Calculator, а вторая – панель Calculus.
|
|
|
Для вычисления производной функции:
· Выберите нужную кнопку 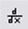 или
или 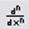 на панели Calculus. Первая кнопка используется для вычисления первой производной, а вторая – для производной высшего порядка.
на панели Calculus. Первая кнопка используется для вычисления первой производной, а вторая – для производной высшего порядка.
· В появившемся шаблоне заполните все поля, используя, если нужно, панель Calculator.
· Введите знак «®», набранный с клавиатуры с помощью комбинации клавиш Ctrl+«×» и щелкните на свободном поле.
4. Индивидуальные задания
Таблица 1
| № вар. | А) | Б) | В) | Г) |
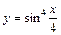
| 
| 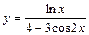
| 
| |
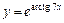
| 
| 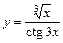
| 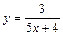
| |
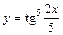
| 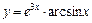
| 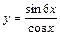
| 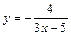
| |

| 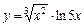
| 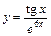
| 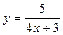
| |
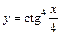
| 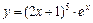
| 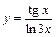
| 
| |
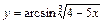
| 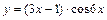
| 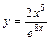
| 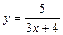
| |
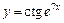
| 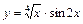
| 
| 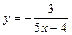
| |
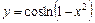
| 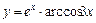
| 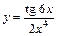
| 
| |
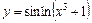
| 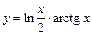
| 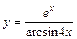
| 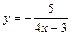
| |
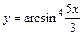
| 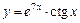
| 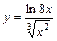
| 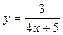
| |
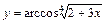
| 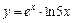
| 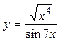
| 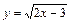
| |
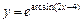
| 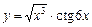
| 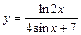
| 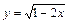
|
Продолжение табл. 1
| № вар. | А) | Б) | В) | Г) |

| 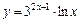
| 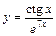
| 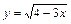
| |
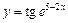
| 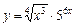
| 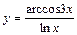
| 
| |
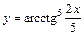
| 
| 
| 
| |

| 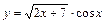
| 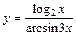
| 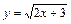
| |
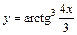
| 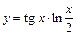
| 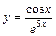
| 
| |
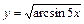
| 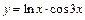
| 
| 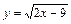
| |
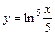
| 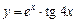
| 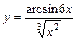
| 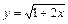
| |
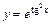
| 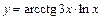
| 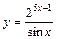
| 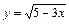
| |
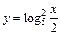
| 
| 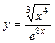
| 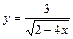
| |
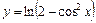
| 
| 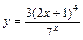
| 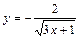
| |
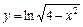
| 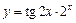
| 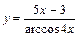
| 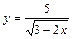
| |
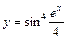
| 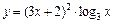
| 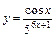
| 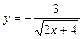
| |
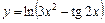
| 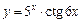
| 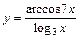
| 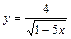
| |
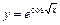
| 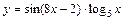
| 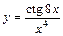
| 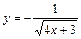
|
Таблица 2
| № вар. | А) | Б) |
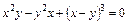
| 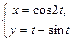
| |
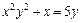
| 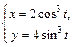
| |
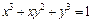
| 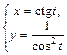
| |
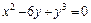
| 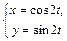
| |

| 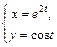
| |
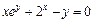
| 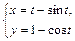
| |
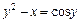
| 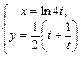
| |

| 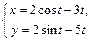
| |
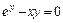
| 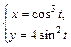
| |
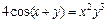
| 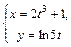
| |
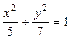
| 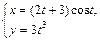
| |
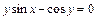
| 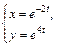
| |
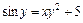
| 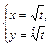
| |
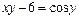
| 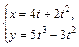
|
Продолжение табл. 2
| № вар. | А) | Б) |
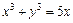
| 
| |
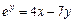
| 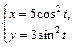
| |
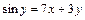
| 
| |
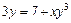
| 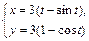
| |
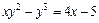
| 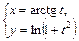
| |
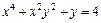
| 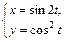
| |
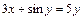
| 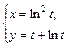
| |
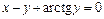
| 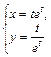
| |
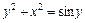
| 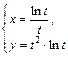
| |
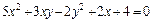
| 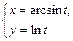
| |
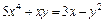
| 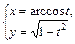
| |
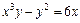
| 
|
Таблица 3
| № вар. | y = f (x) | х 0 | № вар. | y = f (x) | х 0 |
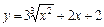
| –1 | 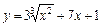
| |||
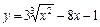
| 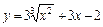
| –1 | |||
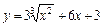
| –1 | 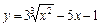
| |||
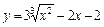
| 
| –1 | |||

| –1 | 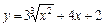
| |||
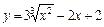
| 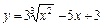
| –1 | |||

| –1 | 
| |||
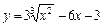
| 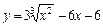
| –1 | |||
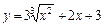
| –1 | 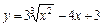
| |||
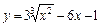
| 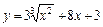
| –1 | |||
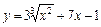
| –1 | 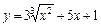
| |||

| 
| –1 | |||
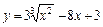
| –1 | 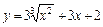
|
Таблица 4
| № вар. | S = S (t) | t 0 | № вар. | S = S (t) | t 0 |
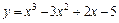
| 
| ||||
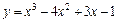
| 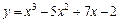
| ||||
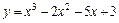
| 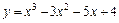
| ||||
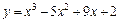
| 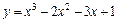
| ||||
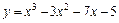
| 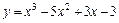
| ||||
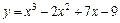
| 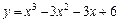
| ||||

| 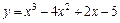
| ||||

| 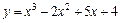
| ||||
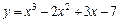
| 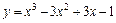
| ||||
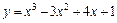
| 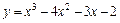
|
Продолжение табл. 4
| № вар. | S = S (t) | t 0 | № вар. | S = S (t) | t 0 |
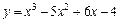
| 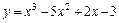
| ||||
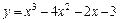
| 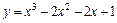
| ||||
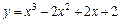
| 
|
Таблица 5
| № вар. | y = f (x) | № вар. | y = f (x)) |
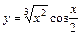
| 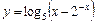
| ||
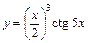
| 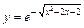
| ||
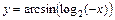
| 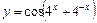
| ||

| 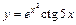
| ||
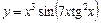
| 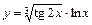
| ||

| 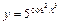
| ||
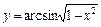
| 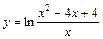
| ||

| 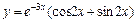
| ||
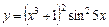
| 
| ||
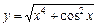
| 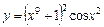
| ||
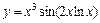
| 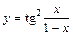
| ||
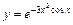
| 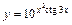
| ||
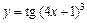
| 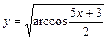
|
 2015-10-22
2015-10-22 837
837








