Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений элементарных высказываний, входящих в формулу. Запись A = B означает, что формулы А и В равносильны. Например, очевидно, что равносильны формулы:
Х = X; Х & Х = X; Х &0=0; Х Ú1=1; Х Ú  =1; X Ú Х = X; X &1= X; X Ú0= X; X &
=1; X Ú Х = X; X &1= X; X Ú0= X; X &  =0.
=0.
Легко видеть, что если А = В, то  .
.
Формула А называется тождественно истинной (или тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных. Например, тождественно истинной является формула X ®(Y ® X), что можно проверить, построив таблицу истинности.
Формула называется тождественно ложной, если она принимает значение ноль при всех значениях входящих в нее переменных. Как уже отмечалось  , то есть формула тождественно ложная.
, то есть формула тождественно ложная.
Из определения равносильных формул следует, что отношение равносильности обладает свойствами:
1. А=А (рефлексивно);
2. Если A=В, то B=A (симметрично);
3. Если А=В и B=С, то A=С (транзитивно).
|
|
|
Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула А «В тавтология (то есть тождественно истинная), и, обратно, если формула А «В тавтология, то формулы А и В равносильны.
Действительно, пусть А = В. Тогда эти формулы принимают одинаковые логические значения на любом наборе значений элементарных высказываний, входящих в формулы и, значит, формула А «В тождественно истинна. Очевидна справедливость и обратного утверждения.
Равносильности, выражающие одни логические операции через другие:
1. X «Y =(X ® Y)×(Y ® X) или X «Y =  2. X ® Y =
2. X ® Y =  3.
3. 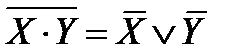 4.
4.  5.
5.  6.
6. 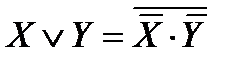
|
Ясно, что равносильности 5 и 6 получаются из равносильностей 3 и 4 соответственно, если от обеих частей равносильностей 3 и 4 взять отрицания и затем воспользоваться законом двойного отрицания ( ). Таким образом, в доказательстве нуждаются первые четыре равносильности. Докажем три из них: первую, вторую и третью.
). Таким образом, в доказательстве нуждаются первые четыре равносильности. Докажем три из них: первую, вторую и третью.
Так как при одинаковых логических значениях X и Y истинными являются формулы X «Y, X ® Y, Y ® X, то истинной будет и конъюнкция (X ® Y)×(Y ® X). Следовательно, в этом случае обе части равносильности 1 имеют одинаковые истинные значения.
Пусть теперь X и Y имеют различные логические значения. Тогда будут ложными эквивалентность X «Y и одна из двух импликаций X ® Y или Y ® X. Но при этом будет ложной и конъюнкция (X ® Y)×(Y ® X). Таким образом, и в этом случае обе части равносильности 1 имеют одинаковые (ложные) значения.
Рассмотрим равносильность 2. При Y =1, очевидно, что  = 1 и X ® Y = 1, то есть обе части равносильности 2 имеют одинаковые значения.
= 1 и X ® Y = 1, то есть обе части равносильности 2 имеют одинаковые значения.
Пусть теперь Y = 0. Тогда при X =1, X ® Y =0 и  = 0, а при X = 0 X ® Y = 1 и
= 0, а при X = 0 X ® Y = 1 и  =1. Значит, и при Y = 0 обе части равносильности 2 имеют одинаковые значения. Этим исчерпывается доказательство равносильности 2.
=1. Значит, и при Y = 0 обе части равносильности 2 имеют одинаковые значения. Этим исчерпывается доказательство равносильности 2.
|
|
|
Рассмотрим равносильность 3. Если X и Y принимают одновременно истинные значения, то будет истинной конъюнкция X × Y и ложной отрицание конъюнкции  .
.
В то же время будут ложными и 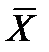 , и
, и  , а поэтому будет ложной и дизъюнкция
, а поэтому будет ложной и дизъюнкция  .
.
Пусть теперь хотя бы одна из переменных X или Y принимает значение ложное. Тогда будет ложна конъюнкция X × Y и истинной ее отрицание. В то же время отрицание хотя бы одной из переменных будет истинным, а поэтому будет истинной и дизъюнкция  .
.
Следовательно, во всех случаях обе части равносильности 3 принимают одинаковые значения.Аналогично доказывается равносильность 4.
Изприведенныхравносильностей следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логических операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.
В самом деле, равносильность 1 позволяет заменить эквивалентность на импликацию и конъюнкцию, равносильность 2 позволяет заменить импликацию на дизъюнкцию и отрицание. Таким образом, после указанных замен в формуле будут использоваться только три операции: конъюнкция, дизъюнкция и отрицание. Если далее воспользоваться равносильностью 5, заменяя конъюнкцию на дизъюнкцию и отрицание, то в формуле будут использоваться только две операции: дизъюнкция и отрицание. Аналогично, если воспользоваться равносильностью 6, то в формуле останется также две операции: конъюнкция и отрицание. Дальнейшее исключение логических операций невозможно. Однако существуют операции, через которые может быть выражена любая из пяти логических операций, которыми мы пользуемся. Такой операцией является, например, операция «штрих Шеффера». Эта операция обозначается символом X | Y и определяется следующей таблицей истинности.
| X | Y | X | Y |
Очевидно, что имеют место равносильности:  = X | X, X × Y =(X | Y)|(X | Y).
= X | X, X × Y =(X | Y)|(X | Y).
Из этих двух равносильностей следует, что всякая формула алгебры логики может быть заменена равносильной формулой, содержащей только операцию «штрих Шеффера». Отметим, что X | Y =  .
.
Аналогично операции «штрих Шеффера» может быть использована операция, называемая «стрелкой Пирса»:  .
.
 2018-01-08
2018-01-08 1072
1072








