Операции с матрицами: транспонирование матрицы, умножение матрицы на число, сложение матриц, умножение матриц, возведение в степень

Арифметические векторы и линейные операции над ними.

Арифметическим n-мерным вектором называется любая последовательность из n действительных чисел (a_1,a_2,..a_n).

Линейные операции над векторами:

1. а + b = b + а (коммутативность сложения/переместительный закон);

2. (a + b) + c = a + (b + c) (ассоциативность сложения/сочетательный закон);

3. α ⋅ (β ⋅a) = (αβ)⋅a (ассоциативность умножения);

4. α ⋅ (a + b) =α a +α b(дистрибутивность относительно сложения векторов);

5. (α +β)a =α a +β a (дистрибутивность относительно сложения чисел);

6. а + 0 = а, где 0 = (0, 0,..., 0);

7. 1⋅a = a, для всех a.

8. Для всех a существует вектор − a, такой, что a + (−a) = 0.

Линейная зависимость системы векторов и ее геометрический смысл.

Система векторов a₁,a₂,..., a_m называется линейно зависимой, если существуют такие числа λ₁,λ₂,...,λ_n, неравные одновременно 0, такие что линейная комбинация векторов λ₁a₁ +λ₂a₂+...+λ_na_n =0 (т.е. обращается в нулевой вектор). В противном случае эти векторы линейно независимы.

Справедливы следующие свойства линейной зависимости:

1) если среди векторов системы есть нулевой вектор, то система линейно зависима;

2) если система векторов содержит линейно зависимую подсистему, то она линейно зависима;

3) любая подсистема линейно независимой системы векторов является линейно независимой;

4) для того, чтобы система векторов a₁,a₂,...,a_m была линейно зависимой, необходимо и достаточно, чтобы хотя бы один из векторов линейно выражался через остальные;

5) диагональная система векторов линейно независима;

6) диагональная система единичных векторов n-мерного пространства линейно независима;

7) любой вектор n-мерного пространства является комбинацией единичных векторов этого пространства.

Матрицы и их виды.

Матрицей размера m× n называется совокупность mn действительных чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов:

Матрица, состоящая из одной строки, называется матрицей – строкой или строчной матрицей: А=(a₁₁a₁₂,…,а_1n). Матрица, содержащая один столбец, называется матрицей – столбцом или столбцевой матрицей:

Матрица называется квадратной n-го порядка, если число её строк, равно числу столбцов и равно n:

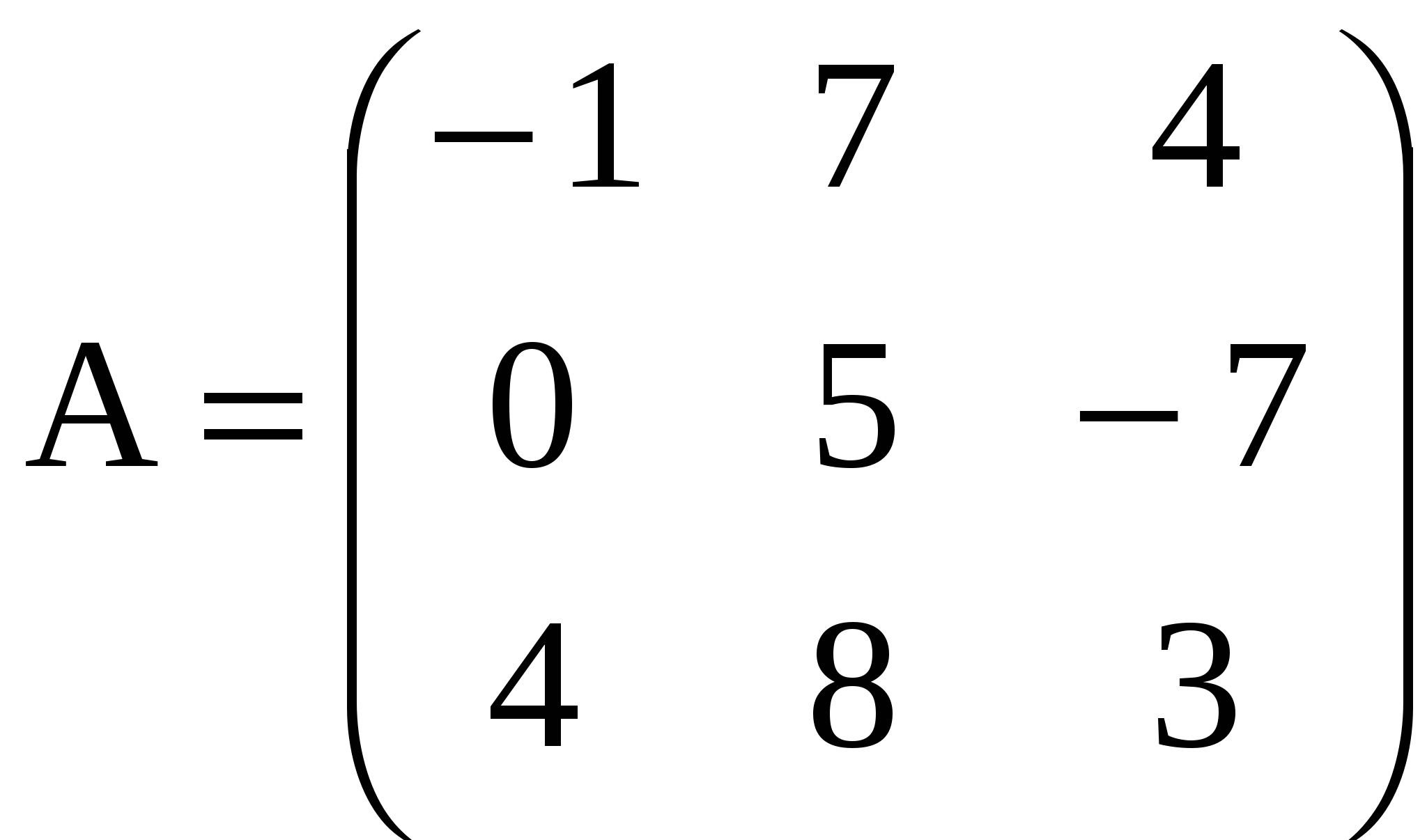- квадратная матрица третьего порядка.

Элементы матрицы a_ij, у которых номер столбца равен номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы. Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной:

- диагональная матрица третьего порядка.

Если у диагоальной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка:

- единичная матрица третьего порядка.

Матрица любого размера называется нулевой, если все её элементы равны нулю:

Операции с матрицами: транспонирование матрицы, умножение матрицы на число, сложение матриц, умножение матриц, возведение в степень.

1) Умножение матрицы на число. Произведением матрицы A на число λ называется матрица B= λA. Общий множитель всех элементов матрицы можно выносить за знак матрицы.

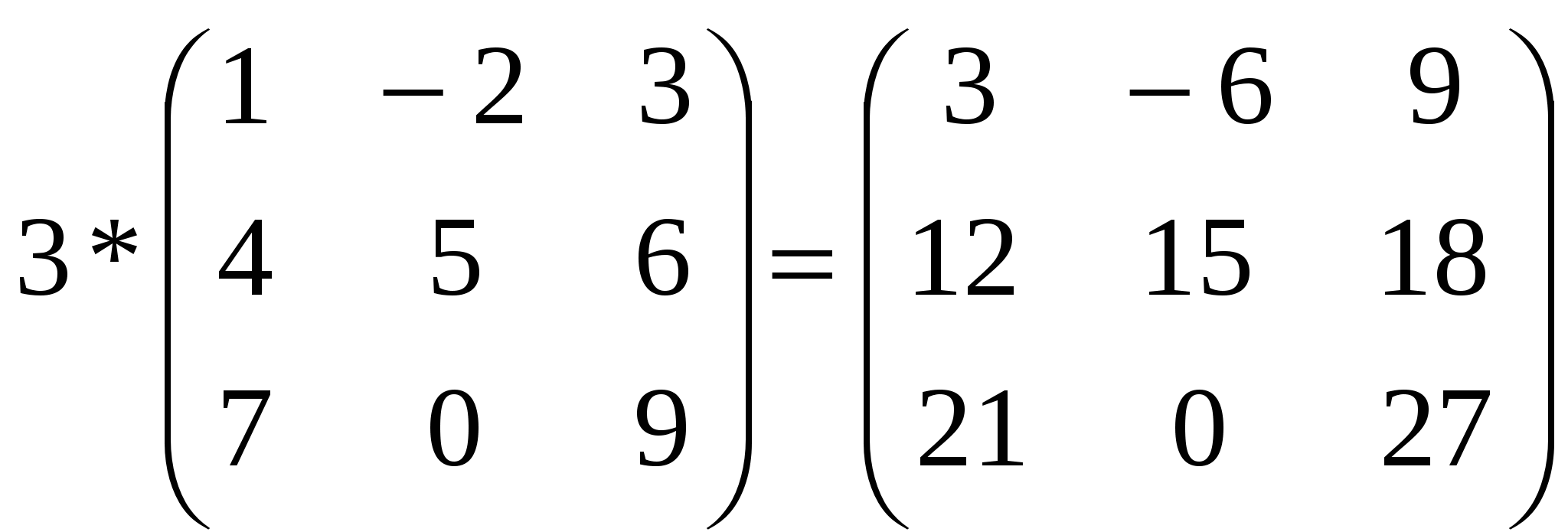
2) Сложение матриц. Суммой двух матриц A и B одинакового размера mxn называется матрица C=A+B, если с_ij=a_ij+b_ij(i=1,…,m, j=1,…,n).

3) Вычитание матриц. Разность двух матриц одинакового размера определяется аналогично сложению.

4) Умножение матриц. Операция умножение матрицы A на матрицу B определена, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A и В называется такая матрица С, каждый элемент которой равен сумме произведений i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.

5) Возведение в степень. Целой положительной степенью А^m(m>1) квадратной матрицы А называется произведение m матриц равных А. Операция возведения в степень определяется только для квадратных матриц.

А⁰=E; А¹=А; А^m × А^k =A^m+k; (A^m)^k =A^mk.

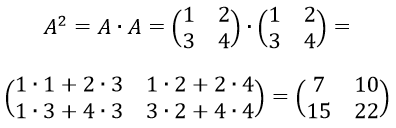
6) Транспонирование матрицы. Под этой операцией понимают переход от матрицы А к матрице А', в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А' называется транспонированной относительно матрицы А:

 

7) След матрицы. Следом квадратной матрицы А называется сумма её диагональных элементов.

Определители матриц и их свойства: формулы для определителей матриц 2-го и 3-го порядков, разложение определителя по строке или столбцу, нахождение определителя методом элементарных преобразований.

Каждой квадратной матрице можно поставить в соответствие некоторое число, вычисляемое по определенному правилу и называемое определителем. Необходимость введения понятия определителя, характеризующего квадратную матрицу порядка n, тесно связано с решением систем линейных алгебраических уравнений.

Определителем матрицы первого порядка А = (а11) называется элемент а11. Например, для А = (-4) имеем |А| = -4.

Определителем матрицы второго порядка называется число, определяемое по формуле: |А| = Например, |А| =

Определителем матрицы третьего порядка называется число, определяемое по формуле:

Это число представляет алгебраическую сумму шести произведений, при этом у первых трех произведений знак не меняется, а у последних – меняется на противоположный. Формулу можно легко запомнить, используя следующую схему, называемую правилом треугольника или правилом Сарруса:

Теорема (о разложении определителя/ Лапласа). Определитель квадратной матрицы равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения:

|А| = а_i1A_i1 + а_i2A_i2 + … + а_inA_in (разложение по элементам i-й строки; i= 1, 2, …, n).

Или

|А| = а_1jA_1j + а_2jA_2j + … + а_njA_nj(разложение по элементам j-го столбца; j = 1,2…, n).

Метод элементарных преобразований заключается в том, чтобы при помощи элементарных преобразований, учитывая свойства определителей, привести матрицу к треугольному виду. Элементарными преобразованиями матрицы называются следующие преобразования: 1) отбрасывание любой строки/столбца; 2) умножение всех элементов строки/столбца матрицы на число неравное 0; 3) изменение порядка строк/столбцов матриц; 4) прибавление к каждому элементу одной строки/столбца к соответствующему результату другого столбца/строки на любое число; 5) транспонирование матриц.