Досить універсальним методом розв’язку лінійних однорідних систем з сталими коефіцієнтами є матричний метод. Він полягає в наступному. Розглядається лінійна система з сталими коефіцієнтами, що записана у векторно-матричному вигляді 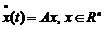 . Робиться невироджене перетворення
. Робиться невироджене перетворення 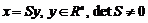 , де вектор
, де вектор  - нова невідома векторна функція. Тоді рівняння прийме вигляд
- нова невідома векторна функція. Тоді рівняння прийме вигляд 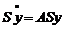 або
або 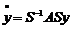 . Для довільної матриці
. Для довільної матриці  завжди існує неособлива матриця
завжди існує неособлива матриця 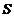 , що приводить її до жорданової форми, тобто
, що приводить її до жорданової форми, тобто 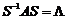 , де
, де 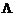 - жорданова форма матриці
- жорданова форма матриці  . І система диференціальних рівнянь прийме вигляд
. І система диференціальних рівнянь прийме вигляд 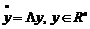 . Складемо характеристичне рівняння матриці
. Складемо характеристичне рівняння матриці  :
:  , або
, або  . Алгебраїчне рівняння
. Алгебраїчне рівняння 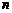 -го ступеня має
-го ступеня має 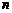 коренів. Розглянемо різні випадки.
коренів. Розглянемо різні випадки.
1. Нехай 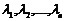 - дійсні різні числа. Тоді матриця
- дійсні різні числа. Тоді матриця 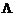 має вигляд
має вигляд  . І перетворена система диференціальних рівнянь розпадається на
. І перетворена система диференціальних рівнянь розпадається на  - незалежних рівнянь
- незалежних рівнянь  .
.
Розв’язуючи кожне окремо, отримаємо  . Або в матричному вигляді
. Або в матричному вигляді
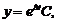 де
де  . Звідси розв’язок вихідного рівняння має вигляд
. Звідси розв’язок вихідного рівняння має вигляд 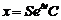 . Для знаходження матриці
. Для знаходження матриці  треба розв’язати матричне рівняння
треба розв’язати матричне рівняння 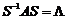 або
або 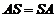 , де
, де 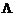 - жорданова форма матриці
- жорданова форма матриці  . Якщо матрицю
. Якщо матрицю  записати у вигляді
записати у вигляді 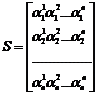 , то для кожного з стовпчиків
, то для кожного з стовпчиків 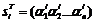 , матричне рівняння перетвориться до
, матричне рівняння перетвориться до 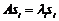 ,
, 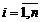 . Таким чином, у випадку різних дійсних власних чисел матриця
. Таким чином, у випадку різних дійсних власних чисел матриця  являє собою набір
являє собою набір 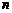 - власних векторів, що відповідають різним власним числам.
- власних векторів, що відповідають різним власним числам.
|
|
|
2. Нехай  - комплексний корінь. Тоді відповідна клітка Жордана має вигляд
- комплексний корінь. Тоді відповідна клітка Жордана має вигляд  ,
,
а перетворена система диференціальних рівнянь  Неважко перевірити, що розв’язок отриманої системи диференціальних рівнянь має вигляд
Неважко перевірити, що розв’язок отриманої системи диференціальних рівнянь має вигляд 
Або в матричному вигляді 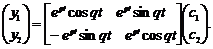 Таким чином, комплексно-спряженим власним числам
Таким чином, комплексно-спряженим власним числам  відповідає розв’язок
відповідає розв’язок 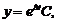 де
де 
3. Нехай  - кратний корінь, кратності
- кратний корінь, кратності 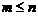 , тобто
, тобто 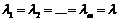 і йому відповідають
і йому відповідають 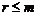 лінійно незалежних векторів. Тоді клітка Жордана, що відповідає цьому власному числу, має вид
лінійно незалежних векторів. Тоді клітка Жордана, що відповідає цьому власному числу, має вид
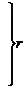
|

І перетворена підсистема, що відповідає власному числу  , розпадається не дві підсистеми
, розпадається не дві підсистеми
 .
.  . Розв’язок першої знаходиться з використанням зазначеного в першому пункті підходу. Розглянемо другу підсистему. Запишемо її в координатному вигляді
. Розв’язок першої знаходиться з використанням зазначеного в першому пункті підходу. Розглянемо другу підсистему. Запишемо її в координатному вигляді 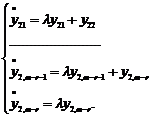 Розв’язок останнього рівняння цієї підсистеми має вигляд
Розв’язок останнього рівняння цієї підсистеми має вигляд 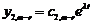 .
.
Підставимо його в передостаннє рівняння. Одержуємо  . Загальний розв’язок лінійного неоднорідного рівняння має вигляд суми загального розв’язку однорідного і частинного розв’язку неоднорідних рівнянь, тобто
. Загальний розв’язок лінійного неоднорідного рівняння має вигляд суми загального розв’язку однорідного і частинного розв’язку неоднорідних рівнянь, тобто 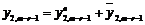 . Загальний розв’язок однорідного має вигляд
. Загальний розв’язок однорідного має вигляд 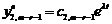 .
.
Частинний розв’язок неоднорідного шукаємо методом невизначених коефіцієнтів у вигляді 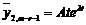 ,
,
де  - невідома стала. Підставивши в неоднорідне рівняння, одержимо
- невідома стала. Підставивши в неоднорідне рівняння, одержимо  .
.
Звідси 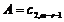 і загальний розв’язок неоднорідного рівняння має вигляд
і загальний розв’язок неоднорідного рівняння має вигляд 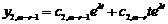 .
.
Піднявшись ще на один крок нагору одержимо 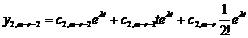 . Продовжуючи процес далі, маємо
. Продовжуючи процес далі, маємо 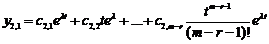 . Або у векторно - матричному вигляді
. Або у векторно - матричному вигляді
|
|
|
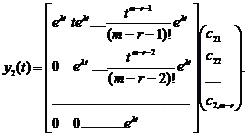 . Додавши першу підсистему, одержимо
. Додавши першу підсистему, одержимо
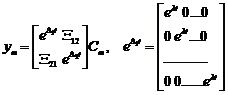 ,
, 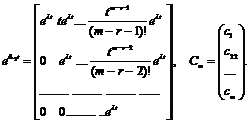
Для останніх двох випадків матриця  знаходиться як розв’язок матричного рівняння
знаходиться як розв’язок матричного рівняння 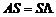 .
.
5.Представлення розв’язку лінійних неоднорідних систем за допомогою формули Коши. Лінійні неоднорідні системи
Система диференціальних рівнянь, що записана у вигляді 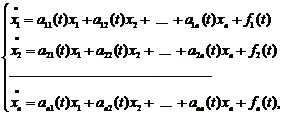
У векторній формі
 ;
; 
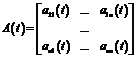
 називається системою лінійних неоднорідних диференціальних рівнянь.
називається системою лінійних неоднорідних диференціальних рівнянь.
 2018-01-21
2018-01-21 488
488









