Задача 1. Множество Е содержит 10 первых букв русского алфавита. Сколько различных алфавитов из трех букв можно составить из данного множества букв? Какова вероятность того, что случайно выбранный алфавит будет содержать букву а?
Решение. Число различных алфавитов равно числу 3-элементных подмножеств множества Е (числу сочетаний из 10 элементов по 3):
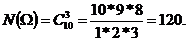
Событие А = {случайно выбранный алфавит из трех букв содержит букву а }. Число элементов множества А равно числу всех возможных способов отобрать две буквы из девяти (из десяти букв исключена буква а, входящая в состав А), т.е. равно числу сочетаний из 9 элементов по 2:
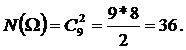
Таким образом, 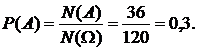
Задача 2. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают 3 изделия для контроля. Найти вероятности следующих событий: A = {в полученной выборке ровно одно изделие бракованное}, В = {в полученной выборке нет ни одного бракованного изделия}.
Решение. Занумеруем изделия числами от 1 до 10, и пусть множество номеров 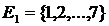 соответствует годным изделиям, а множество
соответствует годным изделиям, а множество 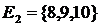 - бракованным изделиям.
- бракованным изделиям.
|
|
|
Согласно описанию эксперимента производится выбор без возвращения и без упорядочивания трех элементов из множества 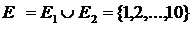 . Поэтому
. Поэтому 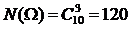 .
.
Событию А благоприятствуют только такие исходы, когда один элемент выборки принадлежит 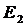 , а остальные два элемента – множеству
, а остальные два элемента – множеству 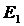 . По формуле прямого произведения множеств получаем, что число всех таких исходов
. По формуле прямого произведения множеств получаем, что число всех таких исходов 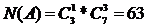 , поэтому
, поэтому
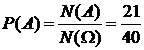 .
.
Событию В благоприятствуют только такие исходы, когда все три отобранных элемента принадлежат множеству 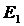 , поэтому
, поэтому 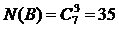 . Отсюда следует, что
. Отсюда следует, что
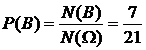 .
.
Задачи.
2.1. Из полного набора домино (28 штук) наудачу выбирают
7 костей. Какова вероятность, что среди них окажется по крайней
мере одна кость с шестью очками?
2.2. Из десяти первых букв русского алфавита наудачу составляется новый алфавит, состоящий из пяти букв. Найти вероятности следующих событий: А = {в состав нового алфавита входит
буква а }, В = {в состав нового алфавита входят только согласные
буквы}.
2.3. Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого со
става наудачу выбирают пять человек на предстоящую конференцию. Найти вероятности следующих событий: А = {будут вы
браны одни третьекурсники}, В = {все первокурсники попадут на
конференцию}, С = {не будет выбрано ни одного второкурсника}.
2.4. Из урны, содержащей т1+m2 шаров, из которых т1 белых и m2 черных, наудачу отбирают т шаров 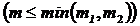 и откладывают в сторону. Найти вероятности следующих событий: А = {все отложенные шары белые}, В = {среди отложенных шаров ровно k белых;
и откладывают в сторону. Найти вероятности следующих событий: А = {все отложенные шары белые}, В = {среди отложенных шаров ровно k белых; 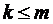 }.
}.
2.5. (продолжение). В условиях предыдущей задачи найти вероятности событий: С = {вынут хотя бы один белый шар}, D = {вынуто не менее k белых шаров; 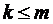 }.
}.
|
|
|
2.6. Для уменьшения числа игр 2 n футбольных команд, среди которых 2 призера предыдущего чемпионата, путем жеребьевки
разбиваются на две подгруппы (первую и вторую) по п команд в
каждой. Какова вероятность qn того, что обе команды-призеры
попадут в разные группы?
2.7. Из колоды в 52 карты извлекаются наудачу 4 карты.
Найти вероятности следующих событий: А = {в полученной выборке все карты бубновой масти}, В = {окажется хотя бы один
туз}, С = {появятся ровно 2 пики}.
2.8. Из урны, содержащей т1 шаров с номером 1, т2 шаров
с номером 2,..., ms шаров с номером s, наудачу без возвращения
извлекается п шаров. Найти вероятности событий: А = {появится
n1 шаров с номером 1, n2 шаров с номером 2,..., ns шаров с
номером s }; В = {не появятся шары с номерами 1 или 2}.
2.9. Два равных по силе противника играют матч из п партий в теннис. Каждая партия заканчивается выигрышем, либо
проигрышем одного из участников. Все исходы данного матча
считаются равновероятными. Найти вероятность того, что первый игрок выиграет ровно т партий  .
.
2.10. В урне а белых и b черных шаров (а 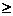 2). Из урны вынимают
2). Из урны вынимают
сразу два шара. Найти вероятность того, что оба шара будут белыми.
2.11. В урне а белых и b черных шаров (а 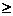 2, b
2, b 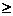 3). Из урны вынимают сразу пять шаров. Найти вероятность р того, что два из них будут белыми, а три черными.
3). Из урны вынимают сразу пять шаров. Найти вероятность р того, что два из них будут белыми, а три черными.
2.12. В партии, состоящей из k изделий, имеется l дефектных. Из
партии выбирается для контроля r изделий. Найти вероятность р того, что из них ровно s изделий будут дефектными.
2.13. Игральная кость бросается один раз. Найти вероятности событий:
А = {четное число очков};
В = {не менее 5 очков};
С = {не более 5 очков}.
2.14. В урне а белых и b черных шаров (а 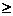 2; b
2; b 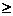 2). Из урны
2). Из урны
вынимают одновременно два шара. Какое событие более вероятно:
А = {шары одного цвета}; В = {шары разных цветов}?
2.15. В розыгрыше первенства по баскетболу участвуют 18 команд,
из которых случайным образом формируются две группы по 9 команд в каждой. Среди участников соревнований имеется 5 команд экстракласса. Найти вероятность следующих событий:
А = {все команды экстракласса попадут в одну и ту же группу};
В = {две команды экстракласса попадут в одну из групп, а три — в другую}.
2.16. Некто купил карточку Спортлото и отметил в ней 6 из имеющихся 49 номеров, после чего в тираже разыгрываются 6 «выигравших» номеров из 49. Найти вероятности следующих событий:
А 3 = {верно угаданы 3 выигравших номера из 6};
А 4 = {верно угаданы 4 номера из 6};
А 5 = {верно угаданы 5 номеров из 6};
А 6 = {верно угаданы все 6 номеров}.
2.17. В пачке 20 перфокарт, помеченных номерами 101, 102,.... 120 и произвольно расположенных. Перфораторщица наудачу извлекает две карты. Найти вероятность того, что извлечены перфокарты с номерами 101 и 120.
2.18. В ящике 10 одинаковых деталей, помеченных номерами 1, 2,..., 10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлеченных деталей окажутся: а) деталь № 1; б) детали № 1 и № 2.
2.19. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
2.20. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.
2.21. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных.
2.22. Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.
2.23. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
|
|
|
2.24. В партии из N деталей имеется п стандартных. Наудачу отобраны т деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных.
2.25. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.
2.26. На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода.
2.27. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.
2.28. В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие.
2.29. В «секретном» замке на общей оси четыре диска, каждый из которых разделен на пять секторов, на которых написаны различные цифры. Замок открывается только в том случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт.
Схема выбора, приводящая к размещениям. Если опыт состоит в выборе m элементов без возвращения, но с упорядочиванием их по мере выбора в последовательную цепочку, то различными исходами данного опыта будут упорядоченные m –элементные подмножества множества Е, отличающиеся либо набором элементов, либо порядком их следования. Получаемые при этом комбинации элементов (элементарные исходы) называются размещениями из n элементов по m, а их общее число определяется формулой

В частном случае m=n опыт фактически состоит в произвольном упорядочивании множества Е, т.е. сводится к случайной перестановке элементов всего множества. При этом 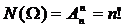
|
|
|
 2018-01-21
2018-01-21 5164
5164








