По теме: Определенный интеграл

1. Вычислить площадь фигуры, ограниченной линиями.

1)

2)

3)

4) (спираль Архимеда).

5)

6)

7) (кардиоида) и полярная ось.

8)

9)

10) и полярная ось.

11)

12)

13)

14) , справа от прямой

15)

16)

17)

18)

19)

20)

21)

22)

23)

24) (одна полуволна),

25)

26)

27) (астроида).

28)

29) (эллипс), справа от прямой

30) (эллипс),

2. Вычислить длину дуги плоской кривой.

1) Одной арки циклоиды

2) Кардиоиды

3) Астроиды

4) Логарифмической спирали где находящейся внутри круга

5) Эволюты (развертки) окружности

6) Полукубической параболы от точки до точки

7)

8) Первого витка спирали Архимеда

9) Одной арки циклоиды

10) Длину параболы 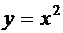при

11) Длину архимедовой спирали (отсчет вести от ).

12) Астроиды

13)

14) Полукубической параболы

15) Петли кривой

16) Эволюты эллипса

17) 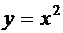от до

18) Цепной линии на отрезке

19)

20) Длину дуги цепной линии при

21)

22) Длину полукубической параболы

23) Полукубической параболы

24) Используя определенный интеграл, доказать, что длина окружности равна

25) Винтовой линии Указание: это пространственная кривая, дифференциал дуги её равен

26) Астроиды

27) Длину параболы

28) от точки до точки

29)

30)

3. Вычислить площадь поверхности.

1) Поверхность образована вращением кардиоиды вокруг полярной оси.

2) Поверхность представляет собой шаровой пояс, получаемый при вращении вокруг оси дуги окружности между точками с абсциссами

3) Поверхность образована вращением лемнискаты вокруг полярной оси.

4) Поверхность образована вращением одной арки циклоиды вокруг касательной, параллельной оси и проходящей через вершину.

5) Поверхность образована вращением вокруг прямой фигуры, ограниченной линиями

6) Поверхность образована вращением первой арки циклоиды вокруг оси

7) Поверхность образована вращением астроиды вокруг оси

8) Поверхность образована вращением вокруг оси кривой

9) Поверхность образована вращением кривой вокруг полярной оси.

10) Поверхность образована вращением кардиоиды вокруг полярной оси.

11) Поверхность образована вращением тангенсоиды от точки с абсциссой до точки с абсциссой вокруг оси

12) Поверхность образована вращением вокруг оси дуги кривой

13) Поверхность представляет собой шаровой пояс, получаемый при вращении вокруг оси дуги окружности между точками с абсциссами

14) Поверхность образована вращением вокруг оси петли кривой

15) Поверхность образована вращением одной арки циклоиды вокруг оси

16) Поверхность образована вращением вокруг оси дуги отсеченной прямой

17) Поверхность образована вращением вокруг оси дуги цепной линии от точки с абсциссой до

18) Поверхность образована вращением вокруг оси части кривой на отрезке, соответствующем

19) Поверхность образована вращением вокруг оси дуги параболы от начала координат до точки с абсциссой

20) Поверхность образована вращением параболы вокруг оси

21) Поверхность образована вращением вокруг оси

22) Поверхность образована вращением вокруг оси дуги параболы от точки с абсциссой до точки с абсциссой

23) Поверхность образована вращением вокруг оси дуги кривой

24) Поверхность образована вращением правой части (относительно оси ) астроиды вокруг оси

25) Поверхность образована вращением вокруг оси дуги кривой от точки с абсциссой до точки пересечения кривой с осью абсцисс

26) Поверхность образована вращением кривой 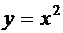вокруг оси от точки с ординатой до точки с ординатой

27) Поверхность образована вращением кривой вокруг оси

28) Поверхность образована вращением одной арки циклоиды вокруг оси

29) Поверхность образована вращением вокруг оси дуги цепной линии от точки с абсциссой до

30) Поверхность образована вращением линии вокруг оси

4. Вычислить объём тела, образованного вращением вокруг некоторой оси фигуры, ограниченной линиями.

1) вокруг оси .

2) Астроиды вокруг оси .

3) вокруг оси .

4) вокруг оси .

5) вокруг оси .

6) вокруг полярной оси.

7) вокруг оси .

8) вокруг оси (справа от оси ).

9) вокруг оси .

10) Астроиды вокруг оси .

11) вокруг полярной оси.

12) вокруг полярной оси.

13) вокруг оси

14) вокруг оси

15) вокруг оси

16) вокруг полярной оси.

17) вокруг оси

18) Циссоиды вокруг оси

19) вокруг оси

20) вокруг оси

21) вокруг оси

22) вокруг оси

23) вокруг полярной оси.

24) Цепной линии вокруг оси

25) вокруг оси

26) Астроиды вокруг оси

27) вокруг оси

28) вокруг оси

29) вокруг полярной оси.

30) вокруг полярной оси.

5. Механические задачи.

1) Определить абсциссу центра тяжести фигуры, ограниченной линиями

2) Определить координаты центра масс части окружности лежащей в первой четверти.

3) Определить массу дуги заключенной между прямыми

4) Вычислить статический момент дуги цепной линии относительно оси

5) Определить ординату центра тяжести пластинки, ограниченной линиями

6) Вычислить координаты центра масс однородной пластины, ограниченной параболой

7) Определить моменты инерции дуги астроиды лежащей в первой четверти.

8) Вычислить координаты центра масс фигуры, ограниченной дугой эллипса расположенной в первой четверти, и осями координат.

9) Вычислить координаты центра масс дуги окружности находящейся под осью

10) Определить координаты центра тяжести фигуры, ограниченной линиями

11) Вычислить центр масс одной арки циклоиды

12) Определить момент инерции относительно трапеции, ограниченной линиями

13) Вычислить момент инерции относительно оси плоской фигуры, ограниченной линиями

14) Вычислить момент инерции полуокружности относительно оси

15) Определить моменты инерции однородной дуги астроиды лежащей в первой четверти.

16) Вычислить момент инерции относительно оси параболического сегмента, ограниченного параболой и прямой

17) Вычислить статические моменты дуги астроиды лежащей в первой четверти.

18) Определить момент инерции относительно оси трапеции, ограниченной линиями

19) Определить координаты центра масс полуокружности расположенной над осью абсцисс.

20) Вычислить статический момент относительно оси пластинки, ограниченной линиями

21) Определить координаты центра масс одной арки циклоиды

22) Вычислить статический момент относительно оси треугольника, ограниченного прямыми

23) Вычислить координаты центра масс дуги цепной линии

24) Определить момент инерции относительно оси дуги

25) Вычислить статический момент относительно оси фигуры, ограниченной дугой полуокружности и осью ординат.

26) Вычислить момент инерции относительно оси фигуры, ограниченной эллипсом

27) Определить статический момент относительно оси треугольника, ограниченного прямыми

28) Вычислить момент инерции фигуры, ограниченной окружностью относительно оси

29) Вычислить статический момент относительно оси дуги кривой

30) Определить момент инерции цепной линии относительно оси

6. Физические задачи.

1) Определить массу стержня длины если линейная плотность меняется по закону где - расстояние точки от одного из концов стержня.

2) В дне цилиндрического сосуда, площадь основания которого а высота имеется отверстие. Вычислить площадь этого отверстия, если вода, доверху наполняющая сосуд, вытекает из него за время

3) За какое время вода, наполовину заполняющая цилиндрический резервуар высоты и радиуса основания вытечет из него, если он лежит на боку, в котором имеется щель площади

4) Вычислить работу, затраченную на выкачивание воды из полностью заполненного сосуда в форме правильной треугольной призмы, имеющей высоту и сторону основания

5) Определить массу пластинки, имеющей форму равнобедренного треугольника со стороной и основанием если поверхностная плотность где - расстояние от точки до прямой, проведенной параллельно основанию через противолежащую ему вершину.

6) За какое время вытечет вода из полностью заполненного сосуда в форме правильной треугольной призмы, если в дне имеется щель площади ? Высота призмы сторона основания

7) Вычислить работу, требующуюся для выкачивания воды из котла, имеющего форму полусферы радиуса

8) Определить массу прямого кругового конуса, высота которого угол между высотой и образующей равен а плотность в каждой точке конуса пропорциональна расстоянию ее от плоскости, проходящей через его вершину параллельно основанию (коэффициент пропорциональности ).

9) Лежащая горизонтальная труба, поперечным сечением которой служит круг диаметром наполовину наполнена водой. Определить силу давления воды на вертикальную заслонку, закрывающую трубу.

10) Вертикальная плотина имеет форму трапеции. Вычислить силу давления воды на плотину, если известно, что верхнее основание равно нижнее основание высота

11) Определить силу давления воды на одну из боковых поверхностей пластинки, имеющей форму полукруга радиуса и погруженной в воду так, что диаметр параллелен поверхности воды, а дуга полуокружности касается поверхности воды.

12) Вычислить работу, затрачиваемую на выкачивание воды из сосуда, имеющего форму прямоугольного параллелепипеда высоты с основанием длиной и шириной

13) Материальная точка массы и однородный стержень длиной и массой лежат на одной прямой. Расстояние от точки до ближнего конца стержня равно Вычислить силу взаимодействия между точкой и стержнем.

14) С какой силой полукольцо радиуса и массой действует на материальную точку массы находящуюся в его центре?

15) Определить силу давления воды на одну из боковых поверхностей вертикального параболического сегмента, основание которого длины расположено на поверхности воды, а вершина – на глубине

16) Определить силу давления воды на пластину, имеющую форму прямоугольного треугольника, катеты которого равны а гипотенуза находится на свободной поверхности воды.

17) Вычислить работу, необходимую для выкачивания воды из корыта длиной имеющего в своем сечении полукруг радиуса

18) Пластинка в форме эллипса наполовину погружена в воду так, что ось длиной расположена на поверхности воды. Какова сила давления на каждую из сторон этой пластинки, если длина погруженной полуоси эллипса

19) Вычислить работу, необходимую для выкачивания воды из прямого кругового конуса высоты и радиуса основания расположенного вершиной кверху.

20) Определить массу пластинки, имеющей форму равнобедренного треугольника с боковой стороной и основанием если поверхностная плотность где - расстояние точки до основания треугольника.

21) Вычислить работу, необходимую для выкачивания воды из сосуда, имеющего форму прямого кругового конуса высоты и радиуса основания перевернутого вверх основанием.

22) Определить силу электростатического взаимодействия проволочного полукольца радиуса по которому равномерно распределен заряд, и единичного точечного заряда, находящегося в его центре.

23) В дне котла, имеющего форму полушара радиуса образовалась пробоина площадью Через какое время вода, доверху наполняющая котел, вытечет из него?

24) Определить массу пластинки, имеющей форму полукруга единичного радиуса, если поверхностная плотность в каждой точке прямо пропорциональна расстоянию до оси симметрии. Коэффициент пропорциональности

25) Определить массу пластины, ограниченной линиями Поверхностная плотность в каждой точке пластины равна

26) Определить силу электростатического взаимодействия точечного заряда и равномерно заряженного стержня длины расположенных на одной прямой. Заряд стержня расстояние от ближайшего конца стержня до заряда равно

27) Вычислить давление воды на пластинку, имеющую форму равнобедренного треугольника с длиной боковой стороны основание длины расположено на свободной поверхности воды.

28) В дне ведра, имеющего форму усеченного прямого кругового конуса с диаметром верхнего основания 2, диаметром нижнего 1, высотой 4, имеется пробоина площадью Через какое время вода, полностью заполнявшая ведро, вытечет из него?

29) Определить работу, затраченную на выкачивание воды, доверху заполняющую ведро в форме усеченного прямого кругового конуса высоты 4. Диаметр нижнего основания 1, верхнего – 2.

30) На какой глубине проходит горизонтальная линия, делящая прямоугольный равнобедренный треугольник с длиной катетов на две части, с одинаковым давлением воды, если он погружен в воду так, что один из его катетов параллелен свободной поверхности воды, а его вершина – касается свободной поверхности воды?

Решение типовых примеров.

1. Площадь плоской фигуры.

а) Кривая задана в декартовых координатах

б) Кривая задана параметрически

в) Кривая задана в полярных координатах

Пример. Вычислить площадь фигуры, ограниченной линиями:

Решение. Делается чертеж.

 

На основании формулы а)

2. Длина дуги плоской кривой.

а) Кривая задана в декартовой системе координат

б) Кривая задана параметрически

в) Кривая задана в полярных координатах

Пример. Вычислить длину кривой

Решение. Определим

Тогда

3. Площадь поверхности тела вращения.

а) Кривая задана в декартовых координатах

б) Кривая задана параметрически

в) Кривая задана в полярных координатах

Пример. Вычислить площадь поверхности, образованной вращением вокруг оси дуги кубической параболы .

Решение.

4. Объем тела вращения.

а) Кривая задана в декартовых координатах

при вращении вокруг оси абсцисс.

При вращении вокруг оси ординат перейти в уравнении кривой к виду и использовать формулу

б) Кривая задана параметрически

при вращении вокруг оси ,

при вращении вокруг оси .

в) Кривая задана в полярных координатах

при вращении вокруг полярной.

Пример. Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной параболой прямыми

Решение.

 

5. Механические задачи.

Если не оговорено специально, то в таких задачах плотность принимается равной единице. В этом случае масса считается равной длине дуги или площади фигуры.

а) Для плоской фигуры, ограниченной кривой осью и прямыми статические моменты относительно осей координат равны: а моменты инерции: В этих формулах - дифференциал площади криволинейной трапеции.

б) Для дуги плоской кривой , соединяющей точки и статические моменты равны: а моменты инерции

в) Координаты центра масс плоской кривой или фигуры на плоскости вычисляются по формулам: где -масса.

Пример. Вычислить статический момент полуокружности относительно оси

Решение. Статический момент вычислим по формуле Сначала вычислим Тогда

6. Физические задачи.

При решении физических задач базируются на известных законах и физических зависимостях:

а) давление жидкости на горизонтальную площадку , где - удельный вес жидкости, - глубина погружения площадки, т.е. расстояние площадки до поверхности жидкости, площадь площадки;

б) величина работы затрачиваемой на поднятие некоторого тела весом на высоту равна ;

в) сила взаимодействия двух (точечных) масс равна , где - массы тел, вектор расстояния между ними (между центрами масс), - коэффициент пропорциональности;

г) кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна , где - момент инерции тела относительно оси вращения, - угловая скорость;

д) за время через маленькое отверстие площадью вытекает объем жидкости где - скорость истечения жидкости из отверстия, расположенного на глубине ;

е) величина силы взаимодействия двух точечных зарядов (закон Кулона) где - величины зарядов, - расстояние между ними, диэлектрическая постоянная.

Пример. При установившемся ламинарном (струйном) течении жидкости через трубу круглого сечения радиуса скорость течения в точке, находящейся на расстоянии от оси трубы, определяется по формуле где - разность давления жидкости на концах трубы, - коэффициент вязкости, - длина трубы. Определить расход жидкости т.е. количество жидкости, протекающей через поперечное сечение трубы в единицу времени.

Решение. Если скорость истечения жидкости одинакова во всех точках сечения площади то расход ее В предложенной задаче Выделим элементарное сечение в виде кольца шириной расположенного на расстоянии от оси трубы. Очевидно, что Интегрируя, получим