2017-11-01
191
, (6)
Здесь 
-первый член прогрессии, 
-знаменатель прогрессии. Найдем 
-ю частичную сумму геометрической прогрессии. Имеем:
,
но
и, следовательно,
,
откуда для искомой -ой частичной суммы прогрессии получаем
. (7)
Найдем предел последовательности частичных сумм:
.
Рассмотрим возникающие частные случаи:
1). 
, тогда 
, а значит и 
, следовательно, 
. То есть при геометрическая прогрессия сходится и ее сумма равна
. (8)
2). 
тогда 
и 
. То есть при геометрическая прогрессия расходится.
3). Если 
, ряд принимает вид 
, его -я частичная сумма равна 
и 
при 
.
4). Если 
, ряд принимает вид 
, его -я частичная сумма равна: 
при 
- четном, и 
при - нечетном. Но это означает, что при любом 
, не равном нулю, последовательность частичных сумм предела не имеет и, следовательно, ряд расходится.
Итак, мы показали, что геометрическая прогрессия сходится при , и расходится при 
.
1 .3 Свойства числовых рядов
Теорема 1. Если ряд
(9)
сходится и имеет сумму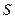 
, то ряд
(10)
полученный из него путем умножения всех его членов на один и тот же постоянный множитель , также сходится и имеет сумму 
.
|
|
|
. Доказательство. ►Пусть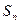 
- -я частичная сумма ряда (9), а 
- -я частичная сумма ряда (10). Тогда:
и, следовательно,
,
что и требовалось доказать. ◄
Теорема 2. Если ряды
(11)
(12)
сходятся и имеют суммы 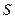и 
, соответственно, то ряд
(13)
полученный почленным суммированием рядов (11) и (12), также сходится и имеет сумму 
.
. Доказательство. ►Пусть 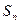- -я частичная сумма ряда (11), а - -я частичная сумма ряда (12). Тогда:
и, следовательно,
,
что и требовалось доказать. ◄
Теорема 3. Если ряд
(14)
сходится и имеет сумму 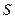, то ряд
(15)
полученный из него отбрасыванием конечного числа 
его первых членов, также сходится и имеет сумму 
, где 
- -я частичная сумма ряда. Обратно, если сходится ряд (15), то будет сходиться и ряд (14), полученный из него приписыванием конечного числа членов.
. Доказательство. ►Пусть 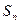- -я частичная сумма ряда (14), а 
- сумма первых 
членов ряда (15). Тогда:
и, следовательно:
1). Если ряд (14) сходится и имеет сумму 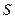, то
,
то есть ряд (15) тоже сходится и имеет сумму .
2). Пусть теперь сходится ряд (15) и имеет сумму 
. Тогда
и
.
что и доказывает теорему. ◄
Следствие. На сходимость ряда не влияет отбрасывание или приписывание конечного числа первых членов.
1.4 Необходимый признак сходимости ряда
При исследовании числовых рядов основным вопросом является вопрос о сходимости ряда. Не вычисляя суммы ряда, ответ на этот вопрос можно получить с помощью, так называемых, необходимых и достаточных признаков сходимости.
Здесь мы рассмотрим необходимый признак сходимости ряда.
|
|
|
Теорема. Если ряд
(16)
сходится, то его общий член стремится к нулю при неограниченном возрастании номера .
. Доказательство. ►Пусть ряд(16) сходится и имеет сумму 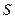. Рассмотрим частичные суммы
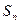и 
:
.
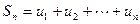
Очевидно, что 
. Но тогда
,
так как
и
.
Итак, если ряд сходится, то
, (17)
что и требовалось доказать. ◄
Следствие. Если общий член ряда 
не стремится к нулю при неограниченном возрастании номера , то такой ряд не может быть сходящимся.
Сформулированный признак сходимости ряда является необходимым, но не является достаточным. То есть, если этот признак не выполняется, то ряд расходится, но если он выполняется, то это не гарантирует сходимости ряда. Другими словами, существуют такие расходящиеся ряды, для которых . В связи с этим, необходимо ввести достаточные признаки сходимости числового ряда.
Лекция 2.
2.1 Достаточные признаки сходимости знакоположительных рядов
Определение. Числовой ряд, все члены которого положительные числа, называется знакоположительным.
Отметим следующую особенность знакоположительного ряда: его частичные суммы
.
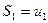
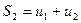
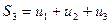
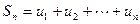
положительны и образуют возрастающую последовательность т.е.
.
2.2 Признаки сравнения
1). Непосредственный признак сравнения
Теорема. Пусть между членами двух знакоположительных рядов (u) и (v)
(18)
(19)
начиная с некоторого номера N выполняются соотношения
. (20)
Тогда, из сходимости ряда (v) следует сходимость ряда (u), а из расходимости ряда (u) следует расходимость ряда (v).
. Доказательство. ► Прежде всего отметим, что совершенно не существенно выполняются ли соотношения (20) для первых 
членов рядов, поскольку, согласно теореме 3, отбрасывание конечного числа первых членов ряда не влияет на его сходимость. Пусть 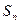и - -е частичные суммы рядов 
и 
соответственно за вычетом их первых членов, т.е.
.
Тогда, в силу соотношений (20),
,
и переходя к пределу при 
, получаем
.
Отсюда следует:
а) если существует и конечен предел последовательности частичных сумм , то существует и конечен и предел последовательности частичных сумм 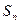, что эквивалентно утверждению: если сходится ряд , то сходится и ряд ;
б) если предел последовательности частичных сумм 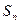не существует или бесконечен, то не существует или бесконечен и предел последовательности частичных сумм , что эквивалентно утверждению: если расходится ряд , то расходится и ряд . Теорема доказана. ◄
Для применения данного признака сравнения нужно располагать эталонными рядами, относительно которых заранее известно сходятся они или расходятся. В качестве таких эталонных рядов наиболее часто применяются:
