Нехай вибірка для дискретної ознаки  задана частотною таблицею (1). Не завжди буває можливим одержати чітке уявлення про ознаку
задана частотною таблицею (1). Не завжди буває можливим одержати чітке уявлення про ознаку  за допомогою великої кількості різних чисел. В цьому випадку виникає потреба користуватися різними середніми величинами (середньою арифметичною, середньою геометричною, середньою гармонійною, середньою кубічною, середньою квадратичною).
за допомогою великої кількості різних чисел. В цьому випадку виникає потреба користуватися різними середніми величинами (середньою арифметичною, середньою геометричною, середньою гармонійною, середньою кубічною, середньою квадратичною).
За допомогою середніх величин велику кількість чисел можна охарактеризувати одним числом,не зважаючи на те,що середня величина абстрактна і може не збігатися з жодним окремим значенням ознаки. Але саме в цій абстракції, у здатності не брати до уваги окремі випадкові значення і відхилення, полягає цінність середніх, як узагальнюючих числових характеристик.
Середня величина відображає те загальне, типове для маси явищ, яке реально існує у реальному світі.
За допомогою середніх можна здійснювати порівняльний аналіз декількох статистичних сукупностей, давати характеристику закономірностям розвитку явищ і процесів.
|
|
|
Самою відомою і широко використовуваною на практиці є середня арифметична (статистична середня або вибіркова середня), що обчислюється за формулою (для згрупованих даних):

 (2) або
(2) або 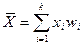 (3)
(3)
Якщо  =1,
=1,  , то формула (2) матиме вигляд
, то формула (2) матиме вигляд
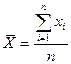 (4).
(4).
Формула (4) може використовуватись і для незгрупованих даних.
Найпростішою числовою характеристикою є мода.
Модою називається те значення вибірки (варіанта), яке найчастіше зустрічається у статистичній сукупності, тобто частота якого найбільша (позначається  ). Отже,
). Отже,  .
.
У випадку, коли всі значення сукупності зустрічаються однаково часто, моди немає. Можуть бути і такі статистичні сукупності,які мають декілька мод(полімодальні сукупності).
Медіаною називається таке значення, яке ділить варіаційний ряд навпіл, так, що варіанти однієї половини є меншими медіани, а варіанти другої половини – більшими медіани (позначається  ),тобто
),тобто 


Зауваження. Числа  ,
,  та
та  - це середні значення вибірки, які є і середніми значеннями дискретної ознаки
- це середні значення вибірки, які є і середніми значеннями дискретної ознаки  .
.
Середня арифметична, мода і медіана співпадають тільки тоді, коли статистичний розподіл унімодальний (з одним максимумом) і симетричний. Чим більше розподіл відрізняється від симетричного, тим більша різниця між цими числовими характеристиками. Для тих випадків, коли статистичний розподіл сильно асиметричний, середня арифметична втрачає свою практичну цінність, оскільки переважна більшість значень варіанти знаходяться ближче або далі від середньої арифметичної. У цьому випадку медіана є характеристикою центра розподілу.
Для вимірювання розсіювання(коливань) ознаки застосовують такі характеристики: варіаційний розмах, статистична дисперсія, статистичне середнє квадратичне відхилення, коефіцієнт варіації.
|
|
|
Варіаційним розмахом (або шириною розподілу) називається різниця між найбільшою і найменшою варіантом, іншими словами, це довжина відрізка на числовій прямій, в середині якого змінюються варіанти (позначається R).
Можна навести багато прикладів розподілів, які різні за будовою, але мають однаковий варіаційний розмах. Цю числову характеристику використовують при статистичному вивченні якості продукції із-за простоти обчислення. 
При обчисленні варіаційного розмаху, так само, як і при обчисленні моди чи медіани, не враховується кожне окреме значення. Тому найчастіше для оцінки міри розсіювання ознаки в теорії та на практиці застосовують інші числові характеристики (дисперсію і середнє квадратичне відхилення).
Статистичною (вибірковою) дисперсією називається середнє арифметичне квадратів відхилень значень вибірки (варіант) від статистичного середнього  і позначається
і позначається  .
.
Отже, за означенням
 (5) або
(5) або 
 (6).
(6).
На практиці зручною для обчислень є така формула:
 (7), тобто
(7), тобто  .
.
Це пояснюється тим, що  дуже часто обчислюється наближено, що приводить до нагромадження помилок заокруглень при обчисленні
дуже часто обчислюється наближено, що приводить до нагромадження помилок заокруглень при обчисленні  за формулою (5). Небезпека значних помилок заокруглень зростає із збільшенням обсягу вибірки.
за формулою (5). Небезпека значних помилок заокруглень зростає із збільшенням обсягу вибірки.
Оскільки  має одиниці вимірювання ознаки
має одиниці вимірювання ознаки  , то розглядають ще одну числову характеристику.
, то розглядають ще одну числову характеристику.
Середнім квадратичним відхиленням (або статистичною похибкою) називається корінь квадратичний з статистичної дисперсії.
На практиці, коли обсяг вибірки n < 30, використовують виправлену статистичну дисперсію  та виправлене середнє квадратичне відхилення:
та виправлене середнє квадратичне відхилення:
 і
і 
Формули для обчислення  мають вигляд:
мають вигляд:
а) для згрупованих даних

 (8) або
(8) або 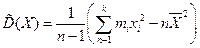 (9)
(9)
б) для незгрупованих даних
 ,
,  .
.
Необхідність таких змін пов’язана з властивостями точкових оцінок для параметрів теоретичного розподілу (див.лаб.роб.3).
Для кількісної оцінки ступеня відхилення експериментальної кривої розподілу від теоретичної кривої розподілу використовують асиметрію і ексцес, що обчислюється за формулами:
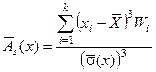

Якщо розподіл симетричний, то  .
.
Якщо  ,то вершина експериментальної кривої зміщена вліво якщо
,то вершина експериментальної кривої зміщена вліво якщо  , то відповідно – вправо.
, то відповідно – вправо.
Якщо 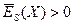 , то вершина експериментальної кривої піднята (крива крута), якщо
, то вершина експериментальної кривої піднята (крива крута), якщо  , то вершина такої кривої опущена (крива полога).
, то вершина такої кривої опущена (крива полога).
При порівнянні між собою ступенів варіації ознак, виражених у різних одиницях вимірювання, виникають певні труднощі. Для того щоб відповісти на запитання яка з ознак варіює сильніше тільки на основі порівняння стандартних відхилень неможливо. Потрібно співставити стандартне відхилення з середньою арифметичною цих ознак. Для цього вводиться коефіцієнт варіації,  який визначається за формулою:
який визначається за формулою:

Цей коефіцієнт є відносною мірою розсіювання ознаки. Він використовується і як показник однорідності вибіркових спостережень. Вважається, що якщо  , то вибірку можна вважати однорідною, тобто отриманою з однієї генеральної сукупності. На практиці
, то вибірку можна вважати однорідною, тобто отриманою з однієї генеральної сукупності. На практиці 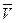 використовують для порівняння вибірок з однотипних генеральних сукупностей.
використовують для порівняння вибірок з однотипних генеральних сукупностей.
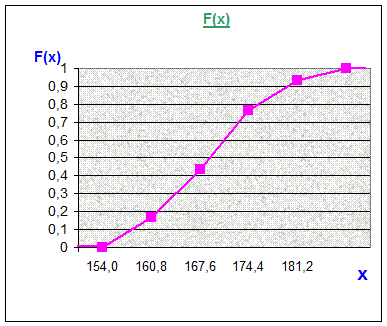
Завдання. Знайти статистичні функції розподілу для дискретної ознаки (розмір взуття учня) і неперервної ознаки (зріст учня), використавши частотні таблиці цих ознак, одержані в лаб.роб.№1 (див. крок 3 табл.4 та крок 5 табл.5). Побудувати графіки цих функцій (кумулятативні криві).
Хід роботи
1. Знайдіть статистичну функцію розподілу частот дискретної випадкової величини “розмір взуття” і побудуйте її кумулятативну криву. Для цього використайте табл.4 (крок 3 лаб.роб.№1).

2. Знайдіть статистичну функцію розподілу частот неперервної випадкової величини “зріст” і побудуйте її кумулятативну криву. Для цього використайте табл.4’ (крок 3 лаб.роб.№1).
|
|
|
Завдання. Обчислити числові характеристики дискретної ознаки – розмір взуття учня, використавши частотну таблицю цієї ознаки, що одержана при використанні лабораторної роботи 1. (див. крок 3 табл.4).
Хід роботи
1. Знайдіть вибіркове середнє 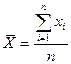 за допомогою статистичної функції УРЕЗСРЕДНЕЕ, де аргументами є діапазон комірок (табл.1 лаб.роб.№1) і 0 в якості долі.
за допомогою статистичної функції УРЕЗСРЕДНЕЕ, де аргументами є діапазон комірок (табл.1 лаб.роб.№1) і 0 в якості долі.
2. Знайдіть вибіркову (зміщену) дисперсію, використовуючи функцію ДИСП (аргументи хі – відповідний діапазон комірок табл.1 лаб.роб.№1).
3. Знайдіть вибіркове (зміщене) середнє квадратичне відхилення за формулою 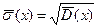 (=КОРЕНЬ(ім’я комірки зі значенням
(=КОРЕНЬ(ім’я комірки зі значенням  )) або за допомогою статистичної функції СТАНДОТКЛОН.
)) або за допомогою статистичної функції СТАНДОТКЛОН.
4. Знайдіть виправлену вибіркову (незміщену) дисперсію, використовуючи формулу 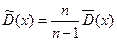 .
.
5. Знайдіть виправлене вибіркове (незміщене) середнє квадратичне відхилення за формулою 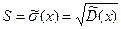 .
.
6. Знайдіть варіаційний розмах 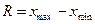 , використавши дані табл.2.
, використавши дані табл.2.
7. Знайдіть моду, використавши функцію МОДА.
8. Знайдіть медіану, використавши функцію МЕДИАНА, де аргументами є значення Хі табл.3.
9. Знайдіть асиметрію, використавши функцію СКОС.
10. Знайдіть ексцес, використавши однойменну статистичну функцію.
11. Обчисліть коефіцієнт варіації, використавши знайдені значення
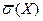 і
і  .
.
Зразок оформлення звіту до лабораторної роботи
| Обчислення числових характеристик | |||||||||||
| Статистичне (вибіркове) середнє | 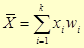 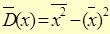 |
||||||||||
| 38,87 | 38,87 | ||||||||||
| Статистична (вибіркова) дисперсія | 5,22 | 5,22 | |||||||||
| Статистичне середнє | 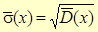 |
||||||||||
| квадратичне відхилення | 2,28 | або | 2,29 | ||||||||
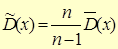 |
|||||||||||
| Виправлена статистична дисперсія | 5,40 | ||||||||||
| виправлене середнє |  |
2,32 | |||||||||
| квадратичне відхилення | |||||||||||
 |
|||||||||||
| Варіаційний розмах | R = | 7,00 | |||||||||
| Мода | МОДА(х)= | 37,00 | |||||||||
| Медіана | МЕДИАНА(Х)= | 39,50 | |||||||||
| Асиметрія | СКОС(Х)= | 0,41 | |||||||||
| Ексцес | ЭКСЦЕСС(Х)= | -1,20 | |||||||||
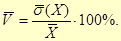 |
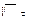 |
||||||||||
| Коефіцієнт варіації | 5,88% | ||||||||||
|
|
|
Знаходження точкових та інтервальних оцінок параметрів генеральної сукупності за вибіркою (неперервна ознака).
Побудова статистичної кривої розподілу.
Мета: Навчитися обчислювати числові характеристики неперервної ознаки; будувати статистичні криві розподілу і порівнювати їх з відповідними теоретичними кривими, зокрема, з нормальною кривою; оволодіти методами побудови надійних інтервалів для оцінок параметрів нормального розподілу.
1. Числові характеристики вибірки (для неперервної ознаки).
Нехай вибірка для неперервної ознаки 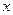 представлена інтервальною частотною таблицею.
представлена інтервальною частотною таблицею.
Формули числових характеристик для дискретної ознаки використовуються і для знаходження числових характеристик неперервної ознаки, якщо замість інтервальної частотної таблиці буде побудована частотна таблиця. Для цього потрібно замінити інтервали їх представниками, рівними середині іншого інтервалу:  . Одержується послідовність рівновіддалених варіант, частоти яких дорівнюють відповідним частотам інтервалів. Ця інформація записується у вигляді частотної таблиці:
. Одержується послідовність рівновіддалених варіант, частоти яких дорівнюють відповідним частотам інтервалів. Ця інформація записується у вигляді частотної таблиці:
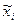 |
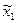 |
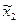 |
... |  |
 |
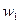 |
 |
... |  |
Таку частотну таблицю використовують для побудови полігону частот: першими координатами точок ламаної лінії є середини інтервалів, а другими - відносні (абсолютні) частоти, що відповідають даним інтервалам. Таку лінію ще називають частотною ламаною або статистичною (експериментальною) кривою розподілу, так як вона показує розподіл вивчаємої ознаки по окремих інтервалах:
 |

 y
y
 |
|||
 |
|||
 wk-1
wk-1







 w3
w3



 w2
w2
w1





 wk
wk
 |
x1 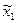 x2
x2  x3
x3 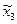 x4 xk-1
x4 xk-1 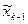 xk
xk  xk+1 xi
xk+1 xi
При збільшенні числа спостережень (вимірювань) і зменшенні інтервального проміжку крива розподілу намагається стати плавною кривою. Криві розподілу можуть мати різні форми – криві з вершинами, зсунутими вправо або вліво; криві з піднятими або сплющеними вершинами, багато вершинні криві. Симетричні криві розподілу називають кривими нормального розподілу.
Статистичне оцінювання параметрів розподілу
(оцінка параметрів генеральної сукупності за вибіркою)
а) Точкове оцінювання параметрів розподілу.
Нехай потрібно підібрати деякий розподіл для досліджуваної випадкової величини 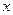 за вибіркою
за вибіркою  . Виходячи з аналізу вибірки (наприклад, по виду гістограми чи полігону відносних частот), можна вибрати певний розподіл (нормальний, рівномірний, біноміальний тощо).
. Виходячи з аналізу вибірки (наприклад, по виду гістограми чи полігону відносних частот), можна вибрати певний розподіл (нормальний, рівномірний, біноміальний тощо).
Після того, як вид розподілу випадкової величини вибрано (він, зрозуміло, містить невідомі параметри), переходять до оцінки параметрів гіпотетичного (теоретичного) розподілу за даними вибірки. Так, наприклад, для нормального розподілу це параметри а і б. Розв’язання питання “про найкращу” оцінку невідомого параметру розподілу і складає теорію статистичного оцінювання.
Кожна числова характеристика вибірки – це реалізація випадкової величини, яка від вибірки до вибірки може приймати різні значення, а значить сама є випадковою величиною. Таку випадкову величину називають статистикою (статистичною оцінкою) і позначають 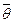 . Отже,
. Отже, 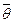 - статистична оцінка параметра
- статистична оцінка параметра  теоретичного розподілу.
теоретичного розподілу.
Оцінки бувають точкові і інтервальні.
Оцінка називається точковою, якщо вона визначається одним числом.
В ролі точкових оцінок використовують числові характеристики вибірки. Наприклад,  - оцінка математичного сподівання
- оцінка математичного сподівання 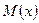 генеральної сукупності. В принципі для невідомого параметра
генеральної сукупності. В принципі для невідомого параметра  може існувати декілька числових характеристик вибірки, які цілком підходять для того, щоб бути оцінкою. Наприклад,
може існувати декілька числових характеристик вибірки, які цілком підходять для того, щоб бути оцінкою. Наприклад,  ,
, 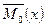 ,
,  можуть бути оцінками для
можуть бути оцінками для 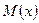 , а
, а  і
і  - оцінками для дисперсії
- оцінками для дисперсії  .
.
Щоб вирішити, яка з статистик є найкращою, потрібно визначити деякі бажані властивості таких оцінок.
Оцінка 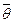 називається незміщеною (незсуненою) оцінкою параметра
називається незміщеною (незсуненою) оцінкою параметра  , якщо при довільному обсязі вибірки математичне сподівання оцінки
, якщо при довільному обсязі вибірки математичне сподівання оцінки 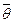 дорівнює оцінюваному параметру
дорівнює оцінюваному параметру  , тобто
, тобто 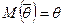 , де
, де  .
.
Незсуненість оцінки означає, що при використанні цієї оцінки в одних випадках завищується шуканий параметр статистичної сукупності, в інших – занижується. Але в середньому, як кажуть, ми будемо “попадати в точку”. Отже, вимога незсуненості оцінки гарантує від одержання систематичних помилок (помилок одного знаку).
Якщо існує більше однієї незсуненої оцінки, то вибирають більш ефективну оцінку.
Оцінка  називається ефективною оцінкою параметра
називається ефективною оцінкою параметра  , якщо при заданому обсязі вибірки вона має найменшу дисперсію, тобто
, якщо при заданому обсязі вибірки вона має найменшу дисперсію, тобто  .
.
При використанні тієї чи іншої оцінки бажано, щоб точність оцінки 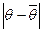 збільшувалась із збільшенням об’єму вибірки. Гранична точність буде досягнута тоді, коли значення оцінки співпаде із значенням параметра при необмеженому збільшенні об’єму вибірки. Такі оцінки називаються спроможними.
збільшувалась із збільшенням об’єму вибірки. Гранична точність буде досягнута тоді, коли значення оцінки співпаде із значенням параметра при необмеженому збільшенні об’єму вибірки. Такі оцінки називаються спроможними.
Оцінка 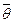 називається спроможною (консистентною) оцінкою параметра
називається спроможною (консистентною) оцінкою параметра  , якщо при
, якщо при 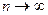 вона збігається за ймовірністю до оцінюваного параметра
вона збігається за ймовірністю до оцінюваного параметра  , тобто
, тобто
Зауваження. При виборі оцінок слід приймати до уваги наведені властивості і враховувати відносну простоту обчислень. Іноді вибирається неефективна оцінка тільки тому, що її обчислення набагато простіше, ніж обчислення ефективної оцінки. Наприклад, для контролю якості продукції мірою розсіювання статистичної сукупності часто служить варіаційний розмах R, який використовується замість більш складної і ефективної оцінки- статистичного стандартного відхилення 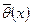 . Можна показати, що оцінка
. Можна показати, що оцінка  є незміщеною, не є ефективною, але є спроможною для дисперсії
є незміщеною, не є ефективною, але є спроможною для дисперсії  . Щоб статистична дисперсія, як оцінка, стала незміщеною, вводять поняття виправленої статистичної дисперсії
. Щоб статистична дисперсія, як оцінка, стала незміщеною, вводять поняття виправленої статистичної дисперсії  , яка обчислюється за формулою:
, яка обчислюється за формулою: 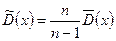 , де
, де 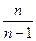 - поправка Бесселя.
- поправка Бесселя.
Зауваження. Поправка Бесселя при малих значеннях 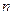 значно відрізняється від 1. Тому при
значно відрізняється від 1. Тому при  користуються виправленою статистичною дисперсією. При
користуються виправленою статистичною дисперсією. При  практично немає різниці між використанням
практично немає різниці між використанням  і
і  .
.
 2017-10-25
2017-10-25 4234
4234








