Парный регрессионный анализ

Лекция 3

1. Корреляционная зависимость
2. Парная регрессия
3. Парная линейная регрессия. Метод наименьших квадратов
4. Свойства оценок МНК.
5. Сравнение свойств истинных и оцененных зависимостей

-1-

Модели корреляционно-регрессионного анализа представляют собой основной математический инструмент эконометрики. В естественных науках большинство зависимостей между переменными носят функциональный характер. В экономике основные зависимости между переменными носят статистический характер. Это означает, что каждому значению одной переменной может соответствовать множество значений других переменных. Если рассматривается зависимость между одной эндогенной переменной (y) и одной экзогенной переменной (x), то такая зависимость называется парной (корреляционной) зависимостью.

Статистический анализ зависимости обусловлен тем, что всегда существуют неконтролируемые или неучтенные факторы, а так же тем, что существуют ошибки измерения и ошибки выборки. Такие статистические зависимости называют «вероятностными», «стохастическими», «корреляционными».

Примеры статистических зависимостей:

· Зависимость между потреблением y и доходом и составом семьи (x1 x2)

· Зависимость между спросом и ценой (y и х)

· Зависимость между урожайностью почвы (y) и количеством внесенных удобрений (x)

· Зависимость между объемом продаж (у) и вложениями в рекламу (х)

· И множество других зависимостей

В силу неоднозначности статистической зависимости X и Y представляет интерес усредненная по X схема зависимости. То есть измерение условного математического ожидания переменной Y в зависимости от значения x.

Условное математическое ожидание Y обозначается:

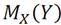
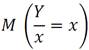
Условным математическим ожиданием переменной из двумерной случайной величины (X:Y) называется математическое ожидание, вычисленное при условии что другая переменная приняла определенное значение.

Корреляционной зависимостью между двумя переменными называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой. Корреляционная зависимость обладает следующими особенностями.

1. Эта зависимость проявляется во множестве наблюдений.
2. Эта зависимость является частичной (не полной).

Исходные данные могут быть представлены в виде таблиц, графиков, формул и т.д.

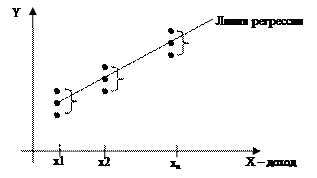
Исходные статистические данные, отраженные на координатной плоскости называются корреляционным полем.

Корреляционная зависимость математически может быть представлена виде:

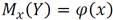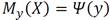или (*1)

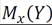- условное математическое ожидание y

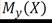- условное математическое ожидание x

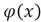и 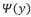- модельная функция регрессии

Эта формула называется модельным уравнением регрессии.

График модельной функции регрессии называется модельной линией регрессии или просто линией регрессии. Описать корреляционную зависимость означает построить уравнение регрессии.

Уравнение регрессии – теоретическое уравнение связи – это функциональная зависимость, которая наилучшим образом аппроксимирует исходную статистическую зависимость.

Генеральная совокупность исходных данных может быть оценена по выборке xi yi размером n (i=1,n). То есть строится оцененное выборочное уравнение регрессии.

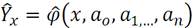
Его график – выборочная линия регрессии.

-2-

Парная регрессия

Виды моделей парной регрессии:

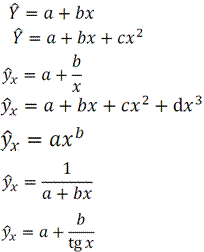1.

2.

3.

4.

5.

6.

7.

-3-

Парная линейная регрессия. Модель парной линейной регрессии имеет вид:

()

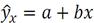
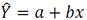Или полный вид:

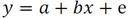(*3)

это выборочная линейная регрессия.

Для генеральной совокупности парная линейная регрессия имеет вид:

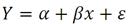
a – есть оценка по выборке параметра α

b – оценка по выборке параметра β.

e – оценка по выборке параметра ε.

Построить выборочное уравнение регрессии, значит найти все его параметры (a и b). Построение уравнения регрессии основывается на методе наименьших квадратов.

Его суть:

Сумма квадратов отклонений фактических значений показателя от теоретических должна быть минимальной. Математически:

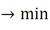
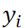- исходное значение экономического показателя.

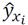- значение экономического показателя на уравнение регрессии теоретические

Метод наименьших квадратов для парной линейной регрессии будет иметь вид:

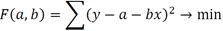
Решая эту модель, найдем оценки параметров a и b. И получим модель парной линейной регрессии вида:

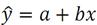
b – называется коэффициентом регрессии, он показывает на сколько единиц в среднем изменится y при изменении x на одну единицу.

-4-

Чтобы оценки a и b по выборке можно было применить к генеральной совокупности должны быть сделаны следующие предположения о случайных отклонениях ε_i:

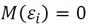
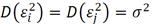
1. ε_i случайны
2. Имеют нулевое математическое ожидание
3. Имеют равную дисперсию.
4. ε_i - независимы между собой.

Если выполняются эти предпосылки, то оценки a и b обладают следующими свойствами:

1. Не смещенность.
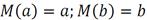
2. Состоятельность. При увеличении числа наблюдений a близко к α, b близко к β.

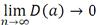
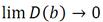
1. Эффективность. Оценки имеют наименьшую дисперсию среди всех других линейных оценок. (BLUE – Best Linear Unbiased Estimators)

Линейная регрессия строится по методу наименьших квадратов. Рассмотрим метод наименьших квадратов для парной линейной регрессии. Далее суммирование по всем наблюдениям.

Для решения указанной модели выполним необходимое условие минимума функции F(a,b) и достаточное условие. Найдем частные производные и приравняем их к нулю. (**1)

Преобразуем систему уравнений: (**2)

n – число наблюдений.

Это система нормальных уравнений (5) для нахождения параметров a и b модели парной линейной регрессии.

Решая систему любым известным методом найдем оценки параметров a и b. Решить систему можно:

1. По методу определителей) (**3)

2. a и b можно найти по формулам(**4)

Существует правило «автоматизма» для построения Системы Нормальных Уравнений (СНУ). Чтобы построить i-ое уравнение системы надо исходное уравнение умножить на коэффициент при i-м неизвестном, просуммировав обе части уравнения и заменив (**5)

-5-

Сравнение истинных и оцененных зависимостей

(**6)

В реальности можно оценить зависимость между расходами и доходами только по выборке.

Выборочная модель имеет вид (**7)