Таблица 2.1
Индивидуальное потребление и личные доходы (США, 1954-1965 гг.)
| Год | Индивидуальное потребление, млрд. долл. | Личные доходы, млрд. долл. |
Заметим, что исходные данные должны быть выражены величинами примерно одного порядка. Вычисления удобно организовать, как показано в таблице 2.2. Сначала рассчитываются 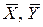 , затем x i, y i. Результаты заносятся в столбцы 3 и 4. Далее определяются x i2, x i y i и заносятся в 5 и 6 столбцы таблицы 2.2. По формулам (2.8) получим искомые значения параметров
, затем x i, y i. Результаты заносятся в столбцы 3 и 4. Далее определяются x i2, x i y i и заносятся в 5 и 6 столбцы таблицы 2.2. По формулам (2.8) получим искомые значения параметров 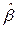 =43145/46510=0,9276;
=43145/46510=0,9276; 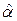 =321,75-0,9276.350=-2,91.
=321,75-0,9276.350=-2,91.
Оцененное уравнение регрессии запишется в виде 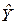 =-2,91+0,9276 X.
=-2,91+0,9276 X.
Следующая важная проблема состоит в том, чтобы определить, насколько "хороши" полученные оценки и уравнение регрессии. Этот вопрос рассматривается по следующим стадиям исследования: квалифицирование (выяснение условий применимости результатов), определение качества оценок, проверка выполнения допущений метода наименьших квадратов.
Относительно квалифицирования уравнения 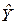 =-2,91+0,9276 X. Оно выражает, конечно, достаточно сильное утверждение. Применять это уравнение для прогнозирования следует очень осторожно. Дело в том, что, даже отвлекаясь от многих факторов, влияющих на потребление, и от систематического изменения дохода по мере варьирования потребления, мы не располагаем достаточно представительной выборкой.
=-2,91+0,9276 X. Оно выражает, конечно, достаточно сильное утверждение. Применять это уравнение для прогнозирования следует очень осторожно. Дело в том, что, даже отвлекаясь от многих факторов, влияющих на потребление, и от систематического изменения дохода по мере варьирования потребления, мы не располагаем достаточно представительной выборкой.
Таблица 2.2
Рабочая таблица расчетов (по данным табл. 2.1)
| Год | X | Y | x | y | x 2 | xy | 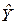
| ei |
| -93 | -85,75 | 7974,75 | 235,48 | 0,52 | ||||
| -75 | -67,75 | 5081,25 | 252,18 | 1,82 | ||||
| -57 | -54,75 | 3120,75 | 268,88 | -1,88 | ||||
| -41 | -40,75 | 1670,75 | 283,72 | -2,72 | ||||
| -31 | -31,75 | 984,25 | 292,99 | -2,99 | ||||
| -13 | -10,75 | 139,75 | 309,69 | 1,31 | ||||
| 3,25 | 321,75 | 3,25 | ||||||
| 13,25 | 185,5 | 334,74 | 0,26 | |||||
| 33,25 | 1163,75 | 354,22 | 0,78 | |||||
| 53,25 | 2928,75 | 372,77 | 2,23 | |||||
| 79,25 | 6894,75 | 402,45 | -1,45 | |||||
| 109,25 | 13000,75 | 432,13 | -1,13 | |||||
| å | 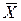 =350,00 =350,00
| 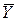 =321,75 =321,75
| 0,00 | 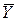 =321,75 =321,75
| 0,00 |
Полученное уравнение 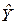 =-2,91+0,9276 X можно использовать для расчета точечного прогноза, в том числе и на ретроспективу. Подставляя последовательно значения X из второго столбца табл. 2.2 в уравнение
=-2,91+0,9276 X можно использовать для расчета точечного прогноза, в том числе и на ретроспективу. Подставляя последовательно значения X из второго столбца табл. 2.2 в уравнение 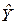 =-2,91+0,9276 X, получим предпоследний столбец табл. 2.2 для прогнозных значений
=-2,91+0,9276 X, получим предпоследний столбец табл. 2.2 для прогнозных значений 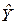 . Ошибка прогноза вычисляется по формуле e i= Y i -
. Ошибка прогноза вычисляется по формуле e i= Y i - 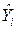 и дана в последнем столбце рабочей таблицы.
и дана в последнем столбце рабочей таблицы.
Заметим, что ошибка прогноза e i фактически является оценкой значений u i. График ошибки e i представлен на рис. 2.2. Следует отметить факт равенства нулю суммы S e i=0, что согласуется с первым ограничением модели парной регрессии - E ui =0, i =1,…, n. Ñ
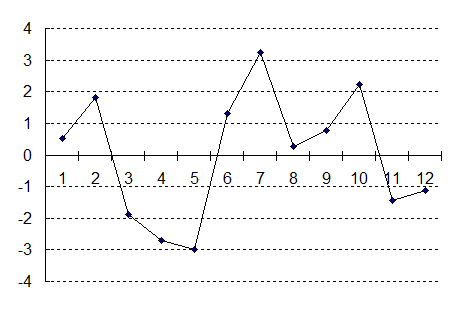
Рис. 2.2. График ошибки прогноза
В модели (2.2) функция f может быть и нелинейной. Причем выделяют два класса нелинейных регрессий:
q регрессии, нелинейные относительно включенной объясняющей переменной, но линейные по параметрам, например полиномы разных степеней - Yi = a 0 + a 1 Xi + a 2 Xi 2+ ui, i =1,…, n или гипербола - Yi = a 0 + a 1/ Xi + u i, i =1,…, n;
q регрессии нелинейные по оцениваемым параметрам, например степенная функция - Yi = a 0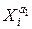 ui, i =1,…, n, или показательная функция - Yi =
ui, i =1,…, n, или показательная функция - Yi =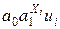 , i =1,…, n.
, i =1,…, n.
В первом случае МНК применяется так же, как и в линейной регрессии, поскольку после замены, например, в квадратичной параболе Yi = a 0 + a 1 Xi + a 2 Xi 2+ ui переменной Xi 2 на X 1i: Xi 2= X 1i, получаем линейное уравнение регрессии Yi = a 0 + a 1 Xi + a 2 X 1i+ ui, i =1,…, n.
Во втором случае в зависимости от вида функции возможно применение линеаризующих преобразований, приводящих функцию к виду линейной. Например, для степенной функции Yi = a 0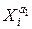 ui после логарифмирования получаем
ui после логарифмирования получаем 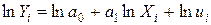 линейную функцию в логарифмах и применяем МНК.
линейную функцию в логарифмах и применяем МНК.
Однако для, например, модели Yi = a 0+ a 2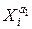 + ui линеаризующее преобразование отсутствует, и приходится применять другие способы оценивания (например, нелинейный МНК).
+ ui линеаризующее преобразование отсутствует, и приходится применять другие способы оценивания (например, нелинейный МНК).
Для трактовки линейной связи между двумя переменными акцентируют внимание на коэффициенте корреляции.
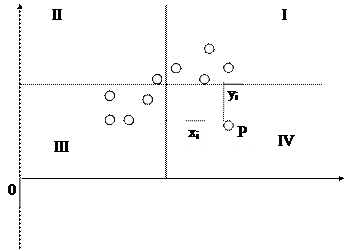
Пусть имеется выборка наблюдений (X i, Y i), i =1,..., n, которая представлена на диаграмме рассеяния, именуемой также полем корреляции (рис. 2.3).
Y
X
Рис. 2.3. Диаграмма рассеяния
Разобьем диаграмму на четыре квадранта так, что для любой точки P (X i, Y i) будут определены отклонения 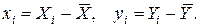
Ясно, что для всех точек I квадранта x i y i>0; для всех точек II квадранта x i y i<0; для всех точек III квадранта x i y i>0; для всех точек IV квадранта x i y i<0. Следовательно, величина å x i y i может служить мерой зависимости между переменными X и Y. Если большая часть точек лежит в первом и третьем квадрантах, то å x i y i>0 и зависимость положительная, если большая часть точек лежит во втором и четвертом квадрантах, то å x i y i<0 и зависимость отрицательная. Наконец, если точки рассеиваются по всем четырем квадрантам å x i y i близка к нулю и между X и Y связи нет.
Указанная мера зависимости изменяется при выборе единиц измерения переменных X и Y. Выразив å x i y i в единицах среднеквадратических отклонений, получим после усреднения выборочный коэффициент корреляции:
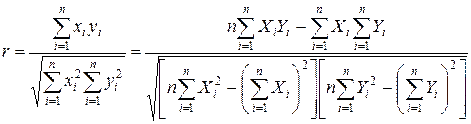 (2.9)
(2.9)
Из последнего выражения можно после преобразований получить следующую формулу для квадрата коэффициента корреляции:
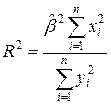 или
или
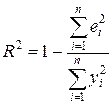 (2.10)
(2.10)
Квадрат коэффициента корреляции называется коэффициентом детерминации. Согласно (2.10) значение коэффициента детерминации не может быть больше единицы, причем это максимальное значение будет достигнуто при 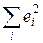 =0, т.е. когда все точки диаграммы рассеяния лежат в точности на прямой. Следовательно, значения коэффициента корреляции лежат в числовом промежутке от -1 до +1.
=0, т.е. когда все точки диаграммы рассеяния лежат в точности на прямой. Следовательно, значения коэффициента корреляции лежат в числовом промежутке от -1 до +1.
Кроме того, из (2.10) следует, что коэффициент детерминации равен доле дисперсии Y (знаменатель формулы), объясненной линейной зависимостью от X (числитель формулы). Это обстоятельство позволяет использовать R 2 как обобщенную меру "качества" статистического подбора модели (2.6). Чем лучше регрессия соответствует наблюдениям, тем меньше 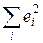 и тем ближе R 2 к 1, и наоборот, чем "хуже" подгонка линии регрессии к данным, тем ближе значение R 2 к 0.
и тем ближе R 2 к 1, и наоборот, чем "хуже" подгонка линии регрессии к данным, тем ближе значение R 2 к 0.
Поскольку коэффициент корреляции симметричен относительно X и Y, то есть r XY= r YX, то можно говорить о корреляции как о мере взаимозависимости переменных. Однако из того, что значения этого коэффициента близки по модулю к единице, нельзя сделать ни один из следующих выводов: Y является причиной X; X является причиной Y; X и Y совместно зависят от какой-то третьей переменной. Величина r ничего не говорит о причинно-следственных связях. Эти вопросы должны решаться, исходя из содержательного анализа задачи. Следует избегать и так называемых ложных корреляций, т.е. нельзя пытаться связать явления, между которыми отсутствуют реальные причинно-следственные связи. Например, корреляция между успехами местной футбольной команды и индексом Доу-Джонса. Классическим является пример ложной корреляции, приведенный в начале ХХ века известным российским статистиком А.А. Чупровым: если в качестве независимой переменной взять число пожарных команд в городе, а в качестве зависимой переменной – сумму убытков от пожаров за год, то между ними есть прямая корреляционная зависимость, т.е. чем больше пожарных команд, тем больше сумма убытков. На самом деле здесь нет причинно-следственной связи, а есть лишь следствия общей причины – величины города.
Проверка гипотезы о значимости выборочного коэффициента корреляции эквивалентна проверке гипотезы о b =0 (см. ниже) и, следовательно, равносильна проверке основной гипотезы об отсутствии линейной связи между Y и X. Вычисляя значение t -статистики
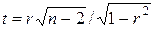 ,
,
вывод о значимости r делается при | t |> t e, где t e - соответствующее табличное значение t -распределения с (n -2) степенями свободы и уровнем значимости e.
Пример. Вычислим коэффициент корреляции и проверим его значимость для нашего примера табл. 2.1.
По (2.9) r =43145/(46510×40068,25)0,5=0,9994. R 2=0,998. Значение t -статистики t =0,9994×[10/(1-0,998)]0,5=70,67. Поскольку t 0,05;10=2,228, то t > t 0,05;10 и коэффициент корреляции значим. Следовательно, можно считать, что линейная связь между переменными Y и X в примере существует. Ñ
Если между переменными имеет место нелинейная зависимость, то коэффициент корреляции теряет смысл как характеристика степени тесноты связи. В этом случае используется наряду с расчетом коэффициента детерминации расчет корреляционного отношения.
Предположим, что выборочные данные могут быть сгруппированы по оси объясняющей переменной X. Обозначим s – число интервалов группирования, 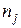 (j =1,…, s) – число выборочных точек, попавших в j -й интервал группирования,
(j =1,…, s) – число выборочных точек, попавших в j -й интервал группирования, 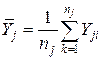 - среднее значение ординат точек, попавших в j -й интервал группирования,
- среднее значение ординат точек, попавших в j -й интервал группирования, 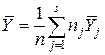 - общее среднее по выборке. С учетом формул для оценок выборочных дисперсий среднего значения Y внутри интервалов группирования
- общее среднее по выборке. С учетом формул для оценок выборочных дисперсий среднего значения Y внутри интервалов группирования 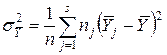 и суммарной дисперсии результатов наблюдения
и суммарной дисперсии результатов наблюдения 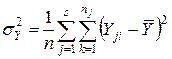 получим:
получим:
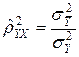 . (2.11)
. (2.11)
Величину 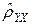 в (2.11) называют корреляционным отношением зависимой переменной Y по независимой переменной X. Его вычисление не предполагает каких-либо допущений о виде функции регрессии.
в (2.11) называют корреляционным отношением зависимой переменной Y по независимой переменной X. Его вычисление не предполагает каких-либо допущений о виде функции регрессии.
Величина 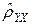 по определению неотрицательная и не превышает единицы, причем
по определению неотрицательная и не превышает единицы, причем 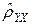 =1 свидетельствует о наличии функциональной связи между переменными Y и X. Если указанные переменные не коррелированны друг с другом, то
=1 свидетельствует о наличии функциональной связи между переменными Y и X. Если указанные переменные не коррелированны друг с другом, то 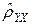 =0.
=0.
Можно показать, что 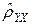 не может быть меньше величины коэффициента корреляции r (формула (2.9)) и в случае линейной связи эти величины совпадают.
не может быть меньше величины коэффициента корреляции r (формула (2.9)) и в случае линейной связи эти величины совпадают.
Это позволяет использовать величину разности 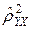 – R 2 в качестве меры отклонения регрессионной зависимости от линейного вида.
– R 2 в качестве меры отклонения регрессионной зависимости от линейного вида.
 2014-02-01
2014-02-01 730
730








