Во многих экономических, управленческих и иных задачах рассматриваются независимые многократно повторяемые испытания. Каждое такое испытание приводит к одному из двух возможных исходов, называемых часто успехом и неудачей, и вероятность успеха р не меняется от одного опыта к другому. Например, если монета является геометрически правильной, то р =0,5 для любого исхода. Вероятность появления ровно x успешных исходов в n независимых испытаниях определяется распределением Бернулли или биноминальным распределением.
В Excel биноминальное распределение использовано в функциях БИНОМРАСП, ОТРБИНОМРАСП, КРИТБИНОМ.
Рассмотрим некоторые примеры применения биноминального распределения.
Пример 2.7 Предприятие производит электрические лампочки. Отдел качества из каждой партии случайным образом выбирает 100 ламп. Партия принимается, если партия содержит не более 3 дефектных ламп. Какова вероятность принятия партии, если в процессе производства в среднем 0,5% ламп дефектны? Эту задачу применительно к статистике можно сформулировать так: какова вероятность появления не более x =3 успешных исходов в n =100 независимых испытаниях Бернулли, если вероятность успешного исхода при одном испытании р =0,005.
Используем функцию БИНОМРАСП, которая имеет следующий синтаксис:
БИНОМРАСП(число_успехов; число_испытаний; вероятность_успеха; интегральная),
где число_успехов – количество успешных испытаний;
число_испытаний – число независимых испытаний;
вероятность_успеха – вероятность успеха каждого (одного) испытания;
интегральная – логическое значение принимается равным 1 или 0; если интегральная=1, то определяется вероятность того, что число успешных испытаний (число _успехов) не более заданного; если интегральная=0, то определяется вероятность того, что число успешных испытаний в точности соответствует заданному.
Использование функции будет следующим БИНОМРАСП(3;100;0,005,1), результат которой есть значение 0,9983. Т.е. вероятность принятия партии ламп в выборке из 100 штук при условии, что в партии окажется не более 3 неисправных ламп составляет 0,9983, что близко к 1.
Функция КРИТБИНОМ является обратной по отношению к БИНОМРАСП. Используется в задачах, связанных с контролем качества продукции. Синтаксис функции
КРИТБИНОМ(число_испытаний; вероятность_успеха; альфа),
где альфа – значение критерия.
Изменим исходные данные примера 2.7. Определим наибольшее допустимое число дефектных ламп x в выборке, при котором вероятность принятия партии составит а)0,9; б)0,95; в)0,99. При этом количество дефектных ламп в процессе производства составляет в среднем 0,5%.
Использование функции КРИТБИНОМ будет таким:
а) КРИТБИНОМ(100;0,005;0,90),
б) КРИТБИНОМ(100;0,005;0,95),
в) КРИТБИНОМ(100;0,005;0,99).
В результате получены следующие соответствующие количества дефектных ламп в выборке
а) 1,
б) 2,
в) 3.
Из результатов видно, что если количество дефектных ламп в выборке не более 1, вероятность принятия всей партии будет лежать в интервале от 0,90 до 0,95; не более 2 – в интервале от 0,95 до 0,99; не более 3 – в интервале от 0,99 до некоторого значения, которое определяется отдельно.
Точное значение вероятности принятия партии для конкретного количества дефектных ламп в выборке можно определить с помощью функции БИНОМРАСП.
3 Режим "Описательная статистика"
В Excel есть режим "Описательная статистика", которая служит для генерации одномерного статистического отчета по основным показателям положения, разброса и асимметрии выборочной совокупности. Для того, чтобы использовать этот режим необходимо установить надстройку "Пакет анализа" через действие
Сервис/Надстройка…
В открывшемся окне в списке надстроек найти и отметить "Пакет анализа", далее действовать по инструкциям, выдаваемым компьютером. После установки "Пакета анализа" в меню "Сервис" появится новое действие "Анализ данных", которым можно будет пользоваться. Выполнив действие Сервис/Анализ данных…, появится диалоговое окно, где выбираем инструмент анализа "Описательная статистика" и, щелкнув кнопку ОК, на экране появится следующее диалоговое окно

Рис.3.1
Поле "Входной интервал" – вводится ссылка на ячейки, которые содержат анализируемые данные.
Флажок "Метки…" устанавливается в активное состояние, если первая строка (или столбец) во входном диапазоне содержит заголовки.
Если активизировать переключатель на "Выходной интервал", то слева в поле необходимо будет ввести ссылку на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона определяется автоматически.
В положении "Новый рабочий лист" открывается новый рабочий лист, куда, начиная с ячейки А1 вставляются результаты анализа.
В положении "Новая рабочая книга" открывается новая рабочая книга, куда на первый лист, начиная с ячейки А1, вставляются результаты анализа.
"Итоговая статистика" устанавливается в активное состояние, когда в выходном диапазоне необходимо получить следующие показатели описательной статистики:
- средняя арифметическая выборки ( );
);
- средняя ошибка выборки ( );
);
- медиана (Ме);
- мода (Мо);
- оценка стандартного отклонения по выборке (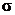 );
);
- оценка дисперсии по выборке (D);
- оценка эксцесса по выборке ( );
);
- оценка коэффициента асимметрии по выборке ( );
);
- размах вариации выборки (R);
- максимальный и минимальный элементы выборки;
- сумма элементов выборки;
- количество элементов выборки;
- k -й наибольший и k -й наименьший элементы выборки;
- предельная ошибка выборки ( ).
).
"Уровень надежности" – устанавливается в активное состояние, если в выходную таблицу необходимо включить строку для предельной ошибки выборки ( ) для установленного уровня надежности. В поле, напротив флажка вводится требуемое значение уровня надежности (например, уровня надежности 98% равносильно доверительной вероятности
) для установленного уровня надежности. В поле, напротив флажка вводится требуемое значение уровня надежности (например, уровня надежности 98% равносильно доверительной вероятности  =0,98 или уровню значимости
=0,98 или уровню значимости  =0,02).
=0,02).
" K -й наибольший" – устанавливается в активное состояние, если в выходную таблицу необходимо включить строку для k -го наибольшего (начиная с максимума  ) значения элемента выборки. В поле, напротив флажка вводится число k. Если k =1, то строка будет содержать максимальное значение элемента выборки.
) значения элемента выборки. В поле, напротив флажка вводится число k. Если k =1, то строка будет содержать максимальное значение элемента выборки.
" K -й наименьший" – аналогичен предыдущему, только отсчет идет от минимума  .
.
Пример 3.1. Стоимость набора из 25 продуктов питания по некоторым городам центрального региона России приведена в таблице 3.1. Необходимо рассчитать основные показатели описательной статистики и сделать соответствующие выводы.
Таблица 3.1
| Владимир | 1361,64 |
| Вологда | 1462,23 |
| Иваново | 1379,00 |
| Кострома | 1301,86 |
| Москва | 1840,86 |
| Н. Новгород | 1417,92 |
| Рязань | 1468,32 |
| Тверь | 1406,76 |
| Ярославль | 1466,40 |
Для решения задачи использован режим "Описательная статистика". Результат решения приведен в таблице 3.2, которая дополнена тем, что полученные цифры округлены до двух значащих цифр и для удобства пояснений к таблице добавлен средний столбец с обозначениями.
Таблица 3.2
| Столбец1 | ||
|
| ||
| Среднее | 
| 1456,11 |
| Стандартная ошибка | 
| 51,49 |
| Медиана | Ме | 1417,92 |
| Мода | Мо | #Н/Д |
| Стандартное отклонение | 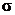
| 154,47 |
| Дисперсия выборки | D | 23860,36 |
| Эксцесс | 
| 6,06 |
| Асимметричность | 
| 2,26 |
| Интервал | R | 539,00 |
| Минимум | 1301,86 | |
| Максимум | 1840,86 | |
| Сумма | 13104,98 | |
| Счет | 9,00 | |
| Наибольший(1) | 1840,86 | |
| Наименьший(1) | 1301,86 | |
| Уровень надежности(95,0%) | 
| 118,73 |
Выводы по полученным результатам.
1. На основании проведенного выборочного обследования и рассчитанных по данной выборке показателей описательной статистики с уровнем надежности 95% можно предположить, что средняя стоимость набора из 25 продуктов питания в целом по всем городам центрального региона России находится в пределах от ( -
-  )=1337,38 до (
)=1337,38 до ( +
+  )=1574,84.
)=1574,84.
2. Коэффициент вариации

существенно меньше 40%, что свидетельствует о небольшом колебании признака в исследованной выборочной совокупности.
3. Надежность средней  в выборке подтверждается также ее незначительным отклонением от медианы
в выборке подтверждается также ее незначительным отклонением от медианы
 - Ме =38,19
- Ме =38,19
4. Степень асимметрии распределения определяет коэффициент асимметрии  =2,26. Коэффициент асимметрии может меняться от –3 до +3. Принято считать, что если
=2,26. Коэффициент асимметрии может меняться от –3 до +3. Принято считать, что если  >|0,5|, то асимметрия считается значительной; для
>|0,5|, то асимметрия считается значительной; для  <0,25 – незначительной. Если
<0,25 – незначительной. Если  >0, то имеется правосторонняя асимметрия (
>0, то имеется правосторонняя асимметрия ( > Мо). Следовательно, для данного примера имеем значительную правостороннюю асимметрию распределения.
> Мо). Следовательно, для данного примера имеем значительную правостороннюю асимметрию распределения.
5. Показатель эксцесса  =6,06. При симметричном распределении
=6,06. При симметричном распределении  =0. Если
=0. Если  >0, распределение является островершинным, если
>0, распределение является островершинным, если  <0 – плосковершинным. Для примера имеем эмпирическое распределение островершинным, что говорит о скоплении членов ряда около среднего
<0 – плосковершинным. Для примера имеем эмпирическое распределение островершинным, что говорит о скоплении членов ряда около среднего  . Таким образом, по показателям
. Таким образом, по показателям  и
и  предложенное распределение данных существенно отличается от нормального распределения.
предложенное распределение данных существенно отличается от нормального распределения.
6. Мода Мо= #Н/Д. Это означает, что множество исходных данных не содержит одинаковых данных.
4 Статистические методы изучения взаимосвязей явлений и процессов
4.1 Ковариация и корреляция
В исследованиях важной задачей является анализ зависимостей между рассматриваемыми переменными. Зависимость между переменными может быть функциональной и стохастической (вероятностной). Для оценки тесноты и направленности связи между изучаемыми переменными при их стохастической зависимости используются показатели: ковариация и корреляция.
Ковариация cov(x,y) случайных величин X и Y называют среднее произведение отклонений каждой пары значений X и Y в исследуемых массивах данных:
 . (4.1)
. (4.1)
Этот показатель используется в статистике редко и используется как промежуточный элемент расчета линейного коэффициента корреляции
 . (4.2)
. (4.2)
Для оценки степени тесноты линейной зависимости между явлениями используется линейный коэффициент корреляции
 . (4.3)
. (4.3)
Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или убывать) по линейному закону. Если случайные величины X и Y связаны точной линейной функциональной зависимостью y=ax+b, то  . Когда величины X и Y связаны произвольной вероятностной зависимостью, линейный коэффициент корреляции принимает значение в пределах
. Когда величины X и Y связаны произвольной вероятностной зависимостью, линейный коэффициент корреляции принимает значение в пределах  . В этом случае качественную оценку тесноты связи величин X и Y можно оценить с помощью шкалы Чеддока (таблица 4.1).
. В этом случае качественную оценку тесноты связи величин X и Y можно оценить с помощью шкалы Чеддока (таблица 4.1).
Таблица 4.1
| Теснота связи | Значение коэффициента корреляции при наличии: | |
| прямой связи | обратной связи | |
| Слабая | 0,1-0,3 | (-0,1)-(-0,3) |
| Умеренная | 0,3-0,5 | (-0,3)-(-0,5) |
| Заметная | 0,5-0,7 | (-0,5)-(-0,7) |
| Высокая | 0,7-0,9 | (-0,7)-(-0,9) |
| Весьма высокая | 0,9-0,99 | (-0,9)-(-0,99) |
Существуют различные модификации формул расчета линейного коэффициента корреляции
 ,
,
 . (4.4)
. (4.4)
Приведенные формулы справедливы для нахождения генерального коэффициента корреляции. Для расчета выборочного коэффициента корреляции необходимо заменить генеральные средние ( ) на выборочные средние (
) на выборочные средние ( ), а генеральные стандартные отклонения (
), а генеральные стандартные отклонения ( ) на выборочные стандартные отклонения (
) на выборочные стандартные отклонения ( ).
).
В Excel для выполнения расчетов используют функции КОВАР и КОРРЕЛ. Рассмотрим практику применения этих функций на примере.
Пример 4.1 В таблице 4.2 приведены показатели уровня образования, уровня преступности, отношение числа безработных к числу вакансий. Требуется установить наличие взаимосвязи между указанными показателями.
Таблица 4.2
| Область | Уровень образования | Отношение числа безработных к числу вакансий | Уровень преступности |
| Брянская | 735 | 22,3 | 908 |
| Владимирская | 788 | 10,8 | 791 |
| Ивановская | 779 | 52,9 | 804 |
| Калужская | 795 | 2,2 | 701 |
| Костромская | 740 | 10,4 | 685 |
| Москва | 902 | 0,4 | 496 |
| Московская обл. | 838 | 2,4 | 536 |
| Нижегородская | 763 | 5,4 | 936 |
| Орловская | 762 | 4,1 | 662 |
| Рязанская | 757 | 4,1 | 671 |
| Смоленская | 772 | 1 | 920 |
| Тверская | 764 | 4,2 | 1040 |
| Тульская | 764 | 2,1 | 809 |
| Ярославская | 755 | 25,1 | 882 |
Результат расчетов линейных коэффициентов корреляции представлены в виде таблицы 4.3.
Таблица 4.3
|
| Уровень образо- вания | Отноше- ние числа безработ- ных к числу вакансий | Уровень преступ- ности |
| Уровень образования | 1,00 |
|
|
| Отношение числа безработных к числу вакансий | -0,26 | 1,00 |
|
| Уровень преступности | -0,66 | 0,24 | 1,00 |
Таблица 4.3 симметрична, поэтому оставлены незаполненными три ячейки. Диагональные ячейки заполнять необязательно, т.к. они показывают взаимосвязь между одним и тем же параметром и поэтому имеем одинаковый результат равный 1,00.
После заполнения в Excel исходной таблицы 4.2 с параметрами данных, готовится таблица 4.3, куда заносится рассчитанные линейные коэффициенты корреляции. Так, что бы получить линейный коэффициент корреляции для параметров "уровень образования" и "уровень преступности" в Excel, делается активной ячейка в таблице 4.3 расчетов на пересечении этих параметров и вызывается функция КОРРЕЛ. В открывшемся окне функции КОРРЕЛ остается заполнить две ячейки: в первой указываются адреса данных параметра "уровень образования", а в другой - адреса данных параметра "уровень преступности". После щелчка по кнопке ОК получаем результат -0,66. Аналогично поступают с оставшимися двумя парами параметров.
Как показывают полученные результаты, между парами всех исследуемых показателей существует стохастические связи. Характер этих связей различен и состоит в следующем:
- связь "уровень образования" – "отношение числа безработных к числу вакансий" в соответствии с таблицей 4.1 является слабой и обратной ( =-0,26), т.е. с повышением уровня образования отношение числа безработных к числу вакансий уменьшается;
=-0,26), т.е. с повышением уровня образования отношение числа безработных к числу вакансий уменьшается;
- связь "уровень образования" – "уровень преступности" является заметной и обратной ( =‑0,66), т.е. с повышением уровня образования уровень преступности уменьшается;
=‑0,66), т.е. с повышением уровня образования уровень преступности уменьшается;
- связь "уровень преступности" - "отношение числа безработных к числу вакансий" является слабой и прямой ( =0,24), т.е. с увеличением отношения числа безработных к числу вакансий увеличивается и уровень преступности.
=0,24), т.е. с увеличением отношения числа безработных к числу вакансий увеличивается и уровень преступности.
При использовании приведенных оценок взаимосвязи процессов и явлений необходимо сделать следующие замечания. Во-первых, на практике коэффициент корреляции определяются чаще всего по выборочным данным, следовательно, полученные показатели отличаются от аналогичных показателей генеральной совокупности и выборочный коэффициент корреляции  представляет собой случайную величину. Во-вторых, наличие значимого линейного коэффициента корреляции
представляет собой случайную величину. Во-вторых, наличие значимого линейного коэффициента корреляции  не означает того, что существует причинно-следственная связь между факторами X и Y. Так
не означает того, что существует причинно-следственная связь между факторами X и Y. Так  =‑0,66 при оценке связи "уровень образования" – "уровень преступности" в примере 4.1 не означает, что существует причинно-следственная связь между уровнем образования и уровнем преступности (чем выше уровень образования, тем выше уровень преступность). Оба процесса могут развиваться независимо друг от друга, а корреляционная зависимость между ними носит ложный характер. В-третьих, невысокое значение линейного коэффициента корреляции не означает отсутствия взаимосвязи исследуемых факторов, т.к. эта связь может носить нелинейный характер. В-четвертых, перед вычислением линейного коэффициента корреляции необходимо построить корреляционное поле в координатах X-Y с целью выявления "выбросов" – координат точек, которые не отражают общую характеристику взаимосвязи исследуемых факторов.
=‑0,66 при оценке связи "уровень образования" – "уровень преступности" в примере 4.1 не означает, что существует причинно-следственная связь между уровнем образования и уровнем преступности (чем выше уровень образования, тем выше уровень преступность). Оба процесса могут развиваться независимо друг от друга, а корреляционная зависимость между ними носит ложный характер. В-третьих, невысокое значение линейного коэффициента корреляции не означает отсутствия взаимосвязи исследуемых факторов, т.к. эта связь может носить нелинейный характер. В-четвертых, перед вычислением линейного коэффициента корреляции необходимо построить корреляционное поле в координатах X-Y с целью выявления "выбросов" – координат точек, которые не отражают общую характеристику взаимосвязи исследуемых факторов.
В Excel для расчета ковариации и корреляции может быть использован режим
Сервис\Анализ данных…
В открывшемся окне выбирают инструмент анализа "Корреляция" или "Ковариация" и далее останется заполнить данными открывшееся окно. Так при выборе инструмента анализа "Корреляция" можно сразу получить таблицу 4.3.
Значимость полученных коэффициентов корреляции может быть проверена на основе t-критерия Стъюдента (при n<30). Для этого рассчитывается фактическое значение критерия, используя возможности Excel:
 ,
,
которое сопоставляется с табличным  , определяемым по числу степеней свободы
, определяемым по числу степеней свободы  и заданному уровню значимости (обычно
и заданному уровню значимости (обычно  ).
).
 может быть вычислено с помощью функции СТЬЮДРАСПОБР.
может быть вычислено с помощью функции СТЬЮДРАСПОБР.
Если  , коэффициент корреляции
, коэффициент корреляции  считается значительным, а связь X-Y реальной.
считается значительным, а связь X-Y реальной.
В примере n =14. Для  =‑0,66 получаем
=‑0,66 получаем  , а
, а  (получено через функцию =СТЬЮДРАСПОБР(0,05;12)). Откуда можно сделать вывод, что рассматриваемый коэффициент корреляции
(получено через функцию =СТЬЮДРАСПОБР(0,05;12)). Откуда можно сделать вывод, что рассматриваемый коэффициент корреляции  статистически значим и ошибка такого вывода не превышает 5%.
статистически значим и ошибка такого вывода не превышает 5%.
4.2 Линейная регрессия
Регрессионный анализ заключается в определении аналитического выражения связи зависимой случайной величины Y (называемой результативным признаком) с независимыми случайными величинами X1, X2, …, Xm (называемые факторами). Форма связи результативного признака Y с факторами X1, X2, …, Xm получила название уравнения регрессии. Различают линейную и нелинейную (квадратичная, экспоненциальная, логарифмическая и т.д.), парную и множественную (многофакторную) регрессии.
В Excel используется ряд статистических функций, связанных с регрессионным анализом.
Функция ЛИНЕЙН рассчитывает массив данных, описывающих уравнение линейной множественной (или парной) регрессии на основе метода наименьших квадратов. Синтаксис функции следующий
ЛИНЕЙН(известные_значения_ y; известные_значения_ x; конст; статистика)
Аргументы имеют следующее значение:
- известные_значения_ y – множество значений результативного признака Y;
- известные_значения_ x - множество значений факторных признаков Xi;
- конст – логическое значение, которое указывает требуется ли, чтобы свободный член a0 был равен 0;
- статистика - логическое значение, которое указывает требуется ли приводить дополнительную статистику по регрессии (если аргумент статистика=0, то дополнительная статистика по регрессии выведена не будет).
Функция ЛИНЕЙН находит коэффициенты  для уравнения прямой линии (регрессионного линейного уравнения). Это уравнение имеет вид
для уравнения прямой линии (регрессионного линейного уравнения). Это уравнение имеет вид
 ,
,
где  - теоретическое значение результативного признака, полученного путем подстановки соответствующих значений факторных признаков в уравнение регрессии.
- теоретическое значение результативного признака, полученного путем подстановки соответствующих значений факторных признаков в уравнение регрессии.
В случае оценки парной регрессии функция ЛИНЕЙН находит коэффициенты  для линейной регрессии
для линейной регрессии  . Порядок вычисления следующий:
. Порядок вычисления следующий:
- вводятся исходные данные или открывается существующий файл, содержащий анализируемые данные;
- выделяется область пустых ячеек (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1Í2 – для получения только оценок коэффициентов регрессии;
- активизируется инструмент «Мастер функций» и заполняются аргументы функции ЛИНЕЙН;
- в левой верхней ячейки выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, надо нажать на клавишу F2, а за тем ‑ на комбинацию клавиш Ctrl+Shift+Enter. Регрессионная статистика для парной регрессии выводится в порядке, приведенном в таблице 4.4.
Таблица 4.4
Значение коэффициента 
| Значение коэффициента 
|
Среднеквадратическое отклонение 
| Среднеквадратическое отклонение 
|
| Коэффициент детерминации R2 | Среднеквадратическое отклонение 
|
| F - статистика | Число степеней свободы |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |
Пример 4.2 Определить параметры уравнения линейной регрессии по данным о прибыли предприятий Y, величине оборотных средств X1 и стоимости основных фондов X2. Данные представлены в таблице 4.5.
Таблица 4.5
| Номер предпри- ятия | Прибыль Y, млн. руб | Величина оборот- ных средств X1, млн. руб | Стои- мость основных фондов X2, млн. руб |
| 1 | 188 | 129 | 510 |
| 2 | 78 | 64 | 190 |
| 3 | 93 | 69 | 240 |
| 4 | 152 | 87 | 470 |
| 5 | 55 | 47 | 110 |
| 6 | 161 | 102 | 420 |
В результате использования функции ЛИНЕЙН были найдены коэффициенты регрессии  , которые позволяют построить уравнение, выражающее зависимость прибыли предприятий Y от величины оборотных средств X1 и стоимости основных фондов X2:
, которые позволяют построить уравнение, выражающее зависимость прибыли предприятий Y от величины оборотных средств X1 и стоимости основных фондов X2:
 .
.
Функция ТЕНДЕНЦИЯ рассчитывает массив прогнозируемых значений результативного признака в соответствии с линейным трендом.
Воспользуемся примером 20 и определим какова возможна прибыль предприятия для величины оборотных средств X1 =95млн. руб и стоимости основных фондов X2 =380млн. руб. Синтаксис функции следующий
ТЕНДЕНЦИЯ(известные_значения_ y; известные_значения_ x; новые_значения_ x; конст)
В качестве новых значений x указываются значения, для которых функция ТЕНДЕНЦИЯ рассчитывает соответствующие значения  . В нашем примере новых значений x это 95 и 380, которые можно добавочно внести в исходную таблицу последней строчкой. А в конце столбца Y выполняется расчет с помощью функции ТЕНДЕНЦИЯ. Результат расчета приведен в таблице 4.6.
. В нашем примере новых значений x это 95 и 380, которые можно добавочно внести в исходную таблицу последней строчкой. А в конце столбца Y выполняется расчет с помощью функции ТЕНДЕНЦИЯ. Результат расчета приведен в таблице 4.6.
Таблица 4.6
| 5 | 55 | 47 | 110 |
| 6 | 161 | 102 | 420 |
| Прогнози- руемая прибыль | 141 | 95 | 380 |
Таким образом, прогнозируемая прибыль составит 141млн. руб.
Функция ТЕНДЕНЦИЯ может быть использована для прогнозов различного характера.
Пример 4.3 Известны данные об урожайности пшеницы, которые приведенные в таблице 4.7. Требуется определить, какова будет урожайность в последующие 3 года.
Таблица 4.7
|
| Год, x | Урожай- ность y, ц/га |
|
| 1995 | 25,0 |
|
| 1996 | 25,3 |
|
| 1997 | 25,7 |
|
| 1998 | 26,2 |
|
| 1999 | 26,9 |
|
| 2000 | 27,8 |
|
| 2001 | 28,7 |
|
| 2002 | 29,5 |
| Прогноз урожая | 2003 | 29,9 |
| 2004 | 30,7 | |
| 2005 | 31,5 |
В качестве новых значений x взяты 2003, 2004, 2005. Функция ТЕНДЕНЦИЯ сначала использована для нахождения урожайности в 2003 году, а затем эта функция распространена на остальные года прогноза.
С помощью функции ТЕНДЕНЦИЯ можно определить ошибку регрессии, что отражено в таблице 4.8.
Таблица 4.8
| Год, x | Урожай- ность y, ц/га | Урожай- ность по регрессии  , ц/га , ц/га
| Ошибка регрессии, 
|
| 1995 | 25,0 | 24,6 | 0,4 |
| 1996 | 25,3 | 25,2 | 0,1 |
| 1997 | 25,7 | 25,9 | -0,2 |
| 1998 | 26,2 | 26,6 | -0,4 |
| 1999 | 26,9 | 27,2 | -0,3 |
| 2000 | 27,8 | 27,9 | -0,1 |
| 2001 | 28,7 | 28,5 | 0,2 |
| 2002 | 29,5 | 29,2 | 0,3 |
Для этого в первой ячейке столбца "Урожайность по регрессии" заносится функция ТЕНДЕНЦИЯ, при этом первые два аргумента функции содержат абсолютные ссылки на данные столбцов "Год" и "Урожайность", а третий аргумент имеет ссылку на первый аргумент третьего столбца. После получения первого результата функция распространяется на остальные ячейки таблицы.
Функция ПРЕДСКАЗ рассчитывает для парной регрессии прогнозируемое значение результативного признака в соответствии с линейным трендом. Синтаксис функции
ПРЕДСКАЗ(x; известные_значения_ y; известные_значения_ x),
где x – точка данных, для которой предсказывается значение.
Эта функция является частным случаем функции ТЕНДЕНЦИЯ.
Пример 4.4 В таблице 4.9 приведены цены на однотипную квартиру за последние 6 месяцев. Требуется определить, какую цену можно ожидать в декабре.
Таблица 4.9
| Месяц | Стоимость квартиры, у.е. | Порядковый номер месяца |
| январь | 10500 | 1 |
| февраль | 10600 | 2 |
| март | 10750 | 3 |
| апрель | 10700 | 4 |
| май | 10780 | 5 |
| июнь | 10800 | 6 |
| Прогноз на декабрь | 11172 | 12 |
Функция ПРЕДСКАЗ помещена в последнюю ячейку второго столбца. А в качестве аргументов взяты x =12, известные_значения_ y – исходные данные из столбца "Стоимость квартиры"; известные_значения_ x - "Порядковый номер месяца" с цифрами от 1 до 6. В итоге получен ответ, что ожидаемая цена квартиры в декабре 11172 у.е. Но это при условии сохранения тенденции, которая наблюдалась за шесть рассматриваемых месяцев.
Функция СТОШYX рассчитывает для парной линейной регрессии стандартную ошибку оценки результативного признака Y. Синтаксис функции
СТОШYX(известные_значения_ y; известные_значения_ x).
Стандартная ошибка оценки результативного признака Y является мерой среднего рассеивания исходных точек вокруг подобранной линии регрессии. Таким образом, дается представление о надежности уравнения регрессии для проведения прогнозных расчетов. Для парной регрессии стандартная ошибка оценки определяется функцией СТОШYX по формуле
 , (4.5)
, (4.5)
где  - i -е фактическое значение результативного признака;
- i -е фактическое значение результативного признака;
 - i -е теоретическое значение результативного признака;
- i -е теоретическое значение результативного признака;
n – объем выборочной совокупности.
Рассчитаем стандартную ошибку  для примера 4.4. Искомое значение стандартной ошибки оценки стоимости квартиры
для примера 4.4. Искомое значение стандартной ошибки оценки стоимости квартиры  =53,64 у.е.
=53,64 у.е.
Для примера 4.3 стандартная ошибка  =0,31ц/га. Эта же ошибка рассчитана обычным путем дала тот же результат.
=0,31ц/га. Эта же ошибка рассчитана обычным путем дала тот же результат.
Замечание. Оценка стандартной ошибки во множественной регрессии осуществляется по формуле
 ,
,
где m – количество факторов x.
Во множественной регрессии для получения теоретических значений результативного признака  удобно использовать функцию ТЕНДЕНЦИЯ.
удобно использовать функцию ТЕНДЕНЦИЯ.
Приведенная формула используется и в функции ЛИНЕЙН при аргументе статистика=1.
4.3 Нелинейная регрессия
Все выше приведенные функции Excel используют линейную регрессию. Функция ЛГРФПРИБЛ описывает исходный массив данных уравнением экспоненциальной (показательной) регрессии, которая имеет следующий вид
 . (4.6)
. (4.6)
Аргументы функции ЛГРФПРИБЛ те же, что и для функции ЛИНЕЙН и работа с такой функцией аналогична работе с функцией ЛИНЕЙН.
Выравнивание по показательной кривой широко применяется в практике статистических исследований, поскольку характер динамики многих социально-экономических явлений соответствует гипотезе роста в геометрической прогрессии (увеличение объема промышленной продукции, рост капиталовложений, рост численности персонала в отрасли и т.д.).
Функция РОСТ рассчитывает массив прогнозируемых значений результативного признака в соответствии с экспоненциальной кривой. Работа с этой функцией аналогична работе с функцией ТЕНДЕНЦИЯ.
Пример 4.5 В таблице 4.10 прогноз прибыли предприятия, имеющего X1=135млн. руб и X2=530млн. руб выполнен с помощью функции РОСТ. Эта же функция применена для определения теоретической прибыли  . Стандартная ошибка оценки результативного признака
. Стандартная ошибка оценки результативного признака  определена по формуле для множественной регрессии (для n =6 и m =2).
определена по формуле для множественной регрессии (для n =6 и m =2).
Таблица 4.10
| Номер предпри- ятия | Прибыль Y, млн. руб | Величина оборот- ных средств X1 , млн. руб | Стои- мость основных фондов X2 , млн. руб | Прибыль теорети-ческая (экспоненц регрессия)
| Ошибка регрессии
| Стандартная ошибка оценки
|
| 1 | 352 | 115 | 510 | 319 | 32,72 | 23,28 |
| 2 | 72 | 59 | 190 | 72 | -0,45 | |
| 3 | 86 | 69 | 230 | 84 | 1,55 | |
| 4 | 310 | 87 | 470 | 332 | -22,16 | |
| 5 | 52 | 42 | 110 | 52 | 0,36 | |
| 6 | 161 | 135 | 445 | 169 | -7,80 | |
|
| Прогно- зируемая прибыль | Новое, X1 | Новое, X2 |
|
|
|
|
| 293,53 | 135 | 530 |
|
|
|
5 Статистические методы изучения динамики процессов
5.1 Скользящие средние и экспоненциальное сглаживание
Данные обычно делятся на два вида: перекрестные данные и временные ряды.
Перекрестные данные относятся к одному и тому же моменту времени, либо их временная принадлежность несущественна. Иное название таких данных – поперечный срез.
Временной ряд представляет собой последовательность изменений значений в наборе данных, которые наблюдаются через равные промежутки времени. Иное название таких данных – продольный срез.
Анализ временных рядов ставит две основные цели: определение природы временного ряда и прогноз будущих значений временного ряда. Для этого необходимо, чтобы модель ряда была идентифицирована и формально описана.
Анализ временных рядов предполагает, что данные содержат систематическую составляющую и случайную ошибку (шум), которая затрудняет обнаружение регулярных компонент. Одна из моделей временного ряда, содержит его разложение на систематическую d и случайную e составляющие
 . (5.1)
. (5.1)
В свою очередь, в систематической компоненте d выделяется две составляющие:
- тренд tr;
- циклическая компонента c.
В итоге, модель временного ряда принимает вид
 . (5.2)
. (5.2)
Для выделения тренда и циклической компоненты, а, следовательно, сведения временного ряда к стационарности, используются:
- метод скользящей средней;
- метод экспоненциального сглаживания.
Метод скользящей средней. Это один из старых и широко известных способов сглаживания временного ряда. Сглаживание – способ локального усреднения данных, при котором несистематические компоненты взаимно погашают друг друга. В результате сглаживания новый полученный ряд скользящих средних дает представление об общей тенденции поведения ряда.
Метод скользящей средней состоит в том, что исходный эмпирический временной ряд  преобразуется в ряд сглаженных значений по формуле
преобразуется в ряд сглаженных значений по формуле
 , (5.3)
, (5.3)
где p – размер окна (интервал времени, выбранный заранее);
j – порядковый номер уровня в окне сглаживания;
m – величина, определяемая по формуле m =(p -1)/2.
Метод скользящей средней приемлем для временного ряда, если его графическое изображение напоминает прямую линию. Если временной ряд имеет явно нелинейный характер, то целесообразно использовать метод экспоненциального сглаживания.
Метод экспоненциального сглаживания. Этот метод, как и предыдущий, представляет собой способ усреднения значений эмпирического временного ряда
 .
.
Однако, в отличие от метода скользящей средней, в определении экспоненциальной средней участвуют все наблюдения исходного временного ряда, но с разными весовыми коэффициентами. Формула метода простого экспоненциального сглаживания имеет следующий вид
 , (5.4)
, (5.4)
где 0<α<1 – коэффициент экспоненциального сглаживания.
Результат сглаживания зависит от параметра α. Чем больше α, тем сильнее сказывается фактические значения, чем меньше α, тем сильнее сказываются теоретические сглаженные значения. При α=0 полностью игнорируются фактические значения, а при α=1 – теоретические сглаженные значения предыдущего периода.
В Excel реализовано два режима работы "Скользящее среднее" и "Экспоненциальное сглаживание". На рис.5.1 показано окно "Скользящее среднее", которое появится после выбора
Сервис\Анализ данных…
и в открывшемся диалоговом окне выделения инструмента анализа "Скользящее среднее".

Рис.5.1
Поле "Входной интервал" – вводится ссылка на ячейки, которые содержат анализируемые данные.
Флажок "Метки…" устанавливается в активное состояние, если первая строка (столбец) во входном диапазоне содержит заголовки.
"Интервал" – вводится размер окна сглаживания p (по умолчанию p =3).
"Выходной интервал" - в поле необходимо ввести ссылку на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона определяется автоматически.
В положении "Новый рабочий лист" открывается новый рабочий лист, куда, начиная с ячейки А1 вставляются результаты анализа.
В положении "Новая рабочая книга" открывается новая рабочая книга, куда на первый лист, начиная с ячейки А1, вставляются результаты анализа.
"Вывод графика" – устанавливается в активное состояние для автоматической генерации на рабочем листе графиков фактических и теоретических значений временного ряда.
"Стандартные погрешности" - устанавливается в активное состояние, если требуется включить в выходной диапазон столбец, содержащий стандартные погрешности.
На рис.5.2 приведено диалоговое окно режима "Экспоненциальное сглаживание". От предыдущего окна "Экспоненциальное сглаживание" отличается параметром "Фактор затухания", куда вводится значение коэффициента экспоненциального сглаживания α. По умолчанию α=0,3.

Рис.5.2
Пример 5.1 В таблице 5.1 приведены в трех первых столбцах данные о средней реализации продуктов сельскохозяйственного производства магазинами потребительской кооперации города за 1997-2000 годы. Требуется выявить за указанный период времени основную тенденцию развития данного экономического процесса и характер его сезонных колебаний.
Таблица 5.1
| Год | Квартал | Размер реализа- ции y, тыс. руб | Сглажен- ные уровни | Стандарт- ные погреш- ности |
| 1997 | 1 | 175 | #Н/Д | #Н/Д |
| 2 | 263 | #Н/Д | #Н/Д | |
| 3 | 326 | #Н/Д | #Н/Д | |
| 4 | 297 | 265,25 | #Н/Д | |
| 1998 | 1 | 247 | 283,25 | #Н/Д |
| 2 | 298 | 292,00 | #Н/Д | |
| 3 | 366 | 302,00 | 40,17 | |
| 4 | 341 | 313,00 | 39,47 | |
| 1999 | 1 | 420 | 356,25 | 47,38 |
| 2 | 441 | 392,00 | 53,26 | |
| 3 | 453 | 413,75 | 46,88 | |
| 4 | 399 | 428,25 | 47,07 | |
| 2000 | 1 | 426 | 429,75 | 34,68 |
| 2 | 449 | 431,75 | 26,02 | |
| 3 | 482 | 439,00 | 27,46 | |
| 4 | 460 | 454,25 | 23,42 |
В последних двух столбцах таблицы 5.1 приведены результаты применения режима "Скользящее среднее", где указывались:
- "Входной интервал" – столбец y;
- "Интервал" – 4 (р =4);
- "Вывод графика" и "Стандартные погрешности" – активированы.
После получения значения были округлены до второго десятичного знака. А полученный график представлен на рис.5.3.

Рис.5.3
Однако, если размер окна сглаживания р является четным числом, рассчитанное усредненное значение  нельзя сопоставить какому-либо определенному моменту времени t. В этом случае необходимо применить так называемую процедуру центрирования.
нельзя сопоставить какому-либо определенному моменту времени t. В этом случае необходимо применить так называемую процедуру центрирования.
В примере р =4, т.е. рассматривалось сразу четыре момента времени и средний момент времени t может быть отнесен только к середине между двумя кварталами, находящимися в середине окна сглаживания.
Процедура центрирования заключается в следующих действиях.
Первый сглаженный уровень (265,25) записывается между 2 и 3 кварталами 1997 года, второй (283,25) – между 3 и 4 кварталами 1997 года и т.д. Далее применяется процедура центрирования. Для 3 квартала 1997 г. определяется срединное значение между первым и вторым сглаженными уровнями: (265,25+283,25)/2=174,25; для 4 квартала 1997 г центрируются второй и третий сглаженные уровни: (283,25+292,00)/2=287,6 т.д. Результат центрирования приведен в таблице 5.2 и на рис.5.4.
Таблица 5.2
| Год | Квартал | Размер реализа- ции y, тыс. руб | Сглажен- ные уровни, | Стандарт- ные погреш- ности | Сглажен- ные уровни с центриро- ванием |
| 1997 | 1 | 175 | #Н/Д | #Н/Д |
|
| 2 | 263 | #Н/Д | #Н/Д |
| |
| 3 | 326 | #Н/Д | #Н/Д | 274,25 | |
| 4 | 297 | 265,25 | #Н/Д | 287,63 | |
| 1998 | 1 | 247 | 283,25 | #Н/Д | 297,00 |
| 2 | 298 | 292,00 | #Н/Д | 307,50 | |
| 3 | 366 | 302,00 | 40,17 | 334,63 | |
| 4 | 341 | 313,00 | 39,47 | 374,13 | |
| 1999 | 1 | 420 | 356,25 | 47,38 | 402,88 |
| 2 | 441 | 392,00 | 53,26 | 421,00 | |
| 3 | 453 | 413,75 | 46,88 | 429,00 | |
| 4 | 399 | 428,25 | 47,07 | 430,75 | |
| 2000 | 1 | 426 | 429,75 | 34,68 | 435,38 |
| 2 | 449 | 431,75 | 26,02 | 446,63 | |
| 3 | 482 | 439,00 | 27,46 |
| |
| 4 | 460 | 454,25 | 23,42 |
|

Рис.5.4
Рассчитанные сглаженные уровни не только дают представление об общей тенденции поведения изучаемого временного ряда, но могут быть использованы для вычисления индексов сезонности  , совокупность которых характеризует сезонную волну исследуемого процесса. Средние индексы сезонности определяются по формуле
, совокупность которых характеризует сезонную волну исследуемого процесса. Средние индексы сезонности определяются по формуле
 , (5.5)
, (5.5)
где  - исходные уровни ряда;
- исходные уровни ряда;
 - сглаженные уровни ряда;
- сглаженные уровни ряда;
u – число одноименных периодов.
В таблице 5.3 рассчитаны для каждого квартала отношение  и получены средние индексы сезонности для каждого квартала. Так для 1 квартала средний индекс сезонности определен так: (0,832+1,043+0,978)/3=0,951 (или 95,1%). Исчисленные показатели
и получены средние индексы сезонности для каждого квартала. Так для 1 квартала средний индекс сезонности определен так: (0,832+1,043+0,978)/3=0,951 (или 95,1%). Исчисленные показатели  являются средними индексами сезонных колебаний продажи сельскохозяйственной продукции по кварталам. Сезонная волна товарооборота сельскохозяйственной продукции (прирост в процентах к среднему уровню) приведена на рис.5.5.
являются средними индексами сезонных колебаний продажи сельскохозяйственной продукции по кварталам. Сезонная волна товарооборота сельскохозяйственной продукции (прирост в процентах к среднему уровню) приведена на рис.5.5.
Таблица 5.3
| Квартал | Размер реализа- ции y, тыс. руб | Сглажен- ные уровни с центриро- ванием |
|
| 1 | 175 |
|
|
| 2 | 263 |
|
|
| 3 | 326 | 274,25 | 1,189 |
| 4 | 297 | 287,63 | 1,033 |
| 1 | 247 | 297,00 | 0,832 |
| 2 | 298 | 307,50 | 0,969 |
| 3 | 366 | 334,63 | 1,094 |
| 4 | 341 | 374,13 | 0,911 |
| 1 | 420 | 402,88 | 1,043 |
| 2 | 441 | 421,00 | 1,048 |
| 3 | 453 | 429,00 | 1,056 |
| 4 | 399 | 430,75 | 0,926 |
|
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
 Сейчас читают про:
|
 2018-03-08
2018-03-08 214
214







