Эвристический поиск в пространстве состояний

Представление пространства состояний. Пространство состояний может быть представлено как граф G (X, E), где  - множество (в общем случае бесконечное) вершин графа, каждая из которых отождествляется с одним из состояний ;

 - множество дуг или ребер графа бесконечное, если бесконечно множество X. Все ребра в графе являются взвешенными, т.е. им присвоено некоторое значение (вес), позволяющее оценить с помощью оценочной функции  переход от одного состояния к другому;

Г (x) – преобразование, порождающее все дочерние вершины
от   x.

| Г (x) | - количество дочерних вершин от x, т.е. вершин, соединенных с x дугой.

Структура графа пространства состояний представляется в виде матрицы весов (значений оценочной функции) графа: , , в которой  соответствует значение веса ребра () или 0, если вершины ,  не связаны ребром ().

Если граф пространства состояний не является простым, то он должен быть преобразован в него посредством исключения всех петель и заменой каждого множества параллельных ребер кратчайшим ребром (ребром с наименьшим весом) из этого множества, каждое неориентированное ребро заменяется парой ориентированных.

В множестве вершин X выделяют подмножество вершин , соответствующее множеству начальных состояний  и , соответствующих множеству конечных состояний .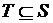

Определим путь в графе G как , где  и .

Если , , то решение задачи эвристического поиска в пространстве состояний сводится к задаче поиска пути r на графе G. Сумма всех ребер в пути называется длиной пути.

Алгоритмы поиска различаются порядком раскрытия вершин: поиск в ширину и поиск в глубину, а также отличаются полнотой просмотра пространства состояний.

Эвристический алгоритм поиска в графе пространства состояний. Пространство состояний можно исследовать как с помощью слепого перебора, так и с применением эвристического (упорядоченного) поиска. Идея, лежащая в основе большинства эвристических алгоритмов, состоит в том, чтобы оценивать перспективность нераскрытых вершин пространства состояний, и выбирать для продолжения поиска наиболее перспективную вершину.

Для этого используется эвристическая оценочная функция. Эта функция определяется на множестве вершин пространства состояний и принимает числовые значения, которые могут интерпретироваться как перспектива раскрытия вершины или вероятность ее расположения на решающем пути.

 

Далее приводятся основные шаги алгоритма эвристического
поиска.

Пусть имеются: одна начальная вершина ;

S – множество уже выбранных вершин,  - множество вершин – кандидатов в S, при этом ;

 - множество конечных вершин;

x – текущая вершина;

 - дочерняя вершина x.

Тогда алгоритм поиска в графе пространства состояний заключается в поиске пути, начиная из вершины , просматривая граф в ширину, и представляется следующими шагами.

1. Поместить  в  и вычислить оценочную функцию .

2. Выбрать такую , что  и поместить ее в S, изъяв из . В случае равенства выбрать любую.

3. Если  - путь найден, иначе продолжить.

4. Найти все , если , то перейти к шагу 2, иначе вычислить все .

5. Для каждого :

а) если , то поместить  в ;

б) если , то сопоставить  наименьшее из старой и вновь полученной оценки ;

в) если , то сопоставить  наименьшее из старой и вновь полученной оценки , поместить  в  (изъяв ее из S);

г) в остальных случаях не изменять S и .

6. Перейти к шагу 2.

Пункты 5(б), 5(в) отражают действие алгоритма в случае, когда оператор Г порождает уже рассмотренные вершины, которые к этому моменту находятся в S или , поэтому этим вершинам приписываются наименьшие из возможных оценочных функций.

В качестве примера рассмотрим игру в восемь. В ней используется восемь (начиная с первой) подвижных фишек, расположенных в клетках квадрата 3x3. Одна клетка этого квадрата остается всегда пустой. Передвигая соседние с ней фишки, необходимо добиться упорядоченного расположения их номеров.

На рис.1 показано дерево игры, построенного алгоритмом эвристического перебора с указанной оценочной функцией. Оценка каждой вершины приведена рядом с ней внутри кружка. Отдельно стоящие цифры показывают порядок, в котором раскрывались вершины.

Рис.1. Пример дерева поиска

Рассмотрим процесс построения дерева поиска пути на основе изложенного ранее алгоритма. Результаты поиска будем представлять в виде двух множеств S и , содержащих вершины с указанием в скобках значений весов входящих в них дуг. В качестве оценочной функции будем использовать следующую: ,

где D(x) – глубина вершины x или число ребер дерева на пути от этой вершины к начальной;

K(x) – число фишек позиции – вершины x, лежащие не на «своем» месте.

1.

Вершины , ,  являются дочерними для вершины . Вершина  имеет наименьшее значение оценочной функции, поэтому она исключается из  и добавляется в S.

2.

Новые вершины в  есть дочерние для последней добавленной вершины. Вершины ,  имеют одинаковую минимальную оценку, выберем из них любую и добавим в S.

3.

4.

5.

6.

Последняя вершина, добавленная в S , следовательно, путь найден: .

В ходе решения задачи может возникнуть ситуация, когда при выборе вершин для множества S совпадают их оценочные функции, в этом случае необходимо проанализировать все возможные альтернативные пути, начиная с данного этапа.

Алгоритм поиска пути на графе. В ряде случаев при наличии графа, описывающего полное пространство состояний и динамически изменяющейся игровой ситуации, возникает задача поиска за минимальное время короткого пути, ведущего из начальной ситуации  в одно из конечных . Для ее решения существует несколько алгоритмов, один из которых состоит в следующем.

Рассматриваемый алгоритм определяет расстояние между вершинами в простом орграфе с неотрицательными весами. Алгоритм, начиная из вершины , просматривает граф в ширину, помечая вершины  значениями – метками их расстояний от . Временная метка вершины  - это минимальное расстояние от  до , когда в определении пути на графе учитываются не все маршруты из  в . Окончательная метка  содержит минимальное расстояние на графе от  до . Таким образом, в каждый момент времени работы алгоритма некоторые вершины будут иметь окончательные метки, а остальная их часть – временные. Алгоритм заканчивается, когда вершина  получает окончательную метку, то есть расстояние
от  до .

Вначале вершине  присваивается окончательная метка 0 (нулевое расстояние до самой себя), а каждой из остальных  - 1 вершин присваивается временная метка  (бесконечность). На каждом шаге алгоритма одной вершине с временной меткой присваивается окончательная и поиск продолжается дальше. На каждом шаге вершины меняются следующим образом.

1. Если имеется дуга из  в , то каждой вершине , не имеющей окончательной метки, присваивается новая временная метка – наименьшая из ее временной и числа ( +окончательная метка ), где  - вершина, которой присвоена окончательная метка на предыдущем шаге.

2. Определяется наименьшая из всех временных меток, которая становится окончательной меткой своей вершины, в случае равенства меток выбирается любая из них.

Циклический процесс п.1, п.2 продолжается до тех пор, пока вершина  не получит окончательной метки, которая представляет собой короткое расстояние от этой вершины до начала .

Рассмотрим работу изложенного выше алгоритма для графа, заданного в виде матрицы весов графа (табл.1).

Таблица1

Матрица весов графа

W	X0	X1	X2	X3	X4	X5	X6
X0	0	7	2	0	0	0	0
X1	0	0	0	1	5	0	10
X2	0	3	0	5	0	0	0
X3	0	0	0	0	3	7	0
X4	0	0	8	0	0	5	2
X5	0	0	0	0	5	0	6
X6	0	0	0	0	0	0	0

Граф со структурой, соответствующей данной матрице, представлен на рис.2.

Рис.2. Граф для демонстрации работы алгоритма

Процесс назначения меток вершинам графа на каждом шаге представлен в табл. 2.

Таблица 2