Закон распределения дискретной случайной величины. Полигон распределения дискретной с.в

Дискретная случайная величина Х распределена по биномиальному закону, если она принимает значения 0,1,2…, m …, n … с вероятностями, которые находятся по формуле Бернулли:

Xi	0	1	…	m	…	n
Pi	Q в степ n	n*p*q в степ n-1	…		…	p в степ n

Pn (x=0)=Cn d степ 0 * р в степ 0 * q в степ n = q в степ n

Pn (x=1)=Cn d степ 1 * р в степ 1 * q в степ n-1 = n*p*q в степ n-1

Pn (x=n)=Cn d степ n * р в степ n * q в степ n-n = 1*p в степ n *1= р в степ n

Математическое ожидание, дисперсия и среднее квадратическое отклонение дискретной с.в.

Математическим ожиданиемдискретной случайной величины называ-ется сумма произведений ее возможных значений на соответствующие им вероятности:

М (Х) = х ₁ р ₁ + х ₂ р ₂ + … + х_пр_п.

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Дисперсия, как характеристика разброса случайной величины, имеет один недостаток. Если, например, Х – ошибка измерения имеет размерность ММ, то дисперсия имеет размерность 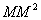. Поэтому часто предпочитают пользоваться другой характеристикой разброса – средним квадратическим отклонением, которое равно корню квадратному из дисперсии.