Метод вариации произвольных постоянных для нахождения частного решения неоднородного дифференциального линейного уравнения 2-го порядка

Пусть

,                                             (*)

причем  – общее решение соответствующего однородного дифференциального уравнения. Для нахождения общего решения (*) необходимо найти . Согласно методу Лагранжа,  ищется в виде:

    ,

где  и  – неизвестны. Так как неизвестных функций две, а уравнение одно, то накладывается еще одно произвольное условие с целью упростить решение. Пусть

и потребуем, чтобы

    ,

– это и есть дополнительное условие, то есть .

    Далее,

    .

Подставим последнее выражение в уравнение (*), получим

    ,

поскольку  и . Получили следующую систему уравнений:

    .

Эта система имеет решение относительно  и , так как  (  и  линейно независимы). Отсюда

    ,                   ,

    ,               ,

    ,

    .

На практике можно пользоваться сразу готовыми формулами или выводить их для конкретного уравнения.

Пример:

    Рассмотрим дифференциальное уравнение

.

Общее решение соответствующего однородного дифференциального уравнения есть

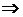
        и .

Имеем систему уравнений

    ,

    .

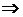
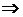
Заключение:

    Таким образом, линейное дифференциальное уравнение 2-го порядка можно решить, если суметь найти частное решение неоднородного уравнения и общее решение соответствующего однородного уравнения. Стандартного процесса нахождения общего решения неоднородного уравнения нет. Многие дифференциальные уравнения не интегрируются в элементарных функциях.

Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и приводящиеся к ним