Пусть  и
и  – решения (2), следовательно,
– решения (2), следовательно,
 . (3)
. (3)
Умножим первое из этих уравнений на  , а второе – на
, а второе – на  и сложим их, получим
и сложим их, получим
 , (
, ( )
)
что равносильно
 . (
. ( )
)
Это означает, что  двух решений уравнения (2) есть одно из решений дифференциального уравнения (1). Рассмотрим уравнение
двух решений уравнения (2) есть одно из решений дифференциального уравнения (1). Рассмотрим уравнение
 . (
. ( )
)
Решая его, получим:

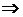

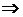
 .
.
Поскольку начальное условие  произвольно, то и
произвольно, то и  является фактически произвольной константой:
является фактически произвольной константой:  .
.
Так как определитель Вронского есть одно из решений ( ), то для него также справедлива следующая формула:
), то для него также справедлива следующая формула:
 . (4)
. (4)
Формула Остроградского-Лиувилля справедлива для любых двух решений уравнения (2).
Функция 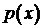 непрерывна, следовательно,
непрерывна, следовательно,  и справедливо следующее утверждение: вронскиниан
и справедливо следующее утверждение: вронскиниан  либо тождественно равен нулю, если
либо тождественно равен нулю, если  , либо не равен нулю ни при одном
, либо не равен нулю ни при одном  , если
, если  . Таким образом, определитель Вронского для фундаментальной системы решений не только тождественно не равен нулю, но и не обращается в ноль ни при одном
. Таким образом, определитель Вронского для фундаментальной системы решений не только тождественно не равен нулю, но и не обращается в ноль ни при одном  . Существенной является непрерывность
. Существенной является непрерывность 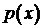 .
.
|
|
|
 2018-02-14
2018-02-14 504
504








