Теорема:
Любое однородное линейное дифференциальное уравнение имеет фундаментальную систему решений.
Доказательство:
Рассмотрим дифференциальное уравнение

и две системы начальных условий:
 ,
,  ,
,  ,
,
 ,
,  ,
,
где
 .
.
Пусть  и
и  – частные решения соответствующих задач Коши. Докажем, что они образуют фундаментальную систему:
– частные решения соответствующих задач Коши. Докажем, что они образуют фундаментальную систему:
 .
.
Теорема доказана.
Основная теорема:
Общее решение линейного однородного дифференциального уравнения 2-го порядка является линейной комбинацией с произвольными постоянными коэффициентами любых двух решений этого уравнения, образующих фундаментальную систему решений. Другими словами, общее решение линейного однородного дифференциального уравнения 2-го порядка есть сумма двух частных решений линейно независимых решений, умноженных на произвольные постоянные.
Доказательство:
Пусть  и
и  – фундаментальная система решений. Составим линейную комбинацию
– фундаментальная система решений. Составим линейную комбинацию
 ,
,
где  ,
,  есть произвольные постоянные. Надо доказать, что любое частное решение можно получить из
есть произвольные постоянные. Надо доказать, что любое частное решение можно получить из  выбором
выбором  и
и  .
.
|
|
|
Пусть  есть решение задачи Коши для начальных условий
есть решение задачи Коши для начальных условий
 ,
,  ,
,  .
.
Положим  , тогда
, тогда
 ,
,
 ,
,
отсюда
 и
и  .
.
Так как  , то
, то  и есть общее решение.
и есть общее решение.
Применение формулы Остроградского-Лиувилля
Зная одно частное решение (2), не равное нулю, можно с применением формулы Остроградского-Лиувилля найти фундаментальную систему и, следовательно, общее решение (2), вычислив два неопределённых интеграла.
Пусть  есть известное решение и нужно найти
есть известное решение и нужно найти  . Так как
. Так как  и
и  , то при
, то при  получаем:
получаем:

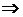
 .
.
И, наконец, при 
 .
.
Пример. Рассмотрим дифференциальное уравнение
 ,
,  .
.
Тогда
 .
.
Общее решение будет:
 .
.
Линейные неоднородные дифференциальные уравнения 2-го порядка
 2018-02-14
2018-02-14 266
266








