Уравнение плоской волны

Уравнением волны называется выражение, которое определяет смещение колеблющейся частицы как функцию координат и времени:

Пусть плоская волна распространяется вдоль оси x, а точка O является источником колебаний и колеблется по закону:

(48)

t – время, отсчитанное от начала колебаний т. O.

Выберем на прямой, вдоль которой распространяется волна, произвольную точку M на расстоянии x от источника колебаний. Колебания дойдут до точки M через промежуток времени , где v – скорость распространения волны.

Точка M начнет колебаться позже т. O, но с той же амплитудой A и частотой w. Тогда смещение точки M из положения равновесия запишется в виде:

(49)

Для любой точки:

(50)

Это уравнение позволяет определить смещение из положения равновесия любой точки волны и называется уравнением плоской волны, распространяющейся вдоль оси x.

Аргумент тригонометрической функции называется фазой волны:

(51)

Преобразуем это выражение, для чего введем понятие длины волны.

Изобразим моментальный снимок волны, т.е. график зависимости

для фиксированного момента времени t.

Расстояние между ближайшими точками, колеблющимися в одинаковой фазе, называется длиной волны. Длину волны можно определить так же, как расстояние, пройденное волной за период колебаний частиц среды:

(52)

Преобразуем (51) с учетом (52)

(53)

Тогда уравнение волны, распространяющейся вдоль оси x, запишется в виде:

(54)

Введем величину:

(55)

которая называется волновым числом, и придем к следующему уравнению плоской волны, распространяющейся вдоль оси x:

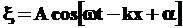(56)

Разность фаз:

Фазовая скорость.

Рассмотрим некоторую волновую поверхность, например, плоскость, содержащую т. M. Очевидно, фаза волны в этой плоскости будет меняться с течением времени. Чтобы фаза оставалась постоянной, плоскость должна перемещаться с некоторой скоростью вдоль оси x.

Скорость перемещения определенной фазы волны называется фазовой скоростью .

Найдем фазовую скорость из условия, что

и :

откуда: (57)

Фазовая скорость равна скорости распространения волны.

Волновое уравнение.

Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы получить волновое уравнение, воспользуемся для простоты уравнением плоской волны, распространяющейся вдоль оси x:

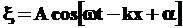
и найдем и :

(58)

(59)

Из сравнения (58) и (59) получим волновое уравнение:

(60)

Если волна распространяется в произвольном направлении, то волновое уравнение примет вид:

(61)

Групповая скорость.

Совокупность волн, мало отличающихся друг от друга по частоте, называется волновым пакетом или группой волн. Точка, в которой амплитуда колебаний группы волн максимальна, называется центром группы волн. Скорость, с которой распространяется максимум колебательного процесса (скорость центра группы волн), называется групповой скоростью. Групповая скорость – скорость передачи энергии группой волн.

В зависимости от частоты колебаний может меняться и скорость распространения волны. Зависимость скорости распространения волны от частоты колебаний частиц среды называется дисперсией.

Волновое число k равно:

Дисперсия приводит к нарушению линейной зависимости между k и w. Зависимость w=w(k) называется дисперсионным уравнением или законом дисперсии.

Если среда не обладает дисперсией, то все гармонические волны независимо от частоты распространяются с одной и той же фазовой скоростью и пакет ведет себя как стационарная волна, т.е. , если в среде имеет место дисперсия, то .

Найдем связь между групповой и фазовой скоростями. Преобразуем выражение для фазы волны (51):

(62)

Для сохранения пакета волн необходимо, чтобы в центре пакета находился набор когерентных волн, распространяющихся с одинаковыми скоростями. Для таких волн изменение фазы в зависимости от длины волны должно быть равно нулю:

(63)