Нахождение коэффициентов многофакторной линейной модели прогнозирования

Линейная модель множественной регрессии. У=а₀+а₁х₁+ а₂х₂+…+ а_mх_m+e

Параметры определяются с помощью методов наименьших квадратов.

 Для этого проведем все рассуждения в матричной форме. Введем следующие матричные обозначения:

;

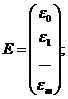
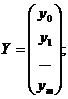
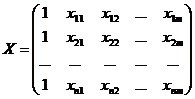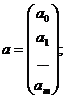
где У вектор n значений результативного показателя.

Х – матрица n значений m независимых переменных; а матрица параметров

У=Х∙а+ε.

Заметим, что а – выборочные оценки совокупности.

Итак, метод наименьших квадратов требует мин-ии суммы квадратов отклонений исходных модели значений

,

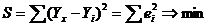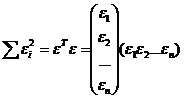
Далее: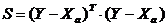

Из матричной алгебры известно, что 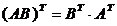, тогда:

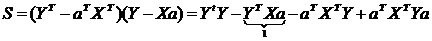
1 – это есть матрица размерностью 1Х1, т.е. число-скаляр, а скаляр при трансформировании не меняется, поэтому 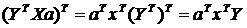Þ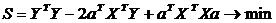

Согласно условию экстремума S по а =0

;

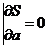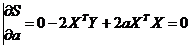
2Х^ТY+2aX^TX=0

X^TY=aX^TX

Для погашения а умножим обе части этого уравнения на (ХТХ)-1, тогда

а= (X^TХ)^-1∙X^TY

Решение задачи нахождения матицы, а возможно лишь в том случае, если строки и столбцы матрицы Х линейно независимы.

 

 

Система нормальных уравнений для многофакторных моделей прогнозирования.

Параметры уравнения множественной регрессии оценивают­ся, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки пара­метров регрессии.

 

Так, для уравнения

 

система нормальных уравнений составит

 

Ее решение может быть осуществлено методом определителей:

где Δ– определитель системы; Δа,Δb1,…,Δbp– частные определители.

 

Линейное уравнение множественной регрессии, вычисление статистических характеристик.