2018-02-12
223
РАБОТЕ № 8
Пример 1. Два стрелка производят по одному выстрелу по одной мишени. Первый попадает в мишень с вероятностью 0,8, второй - с вероятностью 0,6. Найдите вероятность того, что: а) оба стрелка попадут в мишень, б) оба стрелка промахнутся, в) только один стрелок попадет, г) хотя бы один стрелок попадет в мишень.
Решение. Пусть событие А означает, что первый стрелок попал в мишень, событие В - попал второй. По условию Р (А) = 0,8, Р (В) = 0,6.
а) Пусть событие С - оба стрелка попали в мишень, тогда С = АВ. Поэтому, учитывая независимость событий А и В, по теореме умножения вероятностей имеем
Р (С) = Р (АВ) = Р (А) Р (В) = 0,8 × 0,6 = 0,48.
б) Перейдем к противоположным событиям, которые состоят в том, что первый стрелок промахнулся 
, второй стрелок промахнулся 
. Тогда событие D = означает, что оба стрелка промахнулись.
Р (D) = Р ( ) = Р () P ()= (1 – Р (А)) (1 – Р (В)) = =0,2 × 0,4 = 0,08.
в) Событие Е –только один стрелок попал – можно представить в виде Е = А + В . События А и В несовместные. Поэтому, применяя теорему сложения вероятностей несовместных событий, получим
|
|
|
Р (Е) = Р (А + В ) = P (А )+ Р (В ) =
= P (А) Р ()+ Р (В) Р () = 0,8 × 0,4 + 0,6 × 0,2 = 0,44.
г) Вероятность появления хотя бы одного из совместных событий А, В равна разности между единицей и вероятностью произведения противоположных событий , . Пусть событие F – хотя бы один стрелок попал. Тогда
Р (F) = 1 – Р ( ) = 1 – Р () P () = 1 – 0,2 × 0,4 = 0,92.
Пример 2. В первой урне 2 белых и 3 черных шара, во второй – 7 белых и 1 черный. Из первой урны в первую переложили 2 шара, затем наудачу извлекли шар из второй урны. Найдите вероятность того, что выбранный из второй урны шар – белый.
Решение. Если событие А может произойти только совместно с одним из событий Н 1 , Н 2,..., Н 
, образующих полную группу несовместных событий (гипотез), то вероятность Р (А) появления события определяется по формуле полной вероятности: Р (А) = 
Р (H 
) Р (А/H ), где Р (H ) - вероятность гипотезы H , Р (А/H ) - условная вероятность события А при этой гипотезе.
Вероятность извлечения белого шара из второй урны после добавления двух шаров из первой урны зависит от состава шаров (по цвету) в этой урне. При этом возможны следующие гипотезы:
Н 1 – из первой урны во вторую переложены два белых шара,
Н 2 – из первой урны во вторую переложен один белый и один черный шар,
Н 3 – из первой урны во вторую переложены два черных шара.
Найдем вероятности этих гипотез. Вероятность каждой гипотезы связана с вероятностью извлечения соответствующих шаров из первой урны. Тогда получим
Р (Н 1 ) = 
= 0,1,
Р (Н 2) = 
= 0,6,
Р (Н 3) = 
= 0,3.
|
|
|
Пусть А – событие, состоящее в извлечении белого шара из второй урны, если предварительно имела место одна из гипотез Нi. Условные вероятности события А будут:
Р (А/H 1) = 9/10, Р (A/Н 2) = 8/10, Р (A/Н 3) = 7/10.
По формуле полной вероятности найдем вероятность извлечения белого шара из второй урны
Р (А) = Р (H 1) Р (А/H 1) + Р (H 2) Р (А/H 2) + Р (H 3) Р (А/H 3) =
= 0,1× 0,9 + 0,6× 0,8 + 0,3× 0,7 = 0,78.
Пример 3. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго – 0,5, для третьего – 0,8. Мишень не поражена. Найдите вероятность, что выстрелы произведены первым стрелком.
Решение. Если вероятности гипотез до опыта были Р (Н 1), Р (Н 2),..., Р (Н 
), а в результате опыта появилось событие А, то условная вероятность Р (Н / A) с учетом появления события А вычисляется по формуле Бейеса:
Р (Н / A) = 
.
Возможны три гипотезы: H 1–на линию огня вызван первый стрелок; H 2 –на линию огня вызван второй стрелок; H 3 –на линию огня вызван третий стрелок. Так как вызов на линию огня любого стрелка равновозможен, то вероятности этих гипотез до опыта равны Р (H 1) = Р (H 2) = Р (H 3) = 1/3.
В результате опыта наблюдалось событие А – после произведенных двух выстрелов мишень не поражена. Условные вероятности этого события равны
Р (А/H 1) = 0,7 × 0,7 = 0,49; Р (А/H 2) = 0,5 × 0,5 = 0,25; Р (А/H 3) = 0,2 × 0,2 = 0,04.
По формуле Бейеса для частного случая, когда вероятности гипотезы опыта равны между собой, находим вероятность гипотезы Н 1 после опыта:
Р (H 1/ A) = 
= 0,628
Пример 4. Найдите вероятность того, что в пяти независимых испытаниях событие появится: а) ровно 3 раза, б) не менее трех раз, в) не более трех раз г) хотя бы один раз, – если в каждом испытании вероятность появления этого события равна 0,8.
Решение. Так как число испытаний невелики, то для вычисления искомой вероятности воспользуемся формулой Бернулли: 
(k) = 
, где 
– число сочетаний из n элементов по k, q = 1 – p. В рассматриваемом случае:
а) вероятность появления события ровно 3 раза в 5 испытаниях равна
P 
(3) = 
= 
= 0,2048.
б) вероятность появления события не менее трех раз в 5 испытаниях равна
P (3) + P (4) + P (5)= 0,2048 + 
+ + 
= 0,2048 + 0,4096 + 0,3277 = 0,9421.
в) вероятность появления события не более 3 раз в 5 испытаниях равна
P (0)+ P (1) + P (2) + P (3)= 1 – P (4)– P (5)=
= 1 – 0,4096 – 0,3277 = 0,2629.
г) вероятность появления события хотя бы один раз в 5 испытаниях равна
P (1) + P (2) + P (3) + P (4) + P (5) = 1 – P (0) =
=1 – 
= 1 – 0,0003 = 0,9997.
При решении б) – г) использована теорема сложения вероятностей несовместных событий, а при решении в), г) – понятие противоположных событий, сумма вероятностей которых равна 1.
Пример 5. Вероятность попадания в цель у стрелка р = =0,8. Производится три выстрела. Построить ряд распределения случайной величины Х – числа попаданий в цель. Найдите математическое ожидание М [ X ] и дисперсию D [ X ].
Решение. Случайная величина Х может принимать значения: 0, 1, 2, 3. Вероятность того, что попаданий не будет р (х= 0) найдем по формуле Бернулли P (k) = 
, здесь p = 0,8, q = 1– p= 0,2, n = 3, k = 0.
p (x= 0) = 
= 
= 0,008.
Аналогично найдем p (x= 1) – в результате трех выстрелов будет одно попадание
p (x= 1)= 
= 
0,8 0,4 = 0,096;
p (x= 2)= 0,384; p (x= 3)=0,512.
Ряд распределения будет иметь вид
| x i | 0 | 1 | 2 | 3 | |
| p i | 0,008 | 0,096 | 0,384 | 0,512 |
Математическое ожидание М [ Х ] и дисперсию D [ Х ] определим по формулам
М [ X ] = 
хipi = 0,096 + 2×0,384 + 3×0,512 = 2,4;
D [ X ] = (хi -M [ X ])2 p i ; или
D [ X ] = M [ X 2] – (M [ X ])2.
Предварительно построим ряд распределения случайной величины X 2
| x i 2 | 0 | 1 | 4 | 9 | |
| p i | 0,008 | 0,096 | 0,384 | 0,512 |
M [ X 2] = 0,096 + 4×0,384 + 9×0,512 =6,24.
D [ X ]=6,24 – (2,4)2 = 0,48.
|
|
|
Пример 6. Дана плотность распределения
случайной величины Х. Найдите параметр а, функцию распределения случайной величины, математическое ожидание М [ X ], дисперсию D [ X ], вероятность выполнения неравенства
0 < X< 1.
Решение. Для определения параметра а воспользуемся основным свойством плотности распределения
f (x) dx = 1, т.к. при x 
[-1,1] плотность вероятности равна нулю, то получим равенство
dx = 1,
Вычислим интеграл
dx=
Поэтому 
, отсюда 
.
Функция распределения связана с функцией плотности соотношением
F (x) = 
f (x) dx.
1) х <- 1, F (x) = 0 dx=0;
2) -1 
x <1, F (x) = 
0 dx + 
3) х 1, F (x) = 
Таким образом, F (x) = 
Математическое ожидание М [ Х ] и дисперсию D [ Х ] определим по формулам
М [ X ] = х f (x) dx, D [ X ] = (х - M [ X ])2 f (x) dx.
В нашем случае
М [ X ]= 
d x= 
= 
D [ X ] = 
dх = dх – 
=
Вероятность выполнения неравенства 0 < X < 1 определим по формуле
Р (0 < X < 1) = 
f (x) dx = F (1) – F (0) = 1–1/2= 1/2.
Пример 7. Найдите вероятность попадания в данный интервал (15,25) нормально распределенной случайной величины, если известны ее математическое ожидание а = 20 и среднее квадратическое отклонение s = 5.
Решение. Для определения искомой вероятности воспользуемся формулой
Р (a< Х < b) = Ф 
- Ф 
.
Здесь Ф (х)= 
- функция Лапласа, значения которой определяются по таблице. Учитывая, что функция Ф (х) нечетная, получим
Р (15< Х <25) = Ф 
- Ф 
=
= Ф (1) - Ф (- 1) = 2 Ф (1)= 2× 0,34 = 0,68.
Пример 8. Определите доверительный интервал для оценки с надежностью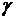 
=0,95 неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если выборочное среднее равно 
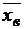= 14, объем выборки n = 25и генеральное среднее квадратическое отклонение 
= 5.
Решение. Требуется найти доверительный интервал
– 
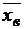< a < + (*)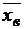
Здесь t – значение аргумента функции Лапласа Ф (t). при котором 2 Ф (t)= 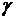. Все величины кроме t известны. Найдем t из соотношения Ф (t)= 0,95/2= 0,475.
|
|
|
По таблице функции Лапласа, зная ее значение, находим значение аргумента t =1,96. Подставив t =1,96, = 5,
n = 25, 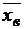= 14 в (*), окончательно получим искомый доверительный интервал
12,04< a < 15,96.
Приложения
Таблица изображений некоторых элементарных функций
| № п/п | 
| f (t) |
| 1 | 1/ p | 1 |
| 2 | 
| sin at |
| 3 | 
| cos at |
| 4 | 
| 
|
| 5 | 
| sh at |
| 6 | 
| ch at |
| 7 | 
| 
|
| 8 | 
| 
|
| 9 | 
| 
|
| 10 | 
| 
|
| 11 | 
| 
|
| 12 | 
| 
|
| 13 | 
| 
|
| 14 | 
| 
|
Таблица значений функции 
, 
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0,0 | 0.3989 | 3989 | 3989 | 3988 | 3986 | 3984 | 3982 | 3980 | 3977 | 3973 |
| 0,1 | 3970 | 3965 | 3961 | 3956 | 3951 | 3945 | 3939 | 3932 | 3925 | 3918 |
| 0,2 | 3910 | 3902 | 3894 | 3885 | 3876 | 3867 | 3857 | 3847 | 3836 | 3825 |
| 0,3 | 3814 | 3802 | 3790 | 3778 | 3765 | 3752 | 3739 | 3726 | 3712 | 3697 |
| 0,4 | 3683 | 3668 | 3653 | 3637 | 3621 | 3605 | 3589 | 3572 | 3555 | 3538 |
| 0,5 | 3521 | 3503 | 3485 | 3467 | 3448 | 3429 | 3410 | 3391 | 3372 | 3352 |
| 0,6 | 3332 | 3312 | 3292 | 3271 | 3251 | 3230 | 3209 | 3187 | 3166 | 3144 |
| 0,7 | 3123 | 3101 | 3079 | 3056 | 3034 | 3011 | 2989 | 2966 | 2943 | 2920 |
| 0,8 | 2897 | 2874 | 2850 | 2827 | 2803 | 2780 | 2756 | 2732 | 2709 | 2785 |
| 0,9 | 2661 | 2637 | 2613 | 2589 | 2565 | 2541 | 2416 | 2492 | 2468 | 2444 |
| 1,0 | 0.2420 | 2396 | 2371 | 2347 | 2323 | 2299 | 2275 | 2251 | 2227 | 2203 |
| 1,1 | 2179 | 2155 | 2131 | 2107 | 2083 | 2059 | 2036 | 2012 | 1989 | 1965 |
| 1,2 | 1942 | 1919 | 1895 | 1872 | 1849 | 1826 | 1804 | 1781 | 1758 | 1736 |
| 1,3 | 1714 | 1691 | 1669 | 1647 | 1626 | 1604 | 1582 | 1561 | 1539 | 1518 |
| 1,4 | 1497 | 1476 | 1456 | 1435 | 1415 | 1394 | 1374 | 1354 | 1334 | 1315 |
| 1,5 | 1295 | 1276 | 1257 | 1238 | 1219 | 1200 | 1182 | 1163 | 1145 | 1127 |
| 1,6 | 1109 | 1092 | 1074 | 1057 | 1040 | 1023 | 0906 | 0989 | 0973 | 0957 |
| 1,7 | 0940 | 0925 | 0909 | 0893 | 0878 | 0863 | 0848 | 0833 | 0818 | 0804 |
| 1,8 | 0709 | 0775 | 0761 | 0748 | 0734 | 0721 | 0707 | 0694 | 0681 | 0669 |
| 1,9 | 0656 | 0644 | 0632 | 0620 | 0608 | 0596 | 0584 | 0573 | 0562 | 0551 |
| 2,0 | 0.0540 | 0529 | 0519 | 0508 | 0498 | 0488 | 0478 | 0468 | 0459 | 0449 |
| 2,1 | 0440 | 0431 | 0422 | 0413 | 0404 | 0396 | 0387 | 0379 | 0371 | 0363 |
| 2,2 | 0355 | 0374 | 0334 | 0332 | 0325 | 0317 | 0310 | 0303 | 0297 | 0290 |
| 2,3 | 0283 | 0277 | 0270 | 0264 | 0258 | 0252 | 0246 | 0241 | 0235 | 0229 |
| 2,4 | 0224 | 0219 | 0213 | 0208 | 0203 | 0198 | 0194 | 0189 | 0184 | 0180 |
| 2,5 | 0175 | 0171 | 0167 | 0163 | 0158 | 0154 | 0151 | 0147 | 0143 | 0139 |
| 2,6 | 0136 | 0132 | 0129 | 0126 | 0122 | 0119 | 0116 | 0113 | 0110 | 0107 |
| 2,7 | 0104 | 0101 | 0099 | 0096 | 0093 | 0091 | 0088 | 0086 | 0084 | 0081 |
| 2,8 | 0079 | 0077 | 0075 | 0073 | 0071 | 0069 | 0067 | 0065 | 0063 | 0061 |
| 2,9 | 0060 | 0058 | 0056 | 0055 | 0053 | 0051 | 0050 | 0048 | 0047 | 0046 |
| 3,0 | 0.0044 | 0043 | 0042 | 0040 | 0039 | 0038 | 0037 | 0036 | 0035 | 0034 |
| 3,1 | 0033 | 0032 | 0031 | 0030 | 0029 | 0028 | 0027 | 0026 | 0025 | 0025 |
| 3,2 | 0024 | 0023 | 0022 | 0022 | 0021 | 0020 | 0020 | 0019 | 0018 | 0018 |
| 3,3 | 0017 | 0017 | 0016 | 0016 | 0015 | 0015 | 0014 | 0014 | 0013 | 0013 |
| 3,4 | 0012 | 0012 | 0012 | 0011 | 0011 | 0010 | 0010 | 0010 | 0009 | 0009 |
| 3,5 | 0009 | 0008 | 0008 | 0008 | 0008 | 0007 | 0007 | 0007 | 0007 | 0006 |
| 3,6 | 0006 | 0006 | 0006 | 0006 | 0005 | 0005 | 0005 | 0005 | 0005 | 0004 |
| 3,7 | 0004 | 0004 | 0004 | 0004 | 0004 | 0004 | 0003 | 0003 | 0003 | 0003 |
| 3,8 | 0003 | 0003 | 0003 | 0003 | 0003 | 0002 | 0002 | 0002 | 0002 | 0002 |
Таблица значений функции 
, 
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0,0 | 0,00000 | 00399 | 00798 | 01197 | 01595 | 01994 | 02392 | 02790 | 031888 | 03586 |
| 0,1 | 03983 | 04380 | 04776 | 05172 | 05567 | 05962 | 06356 | 06749 | 07142 | 07535 |
| 0,2 | 07926 | 08317 | 08706 | 09095 | 09483 | 09871 | 10257 | 10642 | 11026 | 11409 |
| 0,3 | 11791 | 12172 | 12552 | 12930 | 13307 | 13683 | 14058 | 14431 | 14803 | 15173 |
| 0,4 | 15542 | 15910 | 16276 | 16640 | 17003 | 17364 | 17724 | 18082 | 18439 | 18793 |
| 0,5 | 19146 | 19497 | 19847 | 20194 | 20540 | 20884 | 21226 | 21566 | 21904 | 22240 |
| 0,6 | 22575 | 22907 | 23237 | 23565 | 23891 | 24215 | 24537 | 24857 | 25175 | 25490 |
| 0,7 | 25804 | 26115 | 26424 | 26730 | 27035 | 27337 | 27637 | 27935 | 28230 | 28524 |
| 0,8 | 28814 | 29103 | 29389 | 29673 | 29955 | 30234 | 30511 | 30785 | 31057 | 31327 |
| 0,9 | 31594 | 31859 | 32121 | 32381 | 32639 | 32894 | 33147 | 33398 | 33646 | 33891 |
| 1,0 | 34134 | 34375 | 34614 | 34850 | 35083 | 35314 | 35543 | 35769 | 35993 | 36214 |
| 1,1 | 36433 | 36650 | 36864 | 37076 | 37286 | 37493 | 37698 | 37900 | 38100 | 38298 |
| 1,2 | 38493 | 38686 | 38877 | 39065 | 39251 | 39435 | 39617 | 39796 | 39973 | 40147 |
| 1,3 | 40320 | 40490 | 40658 | 40824 | 40988 | 41149 | 41309 | 41466 | 41621 | 41774 |
| 1,4 | 41924 | 42073 | 42220 | 42364 | 42507 | 42647 | 42786 | 42922 | 43056 | 43189 |
| 1,5 | 43319 | 43448 | 43574 | 43699 | 43822 | 43943 | 44062 | 44179 | 44295 | 44408 |
| 1,6 | 44520 | 44630 | 44738 | 44845 | 44950 | 45053 | 45154 | 45254 | 45352 | 45449 |
| 1,7 | 45543 | 45637 | 45728 | 45818 | 45907 | 45994 | 46080 | 46164 | 46246 | 46327 |
| 1,8 | 46407 | 46485 | 46562 | 46638 | 46712 | 46784 | 46856 | 46926 | 46995 | 47062 |
| 1,9 | 47128 | 74193 | 47257 | 47320 | 47381 | 47441 | 47500 | 47558 | 47615 | 47670 |
| 2,0 | 47725 | 47778 | 47831 | 47882 | 47932 | 47982 | 48030 | 48077 | 48124 | 48169 |
| 2,1 | 48214 | 48257 | 48300 | 48341 | 48382 | 48422 | 48461 | 48500 | 48573 | 48574 |
| 2,2 | 48610 | 48645 | 48679 | 48713 | 48745 | 48778 | 48309 | 48840 | 48870 | 48899 |
| 2,3 | 48928 | 48956 | 48983 | 49010 | 49036 | 49061 | 49086 | 49111 | 49134 | 49158 |
| 2,4 | 49180 | 49202 | 48224 | 49245 | 49266 | 49286 | 49305 | 49324 | 49343 | 49361 |
| 2,5 | 49379 | 49396 | 48413 | 49430 | 49446 | 49461 | 49477 | 49492 | 49506 | 49520 |
| 2,6 | 49534 | 49547 | 48560 | 49573 | 49585 | 49598 | 49609 | 49621 | 49632 | 49643 |
| 2,7 | 49653 | 49664 | 48674 | 49683 | 49693 | 49702 | 49711 | 49720 | 49728 | 49736 |
| 2,8 | 49744 | 49752 | 48760 | 49767 | 49774 | 49781 | 49788 | 49795 | 49801 | 49807 |
| 2,9 | 49813 | 49819 | 48825 | 49831 | 49836 | 49841 | 49846 | 49851 | 49856 | 49861 |
| 3,0 | 0,49865 | 3,1 | 49903 | 3,2 | 49931 | 3,3 | 49952 | 3,4 | 49966 | |
| 3,5 | 49977 | 3,6 | 49984 | 3,7 | 49989 | 3,8 | 49993 | 3,9 | 49995 | |
| 4,0 | 499968 | |||||||||
| 4,5 | 499997 | |||||||||
| 5,0 | 49999997 | |||||||||
