Равномерная сходимость

Понятие равномерной сходимости для несобственных интегралов, зависящих от параметра, столь же важно, как и для функциональных рядов.

Определение 2.8 Будем говорить, что интеграл (2.13) сходится равномерно на множестве Y, если его остаток равномерно стремится к нулю на этом множестве, то есть, если такое, что выполняется неравенство

(2.14)

Теорема 2.12 (критерий Коши) для того, чтобы интеграл (2.13) сходился равномерно на множестве Y, необходимо и достаточно выполнение следующего условия (условие Коши): , зависящее

только от , такое, что будет выполняться неравенство

(2.15)

Доказательство. Пусть интеграл (2.13) сходится равномерно на множестве Y. Тогда, взяв любое > 0, подберем так, чтобы для

любых А> А и у 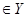выполнялось неравенство .

Возьмём любые и любое у 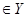. Тогда

и необходимость доказана.

Наоборот, если выполнено условие (2.15), то оно выполнено для любого фиксированного у 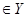. Но тогда по теореме 2.1 для любого фиксированного у интеграл (2.13) сходится, то есть, для каждого у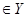

существует Поэтому, положив в (2.15) и устремив А" к +∞, получим для любого у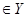

что означает равномерную на Y сходимость интеграла (2.13). ■

Теорема 2.13 (Вейерштрасс) Пусть f: [a, +∞) → R и для любых

А(> а) и у функция f интегрируема по Риману на отрезке [а; A].

Пусть g: [а; +∞) →R, для всех х [а; +∞), у выполняется

неравенство и сходится. Тогда интеграл (2.13) сходится равномерно (и абсолютно) на множестве Y.

Доказательство. По критерию Коши для несобственных интегралов

первого рода (см. 2.1) для любого > 0 найдётся такое, что для

любых будет выполняться неравенство Но тогда для любого у , для любых имеем:

Остаётся применить теорему 2.12..

Пример 2.11 Рассмотрим

Решение. Этот интеграл сходится равномерно на R, так как имеет место

Оценка а сходится. ■

Теорема 2.14 (Дирихле) Пусть функции f, g: [а; +∞) х Y→ R и

интегрируемы по Риману на [а; А] при любых А > а и у . Тогда

сходится равномерно на Y, если выполнены следующие два условия:

1) равномерно ограничен на [а; +∞), то есть, существует постоянная М такая, что для любых А> а и у

2)функция у(х, у) монотонно по х при каждом у и равномерно по у стремимся к нулю при х→+∞.

Доказательство. Доказательство этой теоремы такое же, как и доказательство теоремы 2.4, нужно лишь проследить, чтобы все оценки выполнялись равномерно по параметру.

По первому условию существует постоянная М такая, что для всех

A> а и у имеет место оценка:

(2.16)

По второму условию для любого > 0 найдётся (> а) такое, что

для любых А> и у выполнено

(2.17)

Возьмём и применим к интегралу вторую теорему о среднем значении (только на этот раз в общем виде, поскольку неизвестен знак g(х, у)), согласно которой найдётся А = А(у), А [А’, А”], такое, что

(2.18)

Оценим (2.18) с помощью (2.16) и (2.17).

для любого у из множества Y.

Используя критерий Коши, получаем требуемое утверждение. ■

Теорема 2.15 (Абель) Пусть функции f, g: [а; +∞) х Y→R и

интегрируемы по Риману на [а; А] при любых А > а и у . Тогда

сходимся равномерно на Y, если выполнены следующие два условия:

1) сходимся равномерно на множестве Y;

2)функция g(х, у) монотонна по х при каждом у и равномерно

по у ограничена, то есть, существует постоянная М такая, что

для всех х [а; +∞) и у .

Пример 2.12 Рассмотрим , где b> 0 постоянная, а параметр а удовлетворяет условию

Решение. Положим f(x,a)= sinax, g(x,a) Тогда

при х → +∞, и это условие (ввиду независимости функции g от а) вы-

полнено равномерно по а.

Так как оба условия признака Дирихле выполнены, то рассматриваемый интеграл сходится равномерно в указанной области. ■

Пример 2.13 Рассмотрим (a≥0)

Решение. Положим f(x, а) = , g(х, а) = . Так как

сходится равномерно по а (ввиду его отсутствия) по признаку Дирихле,

а функция , очевидно, монотонна по х и при х ≥ 0, у ≥0 ограничена,

то рассматриваемый интеграл сходится равномерно в указанной области

по признаку Абеля.■

2.4 Свойства несобственных интегралов, зависящих

От параметра

Изучим свойства несобственных интегралов первого рода, зависящих

от параметра, ограничившись простейшим случаем: множество Y есть

отрезок [с; d] вещественной оси. Введём обозначение

и докажем предварительно следующую лемму.

Лемма 2.1 Если интеграл (2.13) сходится равномерно на множестве Y

то последовательность функций

,() (2.19)

тоже равномерно сходится на множестве Y к функции I(y).

Теорема 2.16 Если функция f(x, у) определена и непрерывна на П ,

а интеграл (2.13) сходится равномерно на отрезке [с; d], мо функция

I(у), определяемая этим интегралом, непрерывна на [с; d].

Доказательство. По теореме 2.7 функции I (y) (n N) непрерывны на отрезке [с; d]. По лемме 2.1 последовательность функций I (y) (n N)

сходится равномерно на отрезке [с; d] к функции ‚I(у). Но тогда по теореме о пределе равномерно сходящейся последовательности непрерывных

функций функция I(у) непрерывна на отрезке [с; d]. ■

Следующая теорема является в некотором роде обратной к предыдущей.

Теорема 2.17 (Дини) Если функция f(x, у) непрерывна и неотрицательна П , а функция I(у), определяемая интегралом (2.13), непрерывна на отрезке [с; d], то интеграл (2.13) сходится равномерно на

отрезке [с; d].

Доказательство. По теореме 2.7 функции I (y) (n N) (см. (2.19))

непрерывны на отрезке [с; d]. Так как функция f(x, у) неотрицательна,

то последовательность функций I (y) (n N) монотонно не убывает.

Но тогда, поскольку предельная функция ‚I(у) этой последовательности тоже непрерывна, к ней можно применить теорему Дини для последовательностей, согласно которой последовательность I (у) сходится к

функции I(у) равномерно на отрезке [с; d]. Последнее означает, что для

любого > 0 найдётся номер n такой, что при n > n для всех у [с; d]

справедливо неравенство .

Положим и возьмём . Тогда, учитывая неотрицательность функции f(x, y), для всех у получаем:

и равномерная сходимость интеграла доказана. ■

Теорема 2.18 Если функция f(x, у) определена и непрерывна на

а интеграл (2.13) сходится равномерно на отрезке [с; d], то функция

I(у), определяемая этим интегралом, интегрируема на [с; d] и справедливо равенство

(2.20)

Доказательство. Снова рассмотрим последовательность I (у). По лемме 2.1 она сходится равномерно на отрезке [с; d] к функции I(у), а по теореме 2.8 функции последовательности интегрируемы на отрезке [с; d].

Тогда по теореме об интегрируемости предельной функции равномерно

сходящейся последовательности функция I(у) интегрируема на отрезке [с; d] и

Возможность изменения порядка интегрирования следует из той же

теоремы 2.8. ■

Теорема 2.19 Ecли функция f(x, у) непрерывна на множестве П и

имеет на нём непрерывную частную производную (х, y), интеграл (2.13) сходится, а интеграл

(2.21)

сходится равномерно на [с; d], то функция I(у) дифференцируема на отрезке [с; d] и справедливо равенство

(2.22)

Доказательство. Рассмотрим последовательность функций I (y). По

условию теоремы эта последовательность сходится на отрезке [с; d] (поскольку сходится интеграл (2.13)). По теореме 2.9 функции I (у) ( N)

дифференцируемы на отрезке [с; d], а по лемме 2.1 последовательность

производных I (у) сходится на этом отрезке равномерно. Но тогда по

теореме о дифференцируемости предельной функции равномерно сходящейся последовательности функция I(у) дифференцируема на отрезке

[с; d] и

■

В некоторых случаях бывает необходимо изменить порядок интегрирования, когда и переменная х и параметр у изменяются на бесконечных

промежутках. Пусть

Теорема 2.20 Пусть функция f(x, у) непрерывна и неотрицательна на К. Интегралы

(2.23)

оба сходятся и являются непрерывными функциями соответственно

на [с; +∞) и [а; +∞). Тогда равенство

(2.24)

справедливо при условии существования одного из повторных интегралов.

Доказательство. Допустим, что существует левый из интегралов в равенстве (2.24). Покажем, что в таком случае существует и правый интеграл, и что они равны. Для этого достаточно установить, что для любого

с > 0 найдётся А такое, что для любого А> А будет выполняться неравенство