Векторное произведение векторов

Определение. Векторным произведением векторов и называется вектор , удовлетворяющий следующим условиям:

1) , где  - угол между векторами и ,

2) вектор ортогонален векторам и

3) , и образуют правую тройку векторов. Обозначается: или . Свойства векторного произведения векторов:

 1) ;

2) , если  или = 0 или = 0;

3) (m ) = (m ) = m(  );

4) ( + ) =  +  ;

5) Если заданы векторы (xa, ya, za) и (xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами , то  =

6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .

Пример. Найти векторное произведение векторов и . = (2, 5, 1); = (1, 2, -3) .

Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0). (ед2).

 

Смешанное произведение векторов.

Определение. Смешанным произведением векторов , и называется число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов и . Обозначается или (, , ). Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах , и .

Свойства смешанного произведения:

1)Смешанное произведение равно нулю, если: а)хоть один из векторов равен нулю; б)два из векторов коллинеарны; в)векторы компланарны.

2)

3)

4)

5) Объем треугольной пирамиды, образованной векторами , и , равен

6)Если , , то

Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости. Найдем координаты векторов: Найдем смешанное произведение полученных векторов: , Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.

 

Вопрос 2: Первый замечательный предел:

Определение: Первым замечательным пределом называется предел

 

Теорема: Первый замечательный предел равен

Доказательство. Рассмотрим два односторонних предела и и докажем, что каждый из них равен 1. Тогда по теореме двусторонний предел также будет равняться 1.

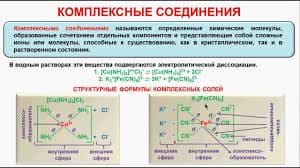
Итак, пусть (этот интервал - одно из окончаний базы ). В тригонометрическом круге (радиуса ) с центром построим центральный угол, равный 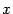, и проведём вертикальную касательную в точке пересечения горизонтальной оси с окружностью (). Обозначим точку пересечения луча с углом наклона 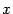с окружностью буквой , а с вертикальной касательной -- буквой ; через обозначим проекцию точки на горизонтальную ось.

Рис.2.27.Тригонометрический круг

 

Пусть - площадь треугольника , - площадь кругового сектора , а - площадь треугольника . Тогда очевидно следующее неравенство:

Заметим, что горизонтальная координата точки равна , а вертикальная - (это высота треугольника ), так что . Площадь центрального сектора круга радиуса с центральным углом равна , так что . Из треугольника находим, что . Поэтому Неравенство, связывающее площади трёх фигур, можно теперь записать в виде

Все три части этого неравенства положительны, поэтому его можно записать так:

или (умножив на ) так:

Предел постоянной 1 в правой части неравенства, очевидно, равен 1. Если мы покажем, что при предел в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части также будет равен 1.

Итак, осталось доказать, что . Сперва заметим, что , так как 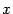равняется длине дуги окружности , которая, очевидно, длиннее хорды . Применяя теорему "о двух милиционерах" к неравенству

при , получаем, что

(2.3)

 

Простая замена переменной показывает, что и . Теперь заметим, что . Применяя теоремы о линейности предела и о пределе произведения, получаем:

(2.4)

 

Тем самым показано, что

Сделаем теперь замену ; при этом база перейдёт в базу (что означает, что если , то ). Значит,

но ( -- нечётная функция), и поэтому

Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы.

Доказанная теорема означает, что график функции выглядит так:

Рис.2.28.График

 

Билет 7:

Вопрос 1: Уравнение плоскости. Вывод и исследование:

Пусть в трехмерном пространстве задана прямоугольная система координат. Попробуем установить, какой вид может иметь уравнение плоскости. Для этого заметим, что все плоскости, перпендикулярные одной прямой, параллельны друг другу.

Определение 1: Любая прямая, перпендикулярная плоскости, называется нормалью к плоскости, а любой ненулевой вектор на такой прямой мы будем называть нормальным вектором плоскости.

Замечание 1: Из определения видно, что нормальный вектор у фиксированной плоскости определяется не однозначно. Все нормальные векторы одной плоскости коллинеарны друг другу и поэтому получаются один из другого умножением на число, отличное от нуля.

Для того чтобы из параллельных плоскостей выбрать одну, достаточно задать точку, через которую проходит эта плоскость. Итак, если у плоскости известны нормальный вектор и точка, через которую она проходит, то плоскость определена однозначно.

Теорема 1: Пусть вектор является нормальным вектором плоскости , проходящей через точку . Тогда уравнение

(1)

 

является уравнением плоскости .

Доказательство. Пусть -- некоторая точка плоскости (рис. 11.1). Иногда говорят "текущая точка" плоскости, так как предполагается, что ее координаты меняются и точка пробегает всю плоскость.

 

Рис.11.1.

 

Вектор лежит на плоскости . Следовательно, вектор ортогонален вектору n. Если же взять точку , не лежащую на плоскости , то вектор не будет ортогональным вектору n. Так как условием ортогональности двух векторов является равенство нулю их скалярного произведения, то условием того, что точка лежит в плоскости , является выполнение равенства

(2)

 

Выразив скалярное произведение в левой части этого равенства через координаты сомножителей по формуле, получим формулу (1).

Пусть r -- радиус-вектор текущей точки плоскости , -- радиус-вектор точки . Тогда уравнение (2) можно переписать в виде

Такое уравнение обычно называют векторным уравнением плоскости .

Раскроем скобки в уравнении (1). Так как точка - фиксированная, то выражение является числом, которое обозначим буквой . Тогда уравнение принимает вид

(3)

 

Такое уравнение называется общим уравнением плоскости. Еще раз отметим, что в этом уравнении хотя бы один из коэффициентов отличен от нуля, так как .

Верно и обратное утверждение:

Теорема 2: Всякое уравнение (3), в котором , является уравнением плоскости, ортогональной вектору .

Доказательство: Условие означает, что хотя бы одно из чисел , отлично от нуля. Пусть это будет, например, число 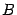. Преобразуем уравнение (3) следующим образом:

По теореме 1 такое уравнение является уравнением плоскости с нормальным вектором n, проходящей через точку .

Теорема 3: позволяет написать уравнение плоскости, если известна точка этой плоскости и вектор, ортогональный плоскости. Однако, довольно часто встречаются задачи, где требуется получить уравнение плоскости, если известна точка, лежащая на ней, и два неколлинеарных вектора, лежащих или, что то же самое, параллельных плоскости. Покажем на примере, как решается такая задача.

 

Вопрос 2: Второй замечательный предел:

Определение: Вторым замечательным пределом называется предел

Число , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число часто называют основанием натуральных логарифмов.

Теорема: Второй замечательный предел существует. Его значение - число, лежащее между и .

Лемма: Пусть и - натуральное число. Тогда имеет место формула

Заметим, что в дроби очевидно, сокращаются все сомножители в числителе и знаменателе, так что эта дробь равна 1. Аналогично, в предыдущем (не выписанном) слагаемом после сокращения получается коэффициент, равный , в третьем справа слагаемом -равный , и т. д. Таким образом, коэффициенты в слагаемых, стоящих на одинаковых местах, считая слева и справа от края формулы, совпадают.

Доказательство. Оказывать утверждение леммы будем по индукции по параметру . При формула, очевидно, верна:

Заметим, что при и  ормула также хорошо известна:

и

Предположим, что она верна для , и докажем, что тогда она верна и при . Действительно,

При этом в квадратных скобках получается:

и так далее, то есть как раз то, что должно получиться в качестве коэффициентов формулы бинома Ньютона при .

Доказательство теоремы. Рассмотрим последовательность и применим к формулу бинома Ньютона при и . Получим

Покажем, что последовательность ограничена сверху. Для этого заменим все дроби , ,..., на 1. Все эти дроби меньше 1, так что сумма в правой части формулы увеличится:

Далее, заменим все числа в знаменателях этих слагаемых на 2; от этого правая часть ещё увеличится. Получим:

В правой части получилась сумма членов геометрической прогрессии. Она равна

Поэтому

что и означает ограниченность последовательности сверху числом 3.

Покажем теперь, что последовательность не убывает. Действительно, запишем формулу в виде

В аналогичной формуле, написанной для вместо , во-первых, увеличится каждое из выражений в круглых скобках (так как вычитаемое уменьшится) и, значит, увеличатся все слагаемые, содержащие такие скобки. Во-вторых, число слагаемых увеличится на одно: добавится положительное слагаемое

Следовательно, при росте номера члены последовательности строго возрастают: при всех .

Применим теперь к возрастающей ограниченной сверху последовательности теорему о пределе монотонной ограниченной функции и получим, что существует предел

причём число не больше постоянной 3, ограничивающей последовательность. Осталось заметить, что . Так как все последующие члены ещё больше, то и предел , на основании теоремы о переходе к пределу в неравенстве, не меньше числа , что и завершает доказательство теоремы.

Замечание:  Можно также показать, что

однако строгое доказательство достаточно тяжело, и мы его здесь пропускаем.

В формуле можно сделать замену , при этом база 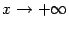перейдёт в базу , и мы получим

Билет 8:

Вопрос 1: Условия параллельности и перпендикулярности плоскостей:

 

 

Угол между двумя плоскостями в пространстве j  связан с углом между нормалями к этим плоскостям j₁ соотношением:

 j = j₁  или j = 180⁰ - j₁, т.е. cos j = cosj₁.

 

Определим угол j₁. Известно, что плоскости могут быть заданы соотношениями:

, где

(A1, B1, C1), (A2, B2, C2). Угол между векторами нормали найдем из их скалярного произведения:

.

Таким образом, угол между плоскостями находится по формуле:

Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.

На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.

Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:

.

Плоскости параллельны, векторы нормалей коллинеарны: // .Это условие выполняется, если: .

 

Вопрос 2: Неопределенности и способы их раскрытия:

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

1. ,

2. ,

3. 0 / 0,

4. 00,

5. ,

6. ,

7.

По таким выражениям сложно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

 

Правило Лопиталя: раскрытия неопределенностей 0/0 и ∞/∞

Ранее мы познакомились с примерами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞. Сейчас рассмотрим новое правило раскрытия этих неопределенностей.

Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или . Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

 

(1)

 

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

 

Билет 9:

Вопрос 1: Общее уравнение прямой на плоскости. Различные способы задания прямой:

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А² + В² ¹ 0. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:- C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат- А = 0, В ¹ 0, С ¹ 0 { By + C = 0}- прямая параллельна оси Ох- В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – прямая параллельна оси Оу- В = С = 0, А ¹ 0 – прямая совпадает с осью Оу- А = С = 0, В ¹ 0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.